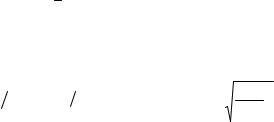
Решение этого уравнения удобно находить численно или графически, так как оптимум δ по η довольно пологий.

Теперь, зная δгл,ψ,ηopt , находим толщину δ из (5.16), а для

определения расстояния между ребрами воспользуемся условием местной устойчивости участка оболочки между ребрами:

Теперь h = ηoptl ; δисх = ψδ и все размеры отсека определены. Да-

лее необходимо провести конструкторское проектирование отсека, после чего в рамках проверочного расчета найти коэффициенты запаса устойчивости отсека и его элементов.

5.3.Шпангоуты

Вотсеках, нагруженных внешним давлением, применяют нормальные, силовые и стыковочные шпангоуты.

Нормальный шпангоут придает отсеку заданную геометрическую форму, а также делит его на части, повышая жесткость и критическое давление потери устойчивости.

Силовой шпангоут, предназначенный для крепления грузов внутри отсека, выполняет одновременно и функции нормального шпангоута.

Стыковочные шпангоуты имеются в отсеке всегда, так как обеспечивают соединение со смежными отсеками ракеты. В отличие от нормальных шпангоутов, на силовой и стыковочный шпангоуты действует нагрузка, перпендикулярная их плоскости.

5.3.1.Нормальный шпангоут

Шпангоут представляет собой кольцо с различной формой поперечного сечения. Работает на погонную нагрузку, действующую в его плоскости, которую через внешнее давление можно выразить так: q = ppl , где l – расстояние между шпангоутами

(рис. 28); pp = fp – расчетное внешнее давление.

Под действием этой нагрузки шпангоут сжимается, а напряжения, возникшие в его сечении, определяются из условия равновесия одной четвертой части кольца шпангоута в проекции на

63

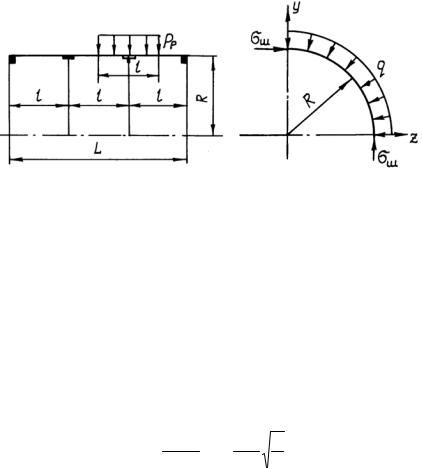
ось у (рис. 29). Имеем qR = σшFш , откуда напряжение в шпанго-

уте σш, выраженное через площадь его сечения Fш и нагрузку q, равно: σш = qRFш .

Полученное в результате проектировочного расчета значение площади шпангоута должно удовлетворять условиям прочности и устойчивости. При проверке на прочность сравниваем напряжения в шпангоуте с пределом текучести, а коэффициент запаса прочности равен: η1 = σ0,2 σш ≥1 .

Далее шпангоут проверяется на общую и местную устойчивость, а коэффициент запаса устойчивости η2 = qкр 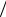q ≥1, где

критическая погонная нагрузка, определяемая с учетом подкрепляющего влияния примыкающей к шпангоуту оболочки, рав-

на [30]:

Чтобы определить момент инерции сечения шпангоута, необходимо знать его форму или коэффициент k в выражении, свя-

зывающем момент инерции и площадь шпангоута: J ш = kFш2 .

Задаваясь конфигурацией сечения, можно подобрать толщину и размеры его элементов по известным площади сечения и условиям местной устойчивости криволинейных пластинок, из которых состоит профиль шпангоута.

64

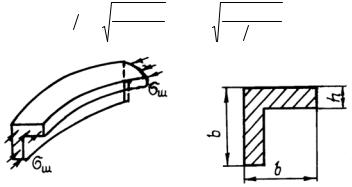
Рассмотрим порядок определения размеров сечения шпангоута на примере равнобокого уголкового профиля (рис. 30). В этом случае два неизвестных – h, b и два условия для их определения:

Fш = h2 (2bh −1) σш = 0,3825E(hb)2 ,

из которых

Рис. 30. Сечение уголкового профиля

Окончательные размеры b и h уточняются на стадии конструкторского проектирования.

5.3.2. Силовой шпангоут

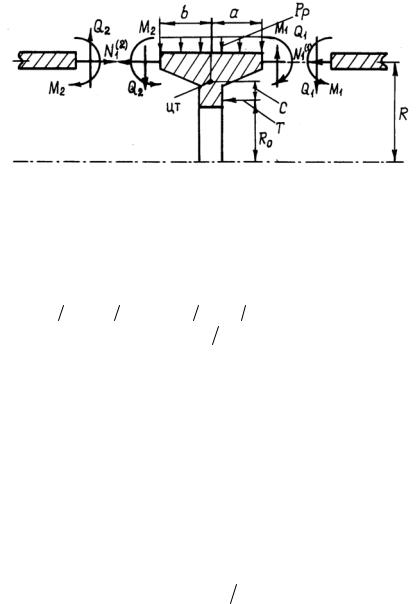
Основной нагрузкой, кроме внешнего давления, воспринимаемой силовым шпангоутом, является осевая погонная сила Т, действующая на него со стороны закрепленного груза (рис. 31, где показаны все погонные силы и моменты, действующие на шпангоут со стороны примыкающих к нему оболочек). Если принять в качестве положительных направление вверх для погонных сил, а вращение против часовой стрелки – для погонных моментов, то погонная сила, действующая на шпангоут, и погонный момент равны соответственно:

q =Q1 −Q2 − pp (a +b) ,

(5.17)

mшп = M 2 − M1 −T c +Q1 a +Q2 b .

Теперь из-за поворота вокруг центра тяжести сечения наибольшие напряжения возникают на его краях и определяются по формуле

65

Рис. 31. Схема нагружения силового шпангоута

где верхний знак и xi = a относятся к правому краю шпангоута, а нижний знак и xi = b – к левому. Перемещение центра тяжести

шпангоута wшп в направлении, перпендикулярном оси отсека, после приравнивания тангенциальной деформации, определенной из геометрических и физических уравнений, т.е.

Для определения угла поворота шпангоута составим сумму моментов относительно оси y для одной четвертой части шпангоута, на которую действуют погонный момент mшп (рис. 32) и напряжения σм по его сечению. Так как напряжения по сечению шпангоута переменные, то условие равновесия выделенной части имеет вид

Но напряжения в любой точке шпангоута, создаваемые моментом, равны: σм = (Eθшп R)η, поэтому (5.20) запишем так:

Eθшп R ∫η2dF = mшпR ,

66

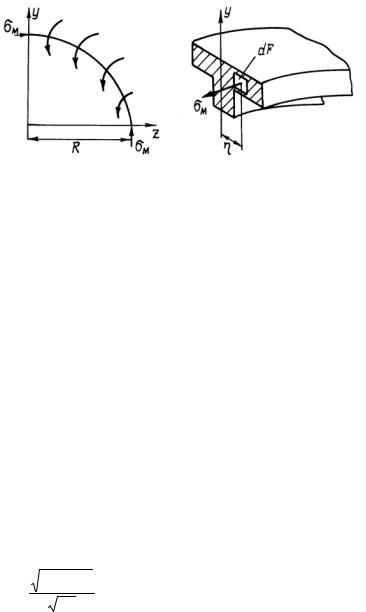
m шп

Рис. 32. Схема нагружения силового шпангоута погонным моментом

где J y = ∫ η2dF – момент инерции сечения шпангоута относи-

Fшп

тельно центральной y, перпендикулярной оси симметрии отсека. Таким образом, напряжения в любой точке шпангоута определяются по формуле (5.18), если известны q и mшп, которые, в свою очередь, зависят, как это следует из (5.17), от краевых перерезывающих сил Q1 , Q2 и моментов М1 и М2. Для их нахождения необходимо воспользоваться условиями совместности перемещений и углов поворота шпангоута и оболочек, примыкающих

к нему слева и справа. Для правого края

ные погонные усилия в сечениях оболочки. Решая систему урав-

67