3.3 Определение напряжений в обечайке
Определим расчётное окружное напряжение в месте стыка обечайки и нижнего днища по формуле:
Меридиональные расчётные напряжения определяются по формуле:
где
– расчетное значение осевой силы,
–
расчетное
значение изгибающего момента,
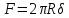– площадь
сечения бака,
– момент
инерции сечения относительно оси х,
y – расстояние до расчетного сечения.
Так
как максимальное и минимальное
меридиональное напряжение будут в
сечениях с координатами
,
получим:
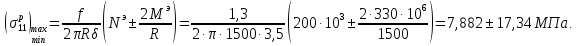
Следовательно
Максимальное расчётное касательное напряжение:
Эквивалентное напряжение в обечайке определяется по формуле
.
Расчет
выполним для четырех характерных точек
сечения I-I,
изображенных на рисунке 3.4, в которых
различаются
и
.
В
точке 1, где
имеем
В
точках 2 и 4, где
имеем
В
точке 3, где
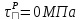имеем
Запас прочности по обечайке:
Рисунок 3.4 – Расчётные точки в сечении I-I
3.4 Расчёт бака на устойчивость
Критическое напряжение, соответствующее потере устойчивости бака:
;
Здесь
общий коэффициент
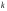определяется как:
.
Коэффициент устойчивости, получаемый в предположении о равномерности сжатия бака по сечению и отсутствия внутреннего давления, подсчитывается по формуле:
Коэффициент, учитывающий влияние внутреннего давления в баке, определяется по формуле:
где
Тогда
Коэффициент, учитывающий неравномерность распределения сжимающих напряжений по сечению бака, обусловленную действием изгибающего момента:
.
Эту формулу так же можно записать в другом виде:
Тогда получаем:
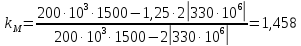
Коэффициент,
учитывающий влияние пластических
деформаций материала бака принимаем
для первого приближения, т.е. считаем,
что оболочка работает в упругой области.
Общий коэффициент устойчивости в первом приближении:
.
Критическое напряжение, соответствующее потери устойчивости бака:
;
Для первого приближения имеем:
Интенсивность напряжений определяется по формуле:
,
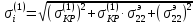где
Тогда интенсивность напряжений будет равна:
В первом приближении секущий и касательный модули равны модулю упругости материала. Предполагается, что бак работает в упругой области:
Найдем секущий и касательный модули во втором приближении по формулам:
Здесь
А,
В, D, G параметры
аппроксимации диаграммы растяжения
материала
:
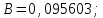
Найдем
значение деформации
:
Секущий и касательный модули материала будет равен:
Коэффициент,
учитывающий влияние пластических
деформаций материала бака
:
.
Критическое напряжение во втором приближении:
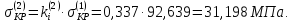
Вычисления
проводятся далее до тех пор, пока
в двух соседних приближения не будут
отличаться менее чем на два процента.
В результате вычислений с помощью
программы SIGMAcr.exe
получаем
.
Результат работы программы приведен на странице 59.
Критическое касательное напряжения:
,
где
где
– расстояние между шпангоутами
,
где
- критическое внешнее избыточное
давление.
.
.
В
первом приближении
.
Тогда критическое напряжение в первом напряжении будет равно:
Интенсивность напряжений в первом приближении:
,
,
где
Тогда интенсивность напряжений в первом приближении будет равна:
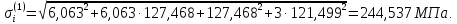
Найдем
значение деформации
:
В первом приближении секущий и касательный модули равны модулю упругости материала. Предполагается, что бак работает в упругой области:
Найдем секущий и касательный модули во втором приближении по формулам:
Здесь
А,
В, D, G параметры
аппроксимации диаграммы растяжения
материала
:
.
Секущий и касательный модули материала будет равен:
Коэффициент,
учитывающий влияние пластических
деформаций материала бака
:
.
Критическое напряжение во втором приближении:
Таким
образом проводятся вычисления далее
до тех пор, пока
в двух соседних приближения не будут
отличаться менее чем на два процента.
В результате вычислений с помощью
программы TAUcr.DAT получаем
.
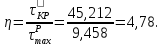
Результат работы программы приведен на странице 59 .
РЕЗУЛЬТАЕЫ ВЫЧИСЛЕНИЙ
Критическое напряжение SIGMAcr (в МПа)
3.3938D+01
Ko,Kp,Km
1.8443D-01 2.1707D+00 1.4583D+00
Ki(I),I-номер приближения
1.0000D+00 3.3680D-01 3.4764D-01 3.5477D-01 3.5929D-01
3.6208D-01 3.6379D-01 3.6482D-01 3.6543D-01 3.6580D-01
3.6602D-01 3.6616D-01 3.6623D-01 3.6628D-01 3.6631D-01
3.6633D-01 3.6634D-01 3.6634D-01 3.6634D-01 3.6635D-01
3.6635D-01 3.6635D-01 3.6635D-01 3.6635D-01 3.6635D-01
3.6635D-01 3.6635D-01 3.6635D-01 3.6635D-01 3.6635D-01
SIGMAcr(I) (в МПа),I-номер приближения
9.2638D+01 3.1200D+01 3.2205D+01 3.2865D+01 3.3284D+01
3.3543D+01 3.3700D+01 3.3796D+01 3.3853D+01 3.3887D+01
3.3908D+01 3.3920D+01 3.3927D+01 3.3931D+01 3.3934D+01
3.3936D+01 3.3936D+01 3.3937D+01 3.3937D+01 3.3938D+01
3.3938D+01 3.3938D+01 3.3938D+01 3.3938D+01 3.3938D+01
3.3938D+01 3.3938D+01 3.3938D+01 3.3938D+01 3.3938D+01
ИСХОДНЫЕ ДАННЫЕ
R,DELTA (в мм)
1.5000D+03 3.5000D+00
E,SIGMAp(в МПа)
6.8000D+04 1.2000D+02
A,B,C,D,G
1.2406D+00 9.5603D-02 1.0800D-02 5.9312D-02 6.8120D-01
Nэ(в кН),Mэ(в кН*м),Pэ(в МПа)
2.0000D+02 3.3000D+02 2.9740D-01
SIGMAcr2
3.1198D+01
РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ
Критическое касательное напряжение TAUcr (в МПа)
4.5212D+01
TAUcr0(в МПа)
3.7246D+01
Kp
3.2643D+00
Ki(I),I-номер приближения
1.0000D+00 2.5545D-01 2.9577D-01 3.2887D-01 3.5055D-01
3.6220D-01 3.6770D-01 3.7011D-01 3.7114D-01 3.7156D-01
3.7174D-01 3.7182D-01 3.7185D-01 3.7186D-01 3.7186D-01
TAUcr(I) (в МПа),I-номер приближения
1.2158D+02 3.1058D+01 3.5960D+01 3.9985D+01 4.2620D+01
4.4037D+01 4.4706D+01 4.4999D+01 4.5123D+01 4.5175D+01
4.5197D+01 4.5206D+01 4.5210D+01 4.5211D+01 4.5212D+01
ИСХОДНЫЕ ДАННЫЕ
R,DELTA,L(в мм)
1.5000D+03 3.5000D+00 8.0000D+02
E,SIGMAp(в МПа)
6.8000D+04 1.2000D+02
A,B,C,D,G
1.2410D+00 9.5600D-02 1.0800D-02 5.9310D-02 6.8120D-01
Nэ(в кН),Pэ(в МПа),Pcr(в МПа)
2.0000D+02 2.9740D-01 3.0800D-02
TAUcr2
3.1048D+01