
- •1 Вычисление внутренних усилий в сечениях корпуса ла
- •Определение угла атаки и величины скоростного напора
- •Расчет продольных аэродинамических нагрузок
- •Определение продольной перегрузки
- •Определение осевой силы
- •Определение продольной аэродинамической силы
- •Определение силы, обусловленной массой конструкции
- •Определение силы, обусловленной давлением наддува
- •Определение силы, обусловленной влиянием массы топлива
- •Определение силы, обусловленной тягой двигателя
- •Определение осевой силы
- •Проверка правильности построения эпюр
- •1.5 Расчет нормальной перегрузки и величины углового ускорения
- •Построение эпюр m и q по длине летательного аппарата
-
Определение осевой силы
Значение осевой силы в произвольном сечении «ξ» можно представить в виде суммы:
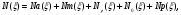
где
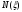 -
осевая сила в сечении «ξ»;
-
осевая сила в сечении «ξ»;
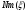 -
вклад в осевую силу массы конструкции;
-
вклад в осевую силу массы конструкции;
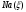 -
продольная аэродинамическая сила;
-
продольная аэродинамическая сила;
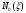 -
влияние давления наддува баков;
-
влияние давления наддува баков;
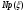 -
вклад тяги двигателя;
-
вклад тяги двигателя;
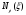 -
влияние массы топлива.
-
влияние массы топлива.
-
Определение продольной аэродинамической силы
Продольная аэродинамическая сила отсеченной части конструкции может быть определена по формуле:
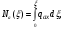
где
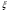 - координата, отчитывающаяся от носка
ракеты;
- координата, отчитывающаяся от носка
ракеты;
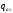 -
полная погонная аэродинамическая
нагрузка на корпус ЛА.
-
полная погонная аэродинамическая
нагрузка на корпус ЛА.
Полная погонная аэродинамическая нагрузка определяется по формуле:
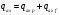 ,
,
где
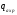 - продольная погонная нагрузка, вызванная
силами давления на боковую поверхность
ЛА;
- продольная погонная нагрузка, вызванная
силами давления на боковую поверхность
ЛА;
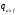 -
продольная погонная нагрузка от сил
трения.
-
продольная погонная нагрузка от сил
трения.
Нагрузка
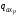 в
случае конического тела определяется
по формуле:
в
случае конического тела определяется
по формуле:
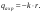
Коэффициент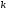 определяется по формуле:
определяется по формуле:
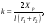
где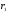 и
и
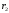 - радиусы оснований конического участка,
а
- радиусы оснований конического участка,
а
 - текущий радиус.
- текущий радиус.
В
точке 0 продольная погонная нагрузка,
вызванная силами трения на боковую
поверхность
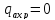 .
.
В сечении шпангоута № 1, изображенного на рисунке 5, погонная нагрузка, вызванная силами трения на боковую поверхность будет равна:
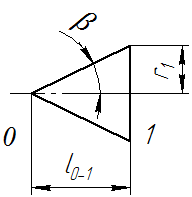
Рисунок 6 – Участок 0-1
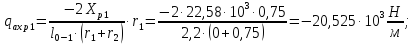
В сечениях шпангоутов № 4 и №7, изображенных на рисунке 6, погонная нагрузка, вызванная силами трения на боковую поверхность будет равна:
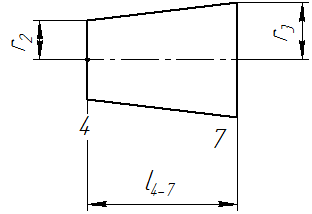
Рисунок 7 – Участок 4-7
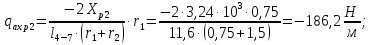
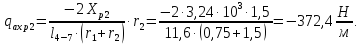
В сечениях шпангоутов № 9 и №10, изображенных на рисунке 7, погонная нагрузка, вызванная силами трения на боковую поверхность будет равна:
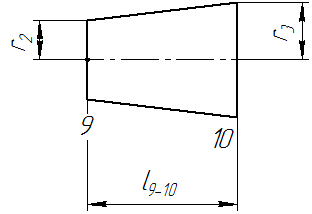
Рисунок 8 – Участок 9-10
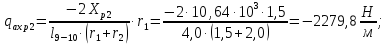
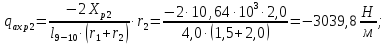
Погонная
нагрузка
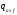 ,
вызванная поверхностным трением,
определяется по формуле:
,
вызванная поверхностным трением,
определяется по формуле:
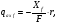
где F – половина площади продольного сечения летательного аппарата;
 -
текущий радиус .
-
текущий радиус .
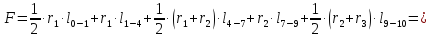
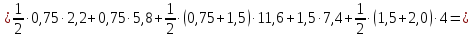
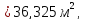
где
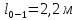 – длина участка 1-4,
– длина участка 1-4,
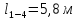 – длина
участка 1-4,
– длина
участка 1-4,
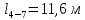 – длина
участка 4-7,
– длина
участка 4-7,
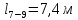 – длина
участка 7-9,
– длина
участка 7-9,
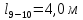 – длина
участка 9-10,
– длина
участка 9-10,
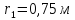 – радиус
основания конуса,
– радиус
основания конуса,
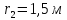 – радиус
основания конуса,
– радиус
основания конуса,
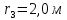 – радиус
основания конуса.
– радиус
основания конуса.
Тогда
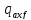 на участке 1-4 будет равна
на участке 1-4 будет равна
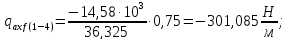
На участке 7-9:
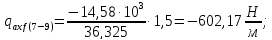
В сечении 10:
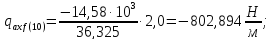
Складывая
значения
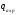 и
и
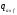 ,
получим полную погонную аэродинамическую
нагрузку на корпус летательного аппарата.
,
получим полную погонную аэродинамическую
нагрузку на корпус летательного аппарата.
Эпюры
погонных нагрузок
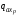 ,
,
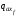 ,
а также результат их суммирования
представлены на рисунке 9.
,
а также результат их суммирования
представлены на рисунке 9.
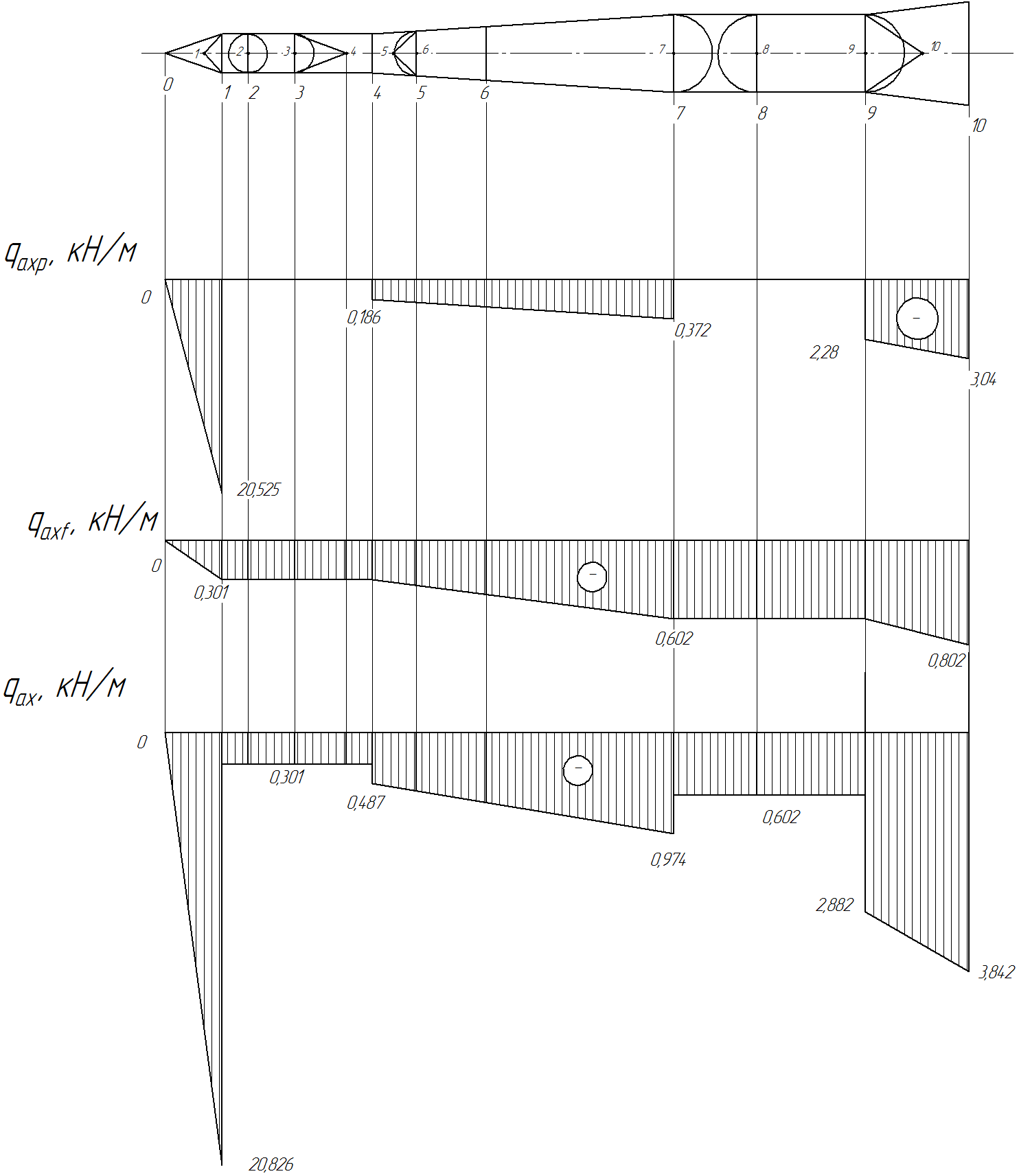
Рисунок 9 – Эпюры погонных нагрузок
Продольная
аэродинамическая сила
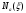 представлена
на рисунке 10.
представлена
на рисунке 10.
-
Определение силы, обусловленной массой конструкции
Величина силы, обусловленной массой конструкции отсеченной части, определяется по формуле :
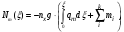
где
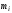 - масса i-го
сосредоточенного груза;
- масса i-го
сосредоточенного груза;
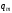 -
погонная масса конструкции,
-
погонная масса конструкции,
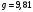 м/с2
– ускорение свободного падения.
м/с2
– ускорение свободного падения.
Эпюра
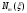 представлена на рисунке 10.
представлена на рисунке 10.
-
Определение силы, обусловленной давлением наддува
Величина силы, обусловленной давлением наддува в баках, определяется по формуле:
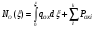 ,
,
где
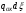 - дополнительная осевая сила от давления
наддува. Для цилиндрических баков
- дополнительная осевая сила от давления
наддува. Для цилиндрических баков
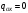 ;
;
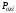 -
усилия, передаваемые на корпус от днищ
баков и обусловленные действием давления
наддува.
-
усилия, передаваемые на корпус от днищ
баков и обусловленные действием давления
наддува.
Для передних днищ эти силы определяются по формуле:
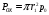 ,
,
а для задних – по формуле:
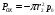 ,
,
где
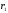 и
и
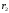 - радиусы оснований баков.
- радиусы оснований баков.
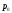 -
давление наддува в баке.
-
давление наддува в баке.
Так как все баки имеют цилиндрическую форму, усилия на переднем и заднем шпангоутах будут одинаковыми, отличаясь лишь знаком.
В баках II ступени давление наддува:
Горючего: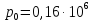 Па,
Па,
Окислителя: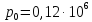 Па,
Па,
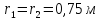 .
.
Тогда получаем:
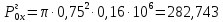 кН;
кН;
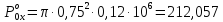 кН.
кН.
В баках I ступени давление наддува:
Горючего: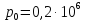 Па,
Па,
Окислителя: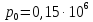 Па.
Па.
Для
бака окислителя
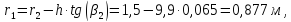
где h = 9,9 м – длина конической части бака,
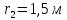 – радиус
основания бака.
– радиус
основания бака.
Тогда величина силы, обусловленной наддувом в баке будет равна:
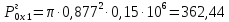 кН;
кН;
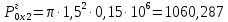 кН.
кН.
Радиус бака окислителя будет равен:
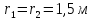 .
.
Тогда получим:
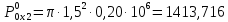 кН.
кН.
Эпюра
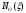 представлена на рисунке 10.
представлена на рисунке 10.
