Файловый архив студентов. Файловый архив студентов.
1304 вуза, 5158 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
ikot.chulakov@gmail.com Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Самарский национальный исследовательский университет им. ак. С.П. Королёва (бывш. СГАУ, СамГУ)
Предмет:
Вариационное исчисление
Файл:
Вариационные методы Старинова / Лекция 5.ppt
Скачиваний:
38
Добавлен:
12.07.2020
Размер:
659.46 Кб
Скачать
☆
►Содержание►

Самарский государственный аэрокосмический университет

Лекция 5. Изопериметрические задачи. Задача Дидоны.

Задача на условный экстремум

О. Л. Старинова

Кафедра Космического машиностроения

2015 г.

Изопериметрическая задача

Задача отыскания среди всех кривых y(x), удовлетворяющих условиям

y x1 y1;

(5.1)

 

y2 ;

 

y x2

 

кривой доставляющей экстремум функционалу (целевой функционал)

x2

 

 

(5.2)

 

J ( y) F

 

x, y, y dx extr

 

x1

 

 

 

при выполнении условия (условие связи)

 

x2

 

 

(5.3)

K ( y) G(x, y(x), y (x))dx l

 

 

 

 

x1

 

 

 

называется изопериметрической задачей.

Первоначально под изопериметрической задачей понималась частная задача (задача Дидоны): среди всех замкнутых кривых, имеющих заданную длину, найти ту, которая охватывает наибольшую площадь (задача с фиксированным периметром).

Теорема о необходимом условии экстремума для изопериметрической задачи

Th 1. Если кривая y(x) дает экстремум функционалу (5.2), удовлетворяет условиям (5.1) и (5.3) и не является экстремалью функционала (5.3), то существует такая постоянная , что эта кривая является экстремалью функционала

x2

F G dx extr

 

 

(5.4)

 

x1

 

 

Доказательство

Пусть кривая y(x) удовлетворяет всем условиям теоремы. Возьмем в интервале x [x1, x2] две произвольные точки a и b и придадим y(x)

приращение y= ay+ by , отличное от нуля лишь в окрестностях этих

точек. Соответствующее приращение J функционала можно представить в виде

 

 

F

 

d

 

F

 

 

 

 

 

 

 

 

 

F

 

d

 

F

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

J

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

(5.5)

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

a

 

 

y

 

 

 

 

 

 

 

 

b

 

 

 

dx

y

 

x a

 

 

 

 

 

 

 

 

dx

y

 

x b

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Теорема о необходимом условии экстремума для изопериметрической задачи

где x2

x2

a a y dx,

b b y dx

x1

x1

и 1, 2 0 при a, b 0 .

Потребуем теперь, чтобы проварьированная кривая y1 x y x a y b y

удовлетворяла условию (5.3).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариацию функционала

можно представить в аналогичном виде

 

 

 

 

 

 

 

 

 

 

G

 

d

G

 

 

 

 

 

 

G

 

d

G

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

K K y1 K y

 

 

 

 

 

 

 

 

1

a

 

 

 

 

 

 

 

 

 

2

 

b 0

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

y

 

x а

 

 

 

 

 

dx

y

 

x b

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Выберем теперь точку b так, что

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

G

 

d

G

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(5.6)

 

 

dx

y

 

x b

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Теорема о необходимом условии экстремума для изопериметрической задачи

Такая точка существует, так как по условию теоремы y(x) не является экстремалью функционала – условия связи. При таком выборе точкиK=0 можно придать вид

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

G

 

 

d

G

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

b

 

 

 

dx

 

 

 

 

 

x a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

G

 

 

d

G

 

 

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

y

 

x b

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Подставим (5.7) в (5.4), отбросив бесконечно малые

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

G

 

 

d

 

G

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

F

 

d

 

 

F

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

F

 

d

 

F

 

 

 

 

 

J

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

G

 

 

d

 

G

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

dx

y

 

 

 

 

 

 

 

 

 

 

dx

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x b

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

dx y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x b

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(5.7)

(5.8)

Теорема о необходимом условии экстремума для изопериметрической задачи

Обозначим

 

 

F

 

d

 

F

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

dx

y

 

 

 

x b

(5.9)

 

 

 

 

G

 

d

 

G

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

dx

y

 

x b

 

 

 

 

 

 

подставим (5.9) в (5.8) получим

 

 

 

 

 

 

 

 

 

 

 

F

 

d F

 

 

 

 

G

 

d

G

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

J

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

(5.10)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

dx

y

 

 

x a

 

 

dx

y

 

 

x a

 

 

 

 

 

 

 

 

 

 

Так как вариация функционала должна быть равно нулю, то из (5.10) следует, что экстремум функционала J при выполнении изопериметрического условия соответствует экстремуму функционала

x2

F G dx extr Что и требовалось доказать.

x1

Пример 5.1 Решение вариационной задачи с изопериметрическим условием

Найти кривую в верхней полуплоскости, проходящую через точки (-1; 0) и (1; 0) , имеющую заданную длину и охватывающую вместе с отрезком [-1; 1] максимальную площадь.

Мы ищем функцию y(x) для которой y(-1)=0, y(1)=0, интеграл

1

J ( y) ydx max,

1

принимает максимальное значение и выполняется условие

1

K y 1 y 2 dx

1

Мы имеем, таким образом изопериметрическую задачу.

Пример 5.1 Решение вариационной задачи с изопериметрическим условием

По Th 1 составляет функционал

J y K y

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

y 1 y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

и пишем для него уравнение Эйлера

 

 

 

 

 

 

 

 

 

 

 

 

d

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

1 y

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

отсюда находим

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

2

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

x c

 

 

x

 

 

 

 

 

c1,

 

 

 

 

 

 

 

 

 

x c

, y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

2

 

1 y

 

 

 

 

 

1 y

 

 

 

 

 

 

 

 

 

x c1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Интегрируя, получаем уравнение семейства окружностей

x c1 2 y c2 2 2

Значения произвольных постоянных и множителя Лагранжа определяются из граничных условий и условия связи.

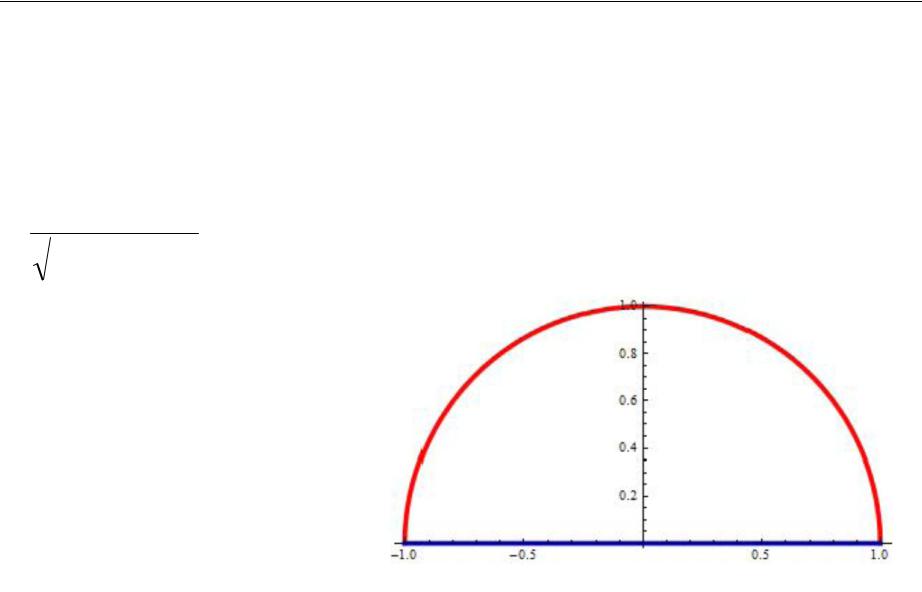
Пример 5.1 Решение вариационной задачи с изопериметрическим условием

Составим систему уравнений

 

 

 

 

 

 

 

 

 

 

 

 

1 c1

2 0 c2 2 2

 

 

1

c1

2

0 c2

2

2

 

 

 

 

1

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

x c1

2

 

1

 

 

 

 

 

инайдем произвольные постоянные

имножитель Лагранжа

c1 0

с2 0

1

Окончательно решение:

x2 y2 12

Лабораторная работа № 7

Задача вариационного исчисления с ограничениями. Изопериметрическая задача

1.Решить задание лабораторной работы 2a при заданном изопериметрическом условии.

2.Вычислить значение функционала на этой экстремали. Сравнить результат с решением лабораторной работы 2a.

3.Оформить отчет.

Соседние файлы в папке Вариационные методы Старинова
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности