Самарский государственный аэрокосмический университет
Лекция 2. Уравнение Эйлера
О. Л. Старинова
Кафедра Космического машиностроения |
2017 г. |
Сильный и слабый экстремум
Функционал J(y), y C1 a,b достигает при y y0 слабого экстремума, если 0 , такое что J(y)- J(y0) сохраняет знак при всех 
y y0 
C1 .
Функционал J(y), y C a,b достигает при y y0 сильного экстремума, если 0, такое что J(y)- J(y0) сохраняет знак при всех 
y y0 
C .
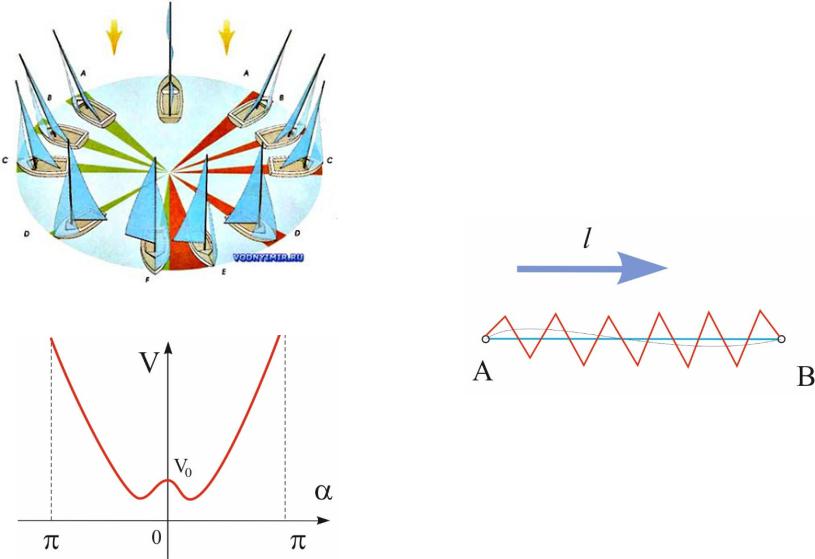
Сильный и слабый экстремум
Пусть яхте требуется пройти против ветра из точки А в точку В за min время.
Скорость яхты зависит от угла между направлением движения и ветром, как показано на рисунке.
Прямая AB доставляет слабый минимум времени движения. Однако пилообразные траектории движения доставляют сильный, глобальный min.
Необходимое условие экстремума
Th 2.1 Для того, чтобы функционал J(y) при y y |
0 |
|||||||||||
|
|
Курс |
||||||||||
достигал экстремума, необходимо, чтобы его вариация |
||||||||||||
|
вариационные методы |
|
|
|||||||||
|
J 0 |
(2.1) |
||||||||||
(если она существует) обращалась в ноль |
||||||||||||
|
Рассмотрим для определенности минимум. |
|
||||||||||
J J y0 x y |
J y0 x 0 |
(2.2) |
||||||||||
для всех достаточно малых y . |
|
|||||||||||
По определению вариации |
|
|||||||||||
J J y0 x , y y0 x , y |
|
|
|
y |
|
|
|
знаком J, |
(2.3) |
|||
|
|
|
|
|||||||||
Знак выражения (2.3) определяется |
|
|
|
|
|
|
|
|
||||
но |
J - линейный функционал, поэтому |
|
||||||||||
J |
y0 x , y J |
y0 x , y , и, следовательно, при |
||||||||||
J 0 выражение |
может быть, как положительным, так и |
|||||||||||
отрицательным, т.е. минимум в данном случае не достигается. Поэтому должно выполняться J 0
Первая вариация интегрального функционала
Рассмотрим интегральный функционал
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
(2.4) |
J y |
F x, y, y' dx extr |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
В этом случае вариация J(y) вызывается изменением |
||||||||||||||||
(вариацией) функции y(x) и её производной y’(x): |
||||||||||||||||
y |
x |
|
y |
x |
|
y |
x |
|
, |
y x |
|
y |
x |
|
y x |
|
|
|
0 |
|
|
|
|
|
0 |
|
|
||||||
(2.5)
Вычислим вариацию функционала как линейную часть его приращения. Для этого разложим F(x,y0+ y0,y 0+ y ) в ряд Тейлора в окрестности экстремальной функции y0 с удержанием только линейных членов, а затем проинтегрируем по частям:
Первая вариация интегрального функционала
J y0 |
x2 |
F x, y0 y, y'0 y' F x, y0 , y'0 dx |
||||||||||||||||||||
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
F |
|
|
|
F |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
y |
|
|
|
|
|||
|
F x, y0 , y'0 |
|
|
|
|
|
|
|
F x, y0 , y'0 dx |
|||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
y |
|
|
|
|
|
|
|||||
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x2 |
|
|
|
|
|
|
|
|
|
|
u F |
, du |
dFy |
dx |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
||||||||||
Fy y Fy' y' dx |
|
y |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x1 |
|
|
|
|
|
|
|
|
|
|
dv y'dx, v y |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
Fy ydx Fy ' y |
|
xx12 |
dFy ' |
ydx |
|
|
||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
x |
dx |
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Fy ' y |
|
x2 |
x2 |
|
|
|
|
dFy' |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Fy |
|
|
|
|
ydx |
|
|
|
|
(2.6) |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
x1 |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
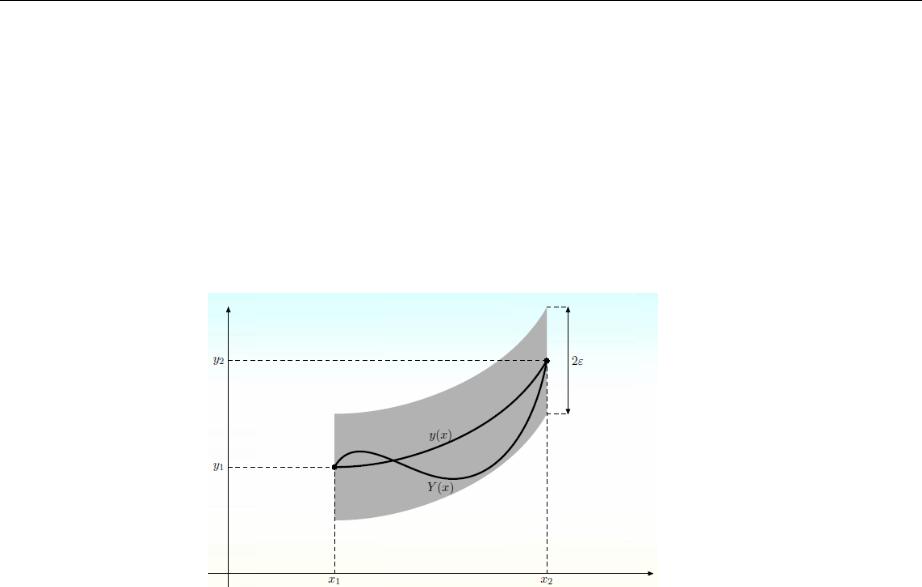
Простейшая задача вариационного исчисления
- задача с фиксированными граничными значениями
Если для функционала (2.4) заданы фиксированные граничные условия:
y x1 |
y1 |
, |
(2.7) |
|
y2 , |
||
y x2 |
|
||
то задача (2.4), (2.7) называется простейшей задачей вариационного исчисления.
Простейшая задача вариационного исчисления.
Дифференциальное уравнение Эйлера
Согласно необходимому условию экстремума, формуле для первой вариации функционала (2.4) и граничным условиям (2.7) , экстремум функционала достигается при выполнении следующих условий:
y x1 y x2 |
0 |
(2.8) |
|||
|
|
|
|
|
|
F |
dFy' |
0 |
|
|
(2.9) |
|
|
||||
y |
dx |
|
|
||
|
|
|
|
||
Это уравнение называется дифференциальным уравнением Эйлера.
Экстремалью называется интегральная кривая дифференциального уравнения Эйлера. Все экстремали в одной задаче образуют поле экстремалей.
Пример 2.1 Решение дифференциального уравнения Эйлера.
Найти экстремаль функционала
2 2 |
2 |
y 1 1; |
1 |
|
|
|
|
J y x y y' dx; |
|
1 |
y 1 2. |
Запишем уравнение Эйлера для этого функционала.
Fy F |
2 y, Fy F |
2 y , |
dFy' |
2 y |
|
||||
y |
y |
|
dx |
|
2 y 2 y 0 |
y'' y 0 |
|||
Это обыкновенное ДУ второго порядка. Соответствующее характеристическое уравнение и его корни:
k 2 1 0 |
k |
1 |
|
1,2 |
|
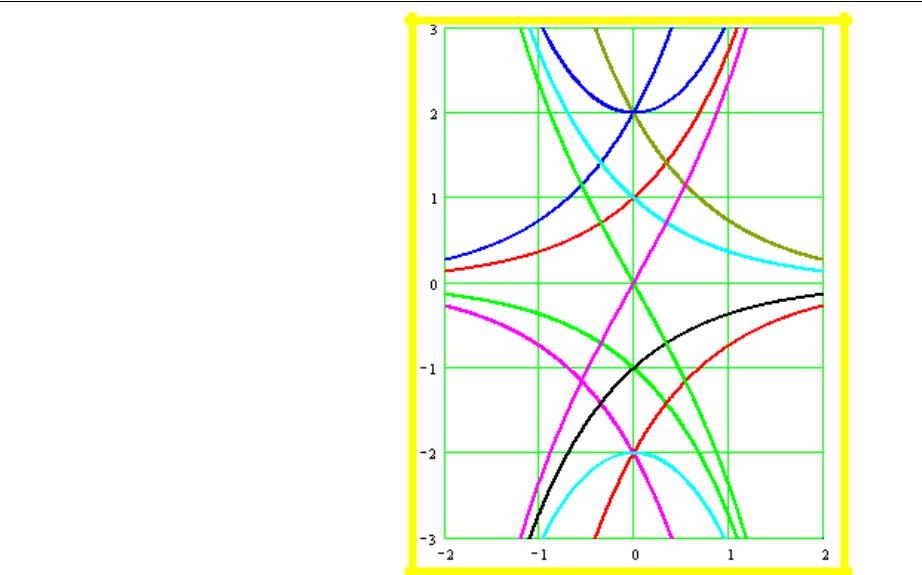
Пример 2.1 Решение дифференциального уравнения Эйлера. Продолжение.
Соответствующее общее решение
y x C1ex C2e x
определяет поле экстремалей, показанное на рисунке.