Самарский государственный аэрокосмический университет
ОСНОВЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
О. Л. Старинова
Кафедра Космического машиностроения |
2017 г. |
Структура курса
Курс вариационные методы
9 лекций |
8 лабораторных |
Самостоятельная |
|
работ |
работа 20 час |
Зачет
Рейтинг
Курс вариационные методы
Зачет ставится при условии: Количество набранных баллов ≥ 60
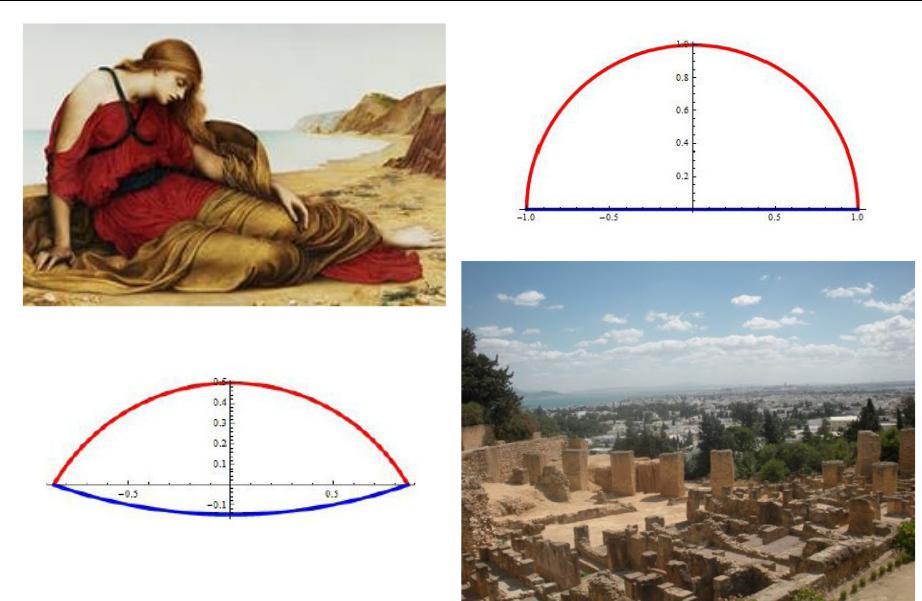
Задача Дидоны
Задача о брахистохроне
Была поставлена в 1696 году Иоганном Бернулли и решена 26 января 1697 года Исааком Ньютоном.
Задача о цепной линии
Перевёрнутая цепная линия — идеальная форма для арок. Однородная арка в форме перевёрнутой цепной линии испытывает только деформации сжатия.
Изопериметрические задачи
Мыльная плёнка, натянутая на два кольца, принимает форму катеноида — поверхности которая проходя через две окружности, имеет минимальную площадь. Такая поверхность излучает наименьшее количество тепла.
Основной принцип геометрической оптики
Пьер Ферма сформулировал основной принцип геометрической оптики, в силу которого свет в неоднородной среде выбирает путь, занимающий наименьшее время.
Принцип наименьшего действия
Основной принцип современной физики, химии, социологии, и многих других наук. Впервые был сформулирован Пьером Луи де Монпертюи для оптики и механики. В дальнейшем его идею развили Гамильтон, Эйлер и Лагранж.
Применение вариационного исчисления
•Задачи сопротивления материалов и прочности
•Задачи теоретической механики
•Задачи теории оптимального управления
Карл Густав |
Карл Тееодор Вильг еельм |
|
Якоб Якоби |
Софья Васильевна |
|
|
Веейерштрасс |
Ковалевская |