Самарский государственный аэрокосмический университет
Лекция 4. Функционалы, зависящие от
старших производных. Уравнение Эйлера-Пуассона. Вариационная производная
О. Л. Старинова
Кафедра Космического машиностроения |
2015 г. |
Функционалы, зависящие от старших производных.
Интегральный функционал может зависеть не только от неизвестной функции и ее первой производной, но и от производных высших порядков.
b |
(4.1) |
|
J ( y) F x, y, y , y , y ,... dx |
||
|
a
Получим условия оптимальности, аналогичные уравнению Эйлера, для функционала такого вида на основе необходимого условия
существования экстремума J=0. Для этого исследуем на экстремум функционал, зависящий от функции одной переменной и её производных 1-го и 2-го порядка
|
x2 |
|
|
|
J y |
F x, y, y', y'' dx extr |
(4.2) |
||
|
x1 |
|
|
|
c фиксированными граничными условиями: |
|
|||
y x1 |
y1 ; |
y' x1 |
y'1 ; |
(4.3) |
|
y2 ; |
|
y'2 . |
|
y x2 |
y' x2 |
|
||
Функционалы, зависящие от старших производных.
Вычислим J=0 как линейную часть приращения функционала. Разложим первое слагаемое в ряд Тейлора в окрестности экстремали, и удержим только линейные члены. Слагаемое, содержащее 1-ю производную, проинтегрируем по частям один раз, а слагаемое, содержащее 2-ю производную – 2 раза.
J y0 |
x2 |
F |
x, y0 y, y'0 y', y''0 y'' F |
x, y0 , y'0 , y''0 dx |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
Fy y Fy ' y' Fy'' y'' dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.4) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
Fy ydx Fy ' y |
|
x2 |
x2 |
dFy ' |
ydx Fy '' y' |
|
x2 |
x2 |
dFy'' |
y' dx |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x1 |
|
|
dx |
|
|
|
|
|
|
|
|
x1 |
|
dx |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
dF |
|
|
|
|
|
dF |
|
|
|
|
x2 |
x2 d 2 F |
|
|
|
|
|
x2 |
|
|
|
dF |
|
d 2 F |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
y' |
|
|
y '' |
|
|
|
|
|
|
|
y'' |
|
|
|
|
|
|
|
|
|
|
y' |
|
|
|
y'' |
||||||||
|
|
F |
|
|
|
|
|
ydx |
|
|
|
y |
|
|
|
|
|
|
|
ydx |
|
|
F |
|
|
|
|
|
|
ydx 0. |
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|||||||||||||||||||||||
|
y |
|
|
|
dx |
|
|
|
dx |
|
|
|
|
|
dx |
|
|
|
|
|
|
y |
|
dx |
|
|
dx |
|
|||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
x1 |
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
Функционалы, зависящие от старших производных.
При вычислении вариации функционала было учтено, что граничные условия на концах интервала фиксированы (4.2), поэтому y(x1)=0,
y(x2)=0, y’(x1)=0, y’(x2)=0.
В силу произвольности вариации функции y(x) по основной лемме вариационного исчисления первый сомножитель под интегралом должен равняться нулю:
Fy |
dF |
y' |
|
d 2 F |
y'' |
0 |
|
|
|
|
|
(4.5) |
|||
|
dx |
dx2 |
|||||
Подобное уравнение может быть легко получено и для функционала, зависящего от старших производных:
|
dF |
|
d 2 F |
|
d 3 F |
|
|
n d |
n |
|
F |
|
|
|
||||||
Fy |
y ' |
|
|
y'' |
|
|
y |
... 1 |
|
|
|
|
0 |
(4.6) |
||||||
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
||||||||
dx |
dx |
dx |
|
|
|
dx |
n |
y |
n |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Уравнение (4.6) называется уравнением Эйлера-Пуассона.
Пример 4.1 Решение вариационной задачи для функционала, зависящего от старших производных
Найти экстремаль функционала при заданных граничных условиях и построить график экстремали в виде двух функций y(x), y’(x).
1 |
y''2 2 y'2 4 yy' y2 2 y sin 2x dx; |
y 1 1; |
y 1 2; |
J y |
|
|
|
|
y' 1 1; |
y' 1 1. |
|
1 |
|
||
Уравнение Эйлера-Пуассона после сокращения на 2 примет вид |
|||
yIV 2 y'' y sin 2x |
yIV 2 y'' y 0 |
||
Соответствующие однородное уравнение |
|||
и характеристическое уравнение |
|
|
|
k 4 2k 2 1 0
Корни характеристического уравнения комплексно-сопряженные, кратные:
k 4 2k 2 1 k 2 1 2 0, k1,2 i, k3,4 i
Пример 4.1 Продолжение
Соответствующее общее решение однородного уравнения имеет вид:
y0 x c1x c2 cos x c3 x c4 sin x
Частное решение будет иметь вид
yч x Acos 2x B sin 2x
Найдем производные частного решения и неопределенные коэффициенты
yч x 2Asin 2x 2B cos 2x
y x 4Acos 2x 4B sin 2x
ч
y x 8Asin 2x 8B cos 2x
ч
yчIV x 16Acos 2x 16B sin 2x
16Acos 2x 16B sin 2x 8Acos 2x 8B sin 2xAcos 2x B sin 2x sin 2x
Пример 4.1 Продолжение
16A 8A A 0 |
|
A 0 |
|
|
16B 8B B 1 |
|
|
|
B 1/ 9 |
||
С учетом найденных произвольных постоянных окончательно имеем
решение
y x y0 x yч x
c1x c2 cos x c3 x c4 sin x 19 sin 2x
С помощью MathCad и с учетом граничных условий находим четыре постоянные и строим графики экстремали и ее производной.
Пример 4.1 Продолжение |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
y( x c1 c2 |
c3 c4) |
( c1 x |
c2) cos( x) |
( c3 x |
c4) sin( x) |
1 |
sin( 2 x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy( x |
c1 c2 c3 c4) |
d |
y( x |
c1 c2 c3 c4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
d x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy( x |
c1 c2 c3 c4) |
c1 cos( x) |
|
( c1 x |
c2) sin( x) |
|
c3 sin( x) |
( c3 x |
c4) cos( x) |
2 cos( 2 x) |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
given |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( c1 |
c2) cos( 1) |
( |
c3 |
|
c4) sin( |
1) |
|
1 sin( |
1) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( c1 |
c2) cos( 1) |
( c3 |
c4) |
sin( 1) |
1 |
sin( 2) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c1 cos( 1) |
( c1 |
c2) sin( |
1) |
|
c3 sin( |
1) |
( |
c3 |
|
c4) cos( |
1) |
2 cos( |
2) |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
c1 cos( 1) |
( c1 c2) sin( 1) |
c3 sin( 1) |
|
( c3 |
c4) cos( 1) |
2 cos( 2) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
( |
18 sin( 1) |
cos( 1) sin( 1) |
9 cos( 1) |
|
4 cos( 2) |
sin( 1) cos( 1) sin( 2) ) |
|
|
||||||
|
|
|
|
18 |
|
cos( 1)2 |
cos( 1) sin( 1) |
|
sin( 1)2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
27 sin( 1) |
cos( 1) sin( 1) |
27 cos( 1) |
|
cos( 1) sin( 2) |
sin( 1) sin( 2) |
sin( 1)2 |
|
1.799 |
||||||||||||
( Find( c1 c2 c3 c4) ) |
|
|
|
|
|
18 |
|
|
|
|
|
|
cos( 1) sin( 1) |
cos( 1)2 |
sin( 1)2 |
|
|
|
|
1.421 |
|||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
sin( 1) |
|
|
|
|
0.866 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( sin( 1) |
27 |
sin( 2) ) |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
cos( 1) sin( 1) |
|
cos( 1)2 |
sin( 1)2 |
|
|
0.677 |
||||
|
|
|
|
|
|
1 |
|
4 |
cos( 1) cos( 2) |
|
cos( 1) sin( 1) |
27 cos( 1) |
cos( 1) sin( 2) |
9 sin( 1) |
sin( 1)2 |
sin( 1) sin( 2) |
|
|
|||||||||||||
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
cos( 1)2 |
|
|
|
|
sin( 1)2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos( 1) sin( 1) |
|
|
|
|
|
||||||||||
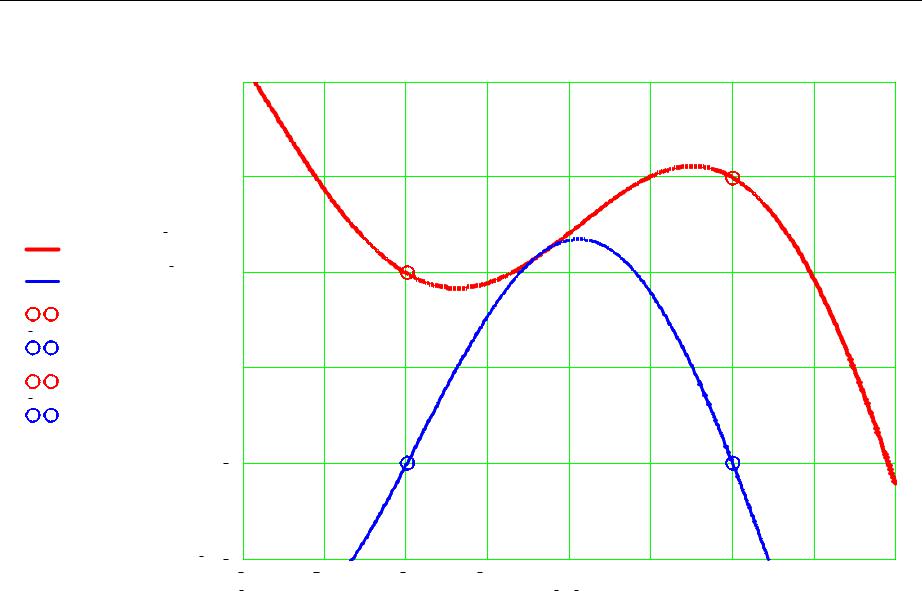
Пример 4.1 Продолжение |
|
|
|
|
|
|
||||||
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
y( x 1.799 |
1.421 |
0.866 |
0.677 ) |
|
|
|
|
|
|
|
|
|
dy( x 1.799 1.421 0.866 0.677 ) |
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1.5 |
1 |
0.5 |
0 |
0.5 |
1 |
1.5 |
2 |
|
|
|
|
2 |
|
|
|
x x 1 |
1 1 1 |
|
|
2 |
Лабораторная работа № 4
Экстремаль функционала, зависящего от производных старших порядков.
1.Для своего варианта функционала найти экстремаль и построить графики экстремали и ее производной.
2.Вычислить значение функционала на этой экстремали.
3.Оформить отчет.