ВВС-ЛабРабота-11-СОТР_КА

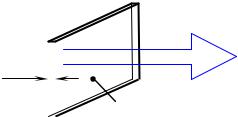
Курс "Введение с специальную технику"

ЛАБОРАТОРНАЯ РАБОТА №11

Расчет площади радиационного теплообменника КА

В данной лабораторной работе изучим принципы работы системы обеспечения теплового режима КА и рассчитаем проектные характеристики некоторых компонентов данной бортовой системы.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1) Способы теплообмена:

При описании процессов теплообмена часто используют термин - теплопередача, который означает физический процесс передачи тепловой энергии от более горячего тела к более холодному либо непосредственно (при контакте), либо через разделяющую (тела или среды) перегородку из какого-либо материала.

В настоящее время известны три вида теплопередачи:

1)теплопроводность (процесс переноса внутренней энергии от более нагретых частей тела (или тел) к менее нагретым частям (или телам), осуществляемый хаотически движущимися частицами тела (атомами, молекулами, электронами и т.п.));

2)конвекция (явление переноса теплоты в жидкостях или газах потоками вещества);

3)тепловое излучение (передача энергии от одних тел к другим в виде электромагнитных волн

за счёт их тепловой энергии).

Математические модели, описывающие процесс конвекции, являются более сложными относительно других и в рамках данной лабораторной работы рассматриваться не будут.

Для описания процесса теплопроводности используется выражение (1), которое иначе называется законом теплопроводности Фурье:

времени через единицу площади); - коэффициент теплопроводности [Вт/К·м], grad T - градиент изменения температуры в направлении передачи теплового потока [К].

Выражение (1) в зависимости от формы, проводящего тепло, тела может преобразовываться к множеству частных видов. К примеру, для описания процесса теплопередачи через плоскую пластину толщиной пл и площадью Sпл (см. рис. 1) можно использовать выражение (2):

Рисунок 1 - Тепловой поток через плоскую пластину

1

Курс "Введение с специальную технику"

Для описания процесса теплового излучения в первом приближении можно использовать выражение (3), которое иначе называется законом Стефана-Больцмана:

T - температура излучающей поверхности.

2) Уравнение теплового баланса:

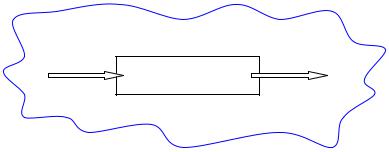
Рассмотрим рисунок 2, на котором во внешней среде выделен некоторый объект. Со стороны внешней среды объекту передается тепло в виде внешнего теплового потока мощностью Qвх . Объект сам передает во внешнюю среду тепло в виде теплового потока мощностью Qвых .

Внешняя среда

Рисунок 2 - К выводу уравнения теплового баланса

Уравнение теплового баланса для объекта в данном случае можно записать следующим образом:

количеству теплоты, которое необходимо передать телу массой 1 кг для того, чтобы его температура

времени.

К примеру, если внешняя среда вокруг объекта является идеальной пустотой, то есть в ней полностью отсутствуют внешние входящие тепловые потоки Qвх 0 Вт, а соответственно единственным возможным видом передачи тепла от объекта во внешнюю среду является тепловое излучение, то уравнение теплового баланса запишется следующим образом:

Курс "Введение с специальную технику"

3) Внешние тепловые потоки в околоземном космическом пространстве:

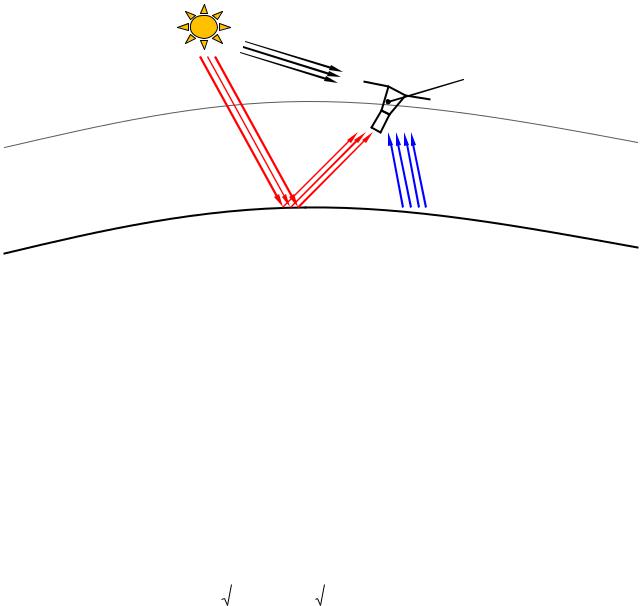
Двигаясь по рабочей орбите, КА находится в состоянии теплового обмена с окружающим околоземным космическим пространством. На КА действуют следующие основные внешние тепловые потоки (см. рис. 3):

тепловое излучение от Солнца ( Qсолн );

тепловое излучение солнечной энергии, отраженной от поверхности Земли ( Qотр );

собственное тепловое излучение Земли ( Qпл ).

Qсолн

КА

Земля

Рисунок 3 – Внешние тепловые потоки Мощность теплового излучения от Солнца можно определить из выражений (7):

что расстояние от центра Земли до КА намного меньше расстояния от Солнца до Земли, считаем, что

направлениями из центра Земли на Солнце и на КА.

Мощность теплового потока собственного излучения Земли можно определить из выражений (9):

3

Земли [Вт/м2].

4) Принцип работы и устройство системы обеспечения теплового режима КА:

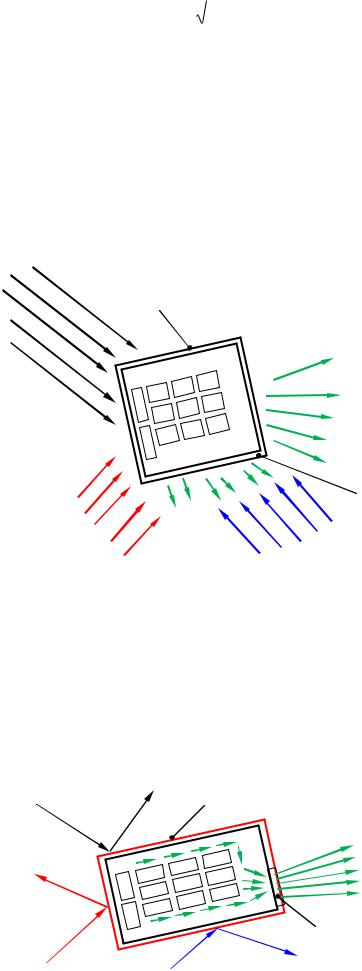
Если провести анализ, то наружная поверхность КА в околоземном пространстве, на освещенной стороне испытывает значительное тепловое воздействие от Солнца с удельной мощностью порядка qсолн 1400 Вт/м2. С другой стороны, КА сам излучает тепловую энергию в пространство и на теневых участках начинает охлаждаться. В результате этого, для незащищенной поверхности (к примеру, из стали) температура может колебаться от минус 150° С до плюс 150° С. Это схематически показано на рисунке 4.

Тпов = +150° С

Qсолн

QКА

Qотр

Тпов = - 150° С

Qпл

Рисунок 4 - Температурные условия на незащищенной поверхности КА

В тоже время, как правило, множество бортовых систем КА способно работать в диапазоне температур от 0° С до 40° С, а некоторые бортовые приборы и космонавты требуют соблюдения температурного режима 20° ± 2° С. Поэтому для возможности управления температурами бортовых систем КА система обеспечения теплового режима (СОТР) КА включает следующие компоненты:

термозащитное покрытие поверхности КА;

систему терморегулирования внутри КА.

На рисунке 5 схематично показано устройство системы обеспечения теплового режима КА.

Qсолн Термозащитное покрытие КА

QКА

Qотр

Радиатор охлаждения КА

Qпл

Рисунок 5 - Схема СОТР КА

4

Курс "Введение с специальную технику"

Для создания термозащитного покрытия КА выбирается материал с такими оптическими свойствами, при которых все внешние тепловые потоки отражаются почти полностью отражаются назад в космическое пространство (см. рис. 5). Свойство материала поглощать тепловое излучение описывается следующими коэффициентами:

AS - коэффициент поглощения солнечного излучения (показывает долю поглощения солнечной энергии поверхностью из рассматриваемого материала, 0 AS 1 );

W - коэффициент степени черноты тела (показывает долю поглощения остальной

тепловой энергии поверхностью из рассматриваемого материала, 0 W 1).

При этом суммарный тепловой поток поглощаемый поверхностью КА можно определить

поглощаемый поверхностью КА также будет стремиться к нулю ( Qвнешн 0 ).

Система терморегулирования внутри КА создается таким образом, чтобы собирать избыточное тепло от бортовых приборов и выбрасывать его в космическое пространство через специальный участок поверхности, который называется - радиационный теплообменник или радиатор охлаждения (см. рис. 5). Результатом работы системы терморегулирования является поддержание температуры бортовых систем в требуемом диапазоне, к примеру от 0° С до 40° С.

Так как тепло от внутренних бортовых систем КА выбрасывается в космическое пространство в виде теплового излучения, то для расчета мощности данного потока через радиационный теплообменник (РТО) используется закон Стефана-Больцмана:

термозащитного покрытия поверхности КА; WРТО - степень черноты поверхности радиационного

n

теплообменника; Ni t - суммарная мощность энергопотребления бортовых приборов КА в

i 1

текущий момент времени t .

Решая дифференциальное уравнение (12) можно рассчитать требуемы проектные характеристики элементов системы обеспечения теплового режима КА.

5

Курс "Введение с специальную технику"

5) Расчет требуемой площади радиационного теплообменника КА:

Рассмотрим пример расчета требуемой площади радиационного теплообменника КА. Пример 1: Имеется КА со следующими характеристикам: площадь поверхности КА

Sпов 10 м2; оптический коэффициент поглощения солнечного излучения поверхностью КА

AS 0,2 ; коэффициент степени черноты поверхности КА W 0,1. Внутри КА расположены три прибора с мощностями энергопотребления: N1 100 Вт, N2 80 Вт, N3 50 Вт соответственно.

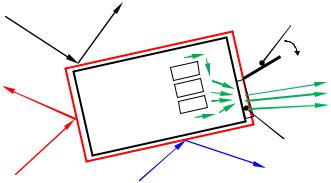
Для обеспечения теплового режима и выброса в космическое пространство излишнего тепла на КА установлен радиационный теплообменник с жалюзи, которые периодически закрывают его (см. рис. 6). Радиационный теплообменник имеет форму прямоугольного листа толщиной РТО 0,005 м и площадью SРТО . Радиационный теплообменник сделан из материала с

плотностью РТО 2300 кг/м3, удельной теплоемкостью cРТО 930 КДж/кг·К, степенью черноты внешней поверхности WРТО 0,3 и начальной температурой поверхности Tнач 20 ° С.

Считаем, что все приборы мгновенно передают свою мощность на радиационный теплообменник, а внешние тепловые потоки непрерывно действуют на всю поверхность КА.

Требуется подобрать такую площадь радиационного теплообменника SРТО , чтобы за период в 25 часов температура его поверхности отклонилась от начальной Tнач не более чем на 1 градус.

Qотр

Радиатор охлаждения КА

Qпл

Рисунок 6 - Схема КА

Решение:

1) Уравнение теплового баланса для радиационного теплообменника запишется следующим образом:

2) С другой стороны изменение температуры внешней поверхности можно определить из выражения:

где t - текущее время полета КА.

6

Курс "Введение с специальную технику"

3) Подставив выражение (13) в (12) получим следующую зависимость температуры поверхности радиатора от текущего времени полета:

Решая данное дифференциальное уравнение численным способом можно получить зависимость TРТО t на заданном временном интервале и провести оценку изменения температуры.

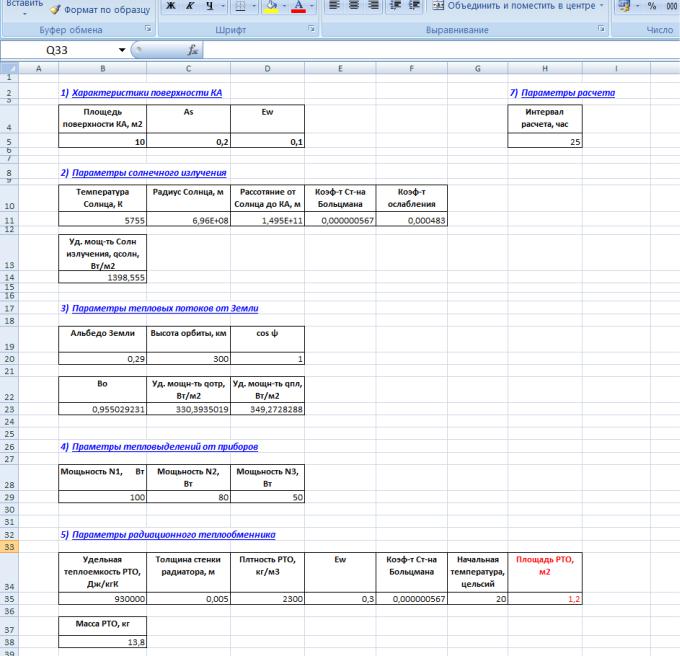
4) К примеру, если решать данную задачу с помощью MS Excel, то для начала следует сформировать исходные данные в следующей форме (см. рис. 7).

Рисунок 7 - Исходные данные для расчета

Обратите внимание, что площадь радиационного теплообменника SРТО присутствует в исходных данных, но выделена красным цветом. Это объясняется тем, что мы далее будем с клавиатуры изменять её, пока не подберем интересующую нас зависимость TРТО t .

5) Далее сформируем расчетную таблицу (см. рис. 8)

7

Курс "Введение с специальную технику"

Рисунок 8 - Расчетная таблица

5) Если теперь в ячейку площади РТО (выделено красным на рис. 7) ввести значение SРТО 3,0 м2, то получим график зависимости TРТО t как на рисунке 9.

Рисунок 9 - Зависимость TРТО t на интервале 25 часов

Из рисунка 9 видно, что за период в 25 часов температура внешней поверхности радиационного теплообменника изменилась не более чем на один градус, а следовательно площадь SРТО 3,0 м2 нас удовлетворяет.

8

Курс "Введение с специальную технику"

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Перечислите виды теплопередачи и объясните физическую сущность каждой.

2.Для описания какого процесса используется закон Фурье?

3.Для описания какого процесса используется закон Стефана-Больцмана?

4.Уравнение теплового баланса в общем виде.

5.Перечислите внешние тепловые потоки в околоземном пространстве и схематично покажите направление их действия.

6.Какие два основных компонента включает СОТР?

7.Что описывают оптические коэффициенты поверхности КА?

8.Для чего служит радиационный теплообменник?

ЗАДАНИЕ

1) Имеется КА со следующими характеристикам: площадь поверхности КА Sпов 7 м2; оптический коэффициент поглощения солнечного излучения поверхностью КА AS 0,22 ; коэффициент степени черноты поверхности КА W 0,05 . КА движется по круговой орбите высотой Hорб 340 км. Внутри КА расположены три прибора мощности энергопотребления которых описываются следующими выражениями:

Для обеспечения теплового режима и выброса в космическое пространство излишнего тепла на КА установлен радиационный теплообменник с жалюзи, которые периодически закрывают его (см. рис. 6). Радиационный теплообменник имеет форму прямоугольного листа толщиной РТО 0,003 м и площадью SРТО . Радиационный теплообменник сделан из материала с

плотностью РТО 2100 кг/м3, удельной теплоемкостью cРТО 930 КДж/кг·К, степенью черноты внешней поверхности WРТО 0,2 и начальной температурой поверхности Tнач 10 ° С.

Считаем, что все приборы мгновенно передают текущую мощность на радиационный теплообменник. Из внешних потоков на КА непрерывно действует поток от планеты Qпл . Тепловые потоки от Солнца ( Qсолн и Qотр ) во времени описываются следующими зависимостями:

период в 20 часов температура его поверхности отклонилась от начальной Tнач не более чем на 0,5 градусов.

9