
- •При любом допустимом значении c она является решением этого уравнения;
- •Собственные значения и собственные векторы матрицы
- •Лекция 13. Функциональные ряды
- •Определение. Функциональный ряд
- •Ряд Xan сходится.
- •Пример. Исследовать на абсолютную и равномерную
- •Ряд сходится для всех х.
- •Лекция 14. Степенные ряды (продолжение) Вычисление радиуса сходимости степенного ряда.
- •Разложение функций в ряд Тейлора (Маклорена)
- •Лекция 15. Ряд Маклорена для основных функций
- •Можно показать, что при х е (-1; 1) остаточный член Rn(X)
- •Основных элементарных функций
- •1) Приближенное вычисление значений функции.
- •2) Приближенное вычисление определенных интегралов.
- •Лекция 16. Ряды Фурье
- •1, Cosx, sinx, cos2x, sin2x,..., cosnx, sinnx (2)
- •Разложение в ряд Фурье четных и нечетных функций
- •1) Пусть функция f(X) определена на отрезке [-л; л]. Если функция

МИНОБРНАУКИ РОССИИ
федеральное государственное бюджетное образовательное учреждение
высшего образования
«Московский государственный технологический университет «СТАНКИН» (фгбоу ВО МГТУ «СТАНКИН»)
Факультет ИТС
Кафедра «Прикладная математика»
Иванова О. К., Виноградова Ю. А.
Лекции по дисциплине «Математика» 3 семестр
для студентов МГТУ «СТАНКИН», обучающихся по направлениям 12.03.01 «Приборостроение», 27.03.01 «Стандартизация и метрология», 27.03.02 «Управление качеством».
Москва 2016 г.
Лекция 1. Дифференциальные уравнения. Основные понятия.
ВС/ С/ с/
случае прямолинейного движения материальной точки массой m и с координатой х, если учесть, что ускорение
.. drX а = х = —z-
dt2
есть вторая производная координаты по времени t, и предположить, что суммарная сила F, действующая вдоль оси движения, зависит известным образом в общем случае от времени, координаты и скорости
V — X, хо, поскольку по 2-ому закону Ньютона F = та, получаем равенство
тх = F(t, х, х)
связывающее время, функцию x( t) и ее производные и представляющее собой, таким образом, дифференциальное уравнение. Чтобы найти закон движения x = x(t), необходимо решить это уравнение.
Основные определения
Определение. (Обыкновенным) дифференциальным уравнением называется равенство вида
F(x,y,y\ ...,/w)) = 05 (1)
связывающее между собой независимую переменную х, искомую
функцию у(х) и ее производные у\у", до производной
некоторого порядка n включительно.
Определение. Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком этого уравнения. Пример. Дифференциальное уравнение
У sin х + ху4 - (ym)2 = 0
Определение 3. Решением (частным решением)
дифференциального уравнения на интервале I называется всякая функция у = ф( х), при подстановке которой в это уравнение вместе с ее производными, уравнение обращается в тождество относительно х е I.
Если решение дифференциального уравнения задается неявно уравнением Ф(х, у) = 0, то это равенство называют интегралом (частным интегралом) дифференциального уравнения.
Решить (или, как иногда говорят, проинтегрировать)
дифференциальное уравнение - означает найти все его решения.
Определение 4. График всякого решения дифференциального уравнения (или кривая на плоскости xy, заданная его интегралом) называется интегральной кривой этого уравнения.
Пример. Показать, что кривая, заданная уравнением у = 3х ~ sin 2 х, является интегральной кривой дифференциального уравнения у" + 4у = 12х.
Дифференциальные уравнения первого порядка (общие понятия)
Общий вид дифференциального уравнения 1-го порядка:
F (х, у, у') = 0.
Выразим из этого уравнения У , если это возможно.
В результате придем к уравнению
У' = f(X У) , (2)
которое называется дифференциальным уравнением 1-го порядка, разрешенным относительно производной.
Определение. Начальным условием для уравнения (2) называется равенство вида
У(х0) = Уо (3)
(используется также запись у|*=*0 = Уо), где ^ Уо - заданные числа (начальные значения). Геометрически начальные значения определяют точку (хо,Уо) на плоскости xy. Выполнение начального условия (3) для функции У = У(х) означает, что ее график проходит через эту точку.
Определение. Задача отыскания решения уравнения (2), удовлетворяющего заданному начальному условию (3), называется задачей Коши для этого уравнения.
Геометрически задача Коши состоит в отыскании интегральной кривой уравнения (2), проходящей через заданную точку (хо, уо) .
Теорема (существования и единственности решения задачи Коши для уравнения у = f (x,у)). Если функция f(x,у) и ее частная производная
f
ду непрерывны в некоторой области D, то для любой точки (хо>Уо) е D задача Коши для дифференциального уравнения у' = f(x’у) с начальным условием у(хо) = уо имеет и притом единственное решение.
Геометрический смысл этой теоремы состоит в том, что при выполнении ее условий через каждую точку области D (речь идет о геометрическом образе области D на плоскости xy) проходит единственная интегральная кривая дифференциального уравнения. Из теоремы следует, что такое дифференциальное уравнение имеет бесконечно много различных решений.
Определение. Функция У = ф(x С), зависящая от параметра (произвольной постоянной) C, называется общим решением уравнения (2), если:
При любом допустимом значении c она является решением этого уравнения;
любое частное решение уравнения (2) представимо в виде y = ф( х, Со) при некотором значении Со этого параметра.
Уравнение Ф(x,y,С) = 0, определяющее общее решение
уравнения (2) неявно, называют общим интегралом дифференциального уравнения.
С геометрической точки зрения общее решение (общий интеграл) представляет собой семейство интегральных кривых, зависящее от одного параметра C и «заполняющее» область D.
Графический метод построения интегральных кривых
Пусть G — область определения функции f (х, у) в
дифференциальном уравнении у' = f (х у), точка р(x, у) е G и у = у(х) - интегральная кривая, проходящая через эту точку. Согласно геометрическому смыслу производной равенство у'= f(х, у) означает, что число f (P) = f( х, у) равно угловому коэффициенту k = tg а касательной к интегральной кривой в точке P (а - угол наклона касательной). Таким образом, функция f(ху) определяет в каждой
G
направление касательной к проходящей через эту точку интегральной кривой. Небольшой отрезок прямой, проходящий через точку P с углом наклона а, определяемым равенством tg а = f (р)
, называют линейным элементом. Совокупность всех линейных элементов во множестве G образует поле направлений.

Множество всех точек плоскости, в которых направление поля, определяемого уравнением у'= f (х у), одно и то же, т.е. у’ = k = const, называется изоклиной. Всякая изоклина задается уравнением f (х, у) = k, где k — число, и обычно является некоторой кривой. Построив несколько изоклин для различных значений k и линейные элементы в точках каждой изоклины, направление которых определяется равенством tg « =k, получим поле направлений. Этот способ построения поля направлений, а затем и интегральных кривых, носит название «метод изоклин».
Пример. Для уравнения у' — У +2 — хт найти изоклину,
проходящую через точку (—, и выяснить направление поля в ее точках.
Уравнение семейства изоклин имеет вид
у+1—х2 — к, где к — любое число.
Положив х — — 1, у — 0, найдем к — 1, и, следовательно, уравнение искомой изоклины у+2—х2 — 1, т.е. изоклиной является парабола у — х2 — 1 . Поскольку к — 1, то линейные элементы в каждой точке найденной изоклины образуют угол а — arctg1 — у4 — 45° с осью х. ►
Пример. Методом изоклин построить поле направлений для
г\ г\
уравнения у— х + у . Построить приблизительно интегральную кривую, проходящую через начало координат.
Уравнение семейства изоклин имеет вид
х2 + у2 — к (к > 0),
т.е. изоклины (при к>0) — окружности радиуса с центром в начале
координат. Зададим для параметра к значения 0, у4, 1, 4.
Соответствующие изоклины — начало координат и окружности радиусами уг, 1 и 2 соответственно. В начале координат tgа = 0, т.е. линейный элемент направлен по оси х. В точках окружности радиуса
Yl из уравнения tg а = У4 находим а = arctg}4 ~ 14°; соответственно, для остальных двух окружностей а = ai-rtg1 = 45 ° и а = arctg4 « 76° . Построив в точках изоклин линейные элементы, получаем поле направлений. Интегральную кривую, проходящую через начало координат, проводим таким образом, чтобы она касалась оси х и, пересекая каждую из построенных окружностей, имела в точках пересечения соответствующий угол а наклона касательной (рис. 4). ►

Лекция 2. Решение некоторых типов дифференциальных
уравнений 1-го порядка.
Уравнения с разделяющимися переменными
Общий вид: Дифференциальное уравнение вида
У
(1)
' = f ( X) g(у)(т.е. если функцию f (х, У) в уравнении у = f (у) можно разложить в
1 U U W \
произведение функции, зависящих только от одной переменной), называется уравнением с разделяющимися переменными.
М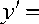
dy dx,
(2)
то путем деления обеих частей равенства dx f(x)g(y') g( У) * 0 ) и умножения на dx уравнение (1) приводится к виду
на
g(У)
(при
етод решения: Так какdy g (У)
(
f(x)dx
этот переход называется разделением переменных). Интегрируя обе части этого равенства (левую часть по у, а правую по х)J gy) = Jf (x)dX ,
получаем общий интеграл данного уравнения в виде
G( y) = F (x) + C,
откуда, если это возможно, выражаем общее решение.
Замечание: если какое-либо число у0 - нуль функции g(y), т.е. g(уо) = 0, то, очевидно, функция y = уо также является решением уравнения (1).
Пример. Решить уравнение
(2У2 + 1)y = 2xy .
◄ Данное уравнение приводится к уравнению с разделяющимися переменными
(f(х) = 2 x, g (*) = v+T).
, dy dy 2 xy
У —1 = 9
Полагая ■' dx , получим: dx 2y +1 разделяем переменные:
(
— 2 xdx
2 y2 + 1)dy
У
и интегрируем
I(2 y + —) dy — 12 xdx
y
общий интеграл уравнения;
2 + ln| y — x2 + Cк
.2
y2 + ln | y |— xz + C
?
роме того, при разделении переменных потеряно решение У — 0 , которое не может быть получено из общего интеграла ни при каком значении C. Таким образом, все решения данного уравнения задаются неявно общим интегралом(выразить отсюда общее решение в явном виде невозможно) и уравнением y 0 .
Ответ: y + ln 1 y = x + C; y 0 ►
Пример. Решить задачу Коши:
(y +1)2 dx + xdy = 0, У (e) = 0.
◄ Найдем сначала общее решение. Разделяем переменные:
dy _dx
( у +1)2 x
(теряемые решения y = —1 и x = 0 начальному условию не удовлетворяют). В результате интегрирования получим
1
7 = ln | x | + C у = — ■
У +1 , откуда ^ ln | x | +C
-1
. , , ~ 1Находим C из начального условия:
1
0 =
1 + C
--L-i
у
Ответ:
ln x (х > 1 )•Однородные дифференциальные уравнения 1-го порядка Определение: Функция M (x, у )
называется однородной степени а (или
измерения а), если
М(Хх, Ху) = XaM( х, у)
тождественно относительно x, у и Х ^ 0. Степень а может быть любым действительным числом. В частности, если
f (Xx, Ху ) = f ( х у ),
то f ( x, у) - однородная функция нулевой степени.
Пример. 1) функция М( х,у) = 3ху + У является однородной 2-й степени,
т.к. М(Хх, Ху) = 3(Хх)(Ху) + (Ху)2 = Х2 (3ху + у2) = Х2М( х, у),
x . y = -- sin—
X
2) функция f (X У) y 2
- однородная функция нулевой степени,т.к.
Г\ г\
(Xx)2 . Xy x . y
- - Sin^~ = ^т- Sin —
(Xy)2 XX y2 x .
Общий вид: Уравнение y ~ f (x?y) называется однородным
дифференциальным уравнением 1-го порядка, если f (x,y) есть однородная функция нулевой степени.
Это определение эквивалентно следующему определению:
о
(4)
Метод решения: Для решения однородного дифференциального уравнения
и ( x)
введем новую неизвестную функцию
положив
днородным дифференциальным уравнением 1-го порядка называется уравнение видат
?
 .е.
y
и
* x
.
Тогда при подстановке в уравнение (4)
.е.
y
и
* x
.
Тогда при подстановке в уравнение (4)
У = ux У У — urx + и
о
и X + и = g (и)
du
или dx
x = g (и) - и
?
но принимает видт
I
du
g ( и) - и
—I
dx
x
G (и) = ln | x | + ln Q
.е. преобразуется в уравнение с разделяющимися переменными. Решая это уравнение, получаем (произвольная постоянная для удобства потенцирования представлена в логарифмической форме)
и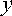 лиС(и)
=
ln
Cx
(
C
=
±Cl
),
лиС(и)
=
ln
Cx
(
C
=
±Cl
),
откуда, подставляя x вместо и, получим общий интеграл уравнения (4) вида
G
Замечание: если

корень уравнения g (и) - и = 0 , то и = Uo
решение
(y) = ln Cx (C * 0)преобразованного уравнения, а y = U0x - решение исходного уравнения.
Замечание: Если уравнение y = f(x,y) - однородное, то для решения не обязательно приводить его к виду (4) - после подстановки y UX переменная x из правой части уравнения исчезает в результате сокращения и f (x,y)
преобразуется в g(u).
Пример. Решить уравнение
(x + y )dy — ydx = 0
◄ Данное уравнение однородное, т.к. функции M(x?y) = — y и N(x, y) = x + у - однородные 1-го порядка (или по другому - приведя уравнение к виду, разрешенному
dy _ y
п
относительно
роизводной dx x + y , обнаруживаем, что функцияП
_ У
f (x, y) =
X + y
f
(x,
У)
= 'x
- однородная нулевой степени; либо, наконец,
=* (У)
и
1 + У/ °'х'> где *(и) 1 + и )•
X
У =
У
иХ + и =
их
х + у , получим "" ' х + их , или, после преобразований, уравнение с
разделяющимися переменными
du и
— х = -
dx2
1 + и •
Разделяем переменные
(1 + и)d^ _ dx
и
х
и интегрируем:
1
— ln | и = ln | х + ln C1 и
Отсюда
оложим У их . Тогда У = их + и . Подставив эти выражения в уравнение
— =
ln C | ux u™и u
— = ln
Cux ^C = ±C).
u = У
Возвращаясь к функции у ( x ), получим общий интеграл:
x = y ln Cy
К
u = 0
, а,
роме этого, при разделении переменных теряется решение следовательно, исходное уравнение имеет решение y = 0.Ответ: Х = Уln СУ (C * 0); У = 0 . ►
Л
y' + a ( x ) y = b( x )
(т.е. содержит у и y в первой степени), где a(x) и b(x)
на интервале I.
(5)
- функции, непрерывные
инейные дифференциальные уравнения 1-го порядка Общий вид: Линейным дифференциальным уравнением 1-го порядка называется уравнение видаМетод решения.
1
dx =I d
a (x )dx ^ ln | y
A( x) + ln C1
откуда общее решение
У — Ce~A( x)
(6)
) При b(x) = 0 уравнение (5) принимает вид y +a(x)y — 0, называется однородным линейным, является уравнением с разделяющимися переменными и легко решается:где A( x ) — одна из первообразных функции a ( x) (C — ± Ci).
2) Неоднородное линейное уравнение (5) обычно решают методом подстановки, а именно, будем искать его решение в виде произведения
У — u(x) • v(x)
Подставив y uv , y UV ^ UV в уравнение (5) получим
u
или
'v + uv' + a (x )uv — b( x)Выберем функцию K V‘/v / так, чтобы выражение в скобке обратилось в нуль, т.е. выберем какое-нибудь (ненулевое) частное решение однородного линейного
V
u'v + u( v' + a (x )v) = b( x) v (x)
+ a ( x )v = 0 v = e ~A( x)уравнения v / ; в качестве такового можно взять у ^ .
Подставляя эту функцию вместо v в уравнение (7), получаем уравнение с разделяющимися переменными относительно функции и:
u'v (x) = b( x)
Н
и = u( x) + C
аходим общее решение этого уравнения ~~ ■ — , после чего, перемножаянайденные функции v(x) и и(x) ^ C , получаем общее решение исходного уравнения (5):
у = v ( x )(и( x ) + C)
Пример. Решить уравнение
ху' = cos х — у
◄
Полагая здесь
У =
, у cosх
у +— =
х х
uv у у = u V + uv v
, получим
х или
х
(8)
1
х
v (х) , . v' + v = 0
v ' (* о), решая уравнение х
^ ln | v |= — ln | х | (C = 0) ^ v
, , uv cos х
u v + uv + =
х
Найдем какую-нибудь функцию
dv _ v dv _ dх
dK х v х
. . . v\ cos х
u v + u\v +— =
х
Подставляя

в уравнение (8), получим:
Данное уравнение приводится к линейному:u cos x du
— = — = cos x
x x или dx
Общее решение этого уравнения:
u = sin x + C
Так как У uv , то перемножая теперь найденные и и v, получаем общее решение исходного уравнения:
s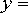 in
x
+
C
x
. ►
in
x
+
C
x
. ►
П
.2
ример. Решить задачу Коши: (x y ^ e )dx x dy 0, y 0◄
x = 0
x2y + ex - x2 dy = 0
dx
e
x
У - У = —
x2
(Решение x = 0, теряемое при разрешении исходного уравнения относительно у', начальному условию не удовлетворяет).
у = uv у' = u'v + uv'
Выполнив подстановку
, получим
Уравнение приводится к линейному:u
X
'v + u (v' - v) =
Из
v v 0 следует
dv dv r , ,
= v ^ — = dx ^ ln| v = x ^ v — e
X
dx
v
Д
.x
ufex —
,1 r \
u =^T ^ u — C
X'
X'
X
алееу
и общее решение
e (C ^X) . Из начального условия 0 = e(C 1),_ у = eX (X -1)
откуда C — 1 и X (X ^ 0) — искомое частное решение. ►
Замечание: Аналогично линейному уравнению решается уравнение Бернулли:

, где , а ф 1
(при а = 0 это уравнение является линейным, а при а = 1 - уравнением с разделяющимися переменными). Уравнение Бернулли можно также свести к
линейному с помощью подстановки уравнения Бернулли есть решение x = 0
Пример. ХУ — y = y . Замена
Z = у 1-а
У . Отметим, что при а ^ 0
у
1-2
Z = у =
у . Тогда
1 ,
у = -;у =
z
Основные понятия
Общий вид дифференциального уравнения n-го порядка
F(x,у,У, ...,Уи)) = О,
Общий вид дифференциального уравнения n-го порядка, разрешенного относительно старшей производной:
О
(1)
уравнения
(2)
для
пределение. Начальными условиямиу{п} = f{x,у,у', ...,у{п~Х))
называются n равенств вида
Х*о) = Лъ/(*о) = Уо, • • • ,У{п~1\хо) = Уо~1)
, где *0 , Уо> Уо> • • • 9 У о - заданные числа (начальные значения).
Замечание: число начальных условий совпадает с порядком дифференциального уравнения.
Определение. Задача отыскания решений уравнения
у(п) = fix,у,у',...,у{п~Х)) , удовлетворяющих заданным начальным условиям, называется задачей Коши для этого уравнения.
Теорема 1 (существования и единственности решения задачи Коши для уравнения ^ — У^Х->У->У ? •••?У^ ). Если функция /(Х>У>У> •••>У^п и ее
д± df_ df
ч
D с R
п+1
, то для любой точки (хо,Уо,Уо, --^Уо* 1}) задача Коши для
астные производные ду , ду', ду^п~^ непрерывны в некоторой областидифференциального уравнения У^ ^ ~ /Xх? У-> У ? • • • ? У^ с заданными
начальными условиями (2) имеет и притом единственное решение.
В частности, при п — 2 уравнение (1) имеет вид
У* — f (Х У? У) ,
а начальные условия -
У(Хо) — Уо , У'(Хо) — у0 .
Равенство У(Хо) = Уо геометрически означает, что кривая У — У(Х)
проходит через точку (Хо> Уо),
Равенство y (Хо) — у0 геометрически означает, что касательная к кривой в точке (Хо> У(Хо)) имеет угол наклона а, определяемый равенством
tg a = y0,
т.е. определяет направление кривой в этой точке.
Геометрический смысл Коши для уравнения y = f (x, У, У ) с начальными условиями У(xo) = У о, У'(xo) = Уо состоит в отыскании интегральных кривых
этого уравнения, проходящих через точку (х0? У0) в направлении, определяемом равенством tg a = уО .
Геометрический смысл теоремы существования и единственности решения задачи Коши для уравнения при n — 2
состоит в том, что при выполнении ее условий через точку (*0’ y0) на плоскости xy в заданном направлении проходит единственная интегральная кривая дифференциального уравнения. Таким образом, в отличие от уравнения 1-го порядка
через точку (*0, Уо) проходит бесконечно много интегральных кривых (в различных направлениях).
Определение. Функция У ~ ... ,CW) ? зависящая от п параметров
СъС2, • • • ?Сп 5 называется общим решением уравнения
У(п) = fix, у, У, ... ,У(П~1}) , если:
при любых допустимых значениях Q? С2, 0на является решением этого уравнения;
любое частное решение уравнения ^ У-> У ? • • • ?
представимо в виде У = Ф(х^ьС2, ... ,Сп) ПрИ некоторых значениях параметров
гг г
j • • • j ^п .
Уравнение Ф(х,у,Сь ...,С„) = Ог
неявно определяющее общее решение
уравнения У^ = /Xх? У? У ? • • • ? У^п ^) , называют общим интегралом этого уравнения.
Замечание: число параметров (произвольных постоянных) в общем решении (общем интеграле) совпадает с порядком дифференциального уравнения.
Пример. Показать, что функция У = Cie + C2e * является общим решением
уравнения y — y = 0. Найти частное решение этого уравнения, удовлетворяющее
начальным условиям у (0) = 0, У '(0) = 1.
◄ Проверим выполнение условий из определения общего решения.
Число произвольных постоянных в данной функции равно 2, что совпадает с порядком уравнения.
При любых значениях c и C2 эта функция является решением уравнения:
у = C1ex + C2e~x ^ У = C1ex - C2e~x ^ y" = C1ex + C2e~x;
подставляя / и y в уравнение, получим тождество:
Clex+C2e~x-(Clex+C2e~x) = 0 =^> 0 = 0 VxeM.
Каковы бы ни были начальные значения x0, у0, у0 (для данного уравнения область D существования и единственности решения совпадает с к3), система уравнений
<
V
У0 = Cxe*0 + C2e —x0, y0 = Qex° — C2e~X0
и
>х0
-Х0
Д =
= —2 ф 0
ex0 —e x0
т.е. для любых начальных условий значения параметров С1
меет (притом единственное) решение относительно c и C2, т.к. ее определительи ^2 , обеспечивающие их выполнение, существуют.
Поскольку все условия, входящие в определение общего решения выполнены, то данная функция действительно является общим решением данного уравнения.
Для нахождения частного решения после подстановки начальных значений
X = 0, у = 0 и у = 1 в общее решение и его производную получим систему
Г0 = Cl + C2,
1
2,
откуда С1 /2,
у = /2( ex — e-x ). ►

и, следовательно, искомое частное решение
= C — CУравнения, допускающие понижение порядка
В некоторых случаях удается свести дифференциальное уравнение n-го порядка к уравнению более низкого порядка.
а) Уравнение вида
у( п ) = /(х).
Метод решения: Общее решение этого уравнения получается путем n-кратного интегрирования (при каждом интегрировании порядок уравнения понижается на 1).
Пример. Решить уравнение
у” = х + 8 cos 4 х.
б) Уравнение 2-го порядка вида
F (х, уу') = 0
(не содержащее явно искомую функцию у).
Метод решения: Положим У = z(х) ; тогда у = z и уравнение сводится к уравнению 1-го порядка: F(х, z, z ) = 0. Если последнее уравнение решается аналитически и z z(х, С1) - его общее решение, то, интегрируя равенство
у' = z (х, Cj)
,
, где
получаем общее решение данного уравнения вида у = Z (х, Ci) + C2 Z ( х, Cj ) - одна из первообразных функции Z ( X, С1) .Пример. Решить уравнение
ху• + 2у' = 6х.
в) Уравнение 2-го порядка вида
F (у, у', у •) = 0
(не содержащее явно независимую переменную х).
М
У,
= p
<у dx <у . Подставляя в данное
етод решения: Положим у Р , причем p будем считать функцией от , *_<%'_ dp(у)_ dpd^_dp.
dx
уравнение выражения для функции Р ( у ) :
у • и у ••
получим уравнение 1-го порядка относительно
е. у ~ p(у). Тогда у <хF (у,р, р<у )=0.
Если Р = Р( у, С\) - общее решение последнего уравнения, то, решая уравнение с разделяющимися переменными у = p (у, Cl), получаем общий
d — D( y c )
интеграл данного уравнения: dx P( У,
P( У , Cl) — x + C2
Замечание: если P(у0, C1) — 0 , то y — y0также является решением уравнения
F(у, У, у") — 0 .
Пример. Решить уравнение
?
уу" + у “ — 0
2Пример. Найти частное решение уравнения
(у +1) У-У2 — О
у
удовлетворяющее начальным условиям
(0) — 1; у'(0) — 2? ?? 2
П
удовлетворяющее
ример. Найти частное решение уравнения уу — у начальным условиям у (0) — у '(0) — -1.Лекция 4. Линейные дифференциальные уравнения n-го порядка
Определение. Линейным дифференциальным уравнением n-го порядка называется уравнение вида
у(п) + ах{х)у(п~Х) + ... + а„_\(х)у' + ап(х)у = Ь(х) ^ (3)
где коэффициенты щ{х),а2(х), ••• >ап(х), а также правая часть Ь(х) ? предполагаются далее непрерывными функциями на некотором интервале I
(коэффициент при полагается равным 1, т.к. в противном случае все члены
уравнения можно на него поделить на интервале, где он отличен от нуля).
Пример. Уравнение
2 _
у'"- х2 у' sin х - xy
приводится к линейному дифференциальному уравнению 3-го порядка
ут - х2yf + 2xe~ху = 2e~х sin х. ►
При изучении линейных уравнений весьма удобно использовать понятие
линейного дифференциального оператора.
Цу) - У(п) + а\(х)У{п 1} + • • • + e„-i(*)/ + а„(х)у
Докажем, что оператор L обладает свойствами линейности:
а) L(У1 + У2) = L(УО + L(У2) для любых yi и y2 из множества всех функций, определенных на интервале I и имеющих на этом интервале непрерывные производные до порядка п включительно;
б) Щу) = Щ у) для любого У из указанного множества и любого ^ ^ Ж. Доказательство: а) Действительно, ввиду линейности операции дифференцирования
Ol + у2)(к) = У1(к) +У2(к) и (Уу)(к} =Уу(к) при к = \,2,...п.
Поэтому
^ЛУ\+У2) = {У\+У2^п) +а\{х\У\+У2^п + ... +ап(х)(у\ + у2) =
= Ух(п) +у2{п) +а1(х)Ып-"+у2^)+ ... + ап(х)(ух +у2) =
=
(у{п)
+ах{х)у!п~Х)
+ ... + ап(х)ух)
+ (у2{п)
+ ах(х)у2{п~Х)
+ ... +ап(х)у2)
=
=
L(
у1)
+ L(
у2)
6) L(\y) = (Ау){п) + ах{х)(\у){п 1} + ... + ап{х)\у =
= Ху№ + ai(x)Xy(n~^ + ... + ап{х)Ху = Х{у^ + аг(х)у(п~1^ + ... + ап(х)у) =
= Щj) в
Оператор, удовлетворяющий условиям а) и б), называется линейным. Таким образом, оператор L является линейным дифференциальным оператором.
Используя обозначение линейного дифференциального оператора, уравнение
у(п) +ах (х)у(п~Х) + ... + an_i (х)у' + ап (х)у = Ь(х)
можно теперь записать короче в виде
L( у) = Ь( х).
Однородные линейные дифференциальные уравнения
Если b( х) = 0 на I, то уравнение (3) имеет вид
у{п) + а1(х)-у(я~1) + ... + ап-х(х)у' + ап(х)у = 0 (5)
(или короче L( У) =
и называется однородным; в противном случае это уравнение называется неоднородным.
Свойства множества решений однородного линейного дифференциального уравнения (о.л.д.у.):
если yi(x) и У2(x) - какие-нибудь два решения о.л.д.у., то их сумма yi + y2 также есть решение этого уравнения;
Доказательство: Действительно, если У1( x ) и У2(x) - какие-нибудь два решения уравнения (5), то L( yi) = 0 и L( У 2) = о на I; поэтому, ввиду линейности оператора L
L(y1 + y2) = L(y1) + L(y2) = 0 + 0 = 0 ,
т.е. y1 ^ y2 - решение уравнения (5).
если y(x) - какое-нибудь решение о.л.д.у. и C - любое число, то их произведение Cy также есть решение этого уравнения.
Доказательство: Если y (x ) - какое-нибудь решение уравнения (5), то
L(Cy) = CL(у) = C •0 = 0, т.е. Cy - решение уравнения (5).
Следствие 1. Если УъУг^-^Ут - решения о.л.д.у. и Ci,C2,...,Cm - произвольные числа, то функция С\У\ + С2у2 +... + Стут также является решением этого уравнения.
Линейная зависимость системы функций.
Пусть дана совокупность (система) т функций 3^2(^0?***?Ут со,
определенных на некотором промежутке I.
Е
• ? ™ т - произвольные числа, то функция
m
а1 У\ + а2У2 + • • • + 01тУт ~ X] акУк
к=1
сли ^1 ? ^2 ? • •называется линейной комбинацией функций УъУт, а числа щ,а2,...,ат ко эффициентами этой линейной комбинации.
Определение. Система функций Уъ У2 ? • • • ? Ут называется линейно зависимой
на промежутке /, если существуют числа аъ а2? • • • ? ат, не все равные нулю и такие, что
Ы\У\ + ОС2 J2 + • • • + атУт = 0 Vx Е / •
если же это равенство возможно только при ocj = а2 =... = = 0 ? хо система
называется линейно независимой.
Необходимое и достаточное условие линейной зависимости системы
функций.
Для линейной зависимости системы, содержащей более одной функции, необходимо и достаточно, чтобы хотя бы одна из этих функций являлась линейной комбинацией остальных.
Две функции y 1 и У2 ( У2 * 0 ), в частности, тогда и только тогда линейно
У
— = const зависимы, когда у2 .
Пример. а) Система функций у1 = 1, y2 = х , yз = 2х -5 линейно зависима на любом промежутке, поскольку, например, при а1 = 5 , а2 = —2, аз = 1 имеем
Предположим теперь, что функции ••• >ут(х) дифференцируемы
(т — 1) раз
Определение. Вронскианом (определителем Вроньского) системы функций УъУъ--->Ут называется функциональный определитель, составленный из этих функций и их производных до (m ~ 1) -го порядка включительно, вида:
У\ У 2 ••• Ут
У
W ( X )
\ У2 • • • Уту'”-'1 у?-"... у<--"
Теорема 1 (необходимое условие линейной зависимости системы функций).
Если система УъУъ--->Ут (т-1) раз дифференцируемых функций линейно зависима на интервале I, то ее вронскиан тождественно равен нулю на этом интервале.
Доказательство: Если система УъУЪ”">Ут линейно зависима на интервале /, то
а1 У\ + а2У2 + • • • + остУт = О на /, где среди чисел аь а2 ? • • • ? есть неравные нулю.
Продифференцировав это тождество (m _ 1) раз, получим систему
а1 У\ + а2 У2 + • • • + ЫтУт = О?
Щ
<

,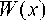 согласно условию существования ненулевого
решения у однородной системы m
х
m
равен
нулю. ■
согласно условию существования ненулевого
решения у однородной системы m
х
m
равен
нулю. ■
Следствие 1 (достаточное условие линейной независимости системы функций).
Если хотя бы в одной точке интервала Iвронскиан системы Уъ Уъ- • • ? Ут отличен от нуля, то эта система линейно независима на I.
Замечание: Тождественное равенство вронскиана нулю является лишь
необходимым условием линейной зависимости, т.е. из W(x) = 0 на интервале I, вообще говоря, не следует, что система линейно зависима на этом интервале.
Замечание: если система функций не произвольна, а состоит из решений однородного линейного дифференциального уравнения, то, как показывает следующая теорема, обращение вронскиана в нуль даже хотя бы в одной точке необходимо и достаточно для ее линейной зависимости.
Теорема 2 (необходимые и достаточные условия линейной зависимости решений однородного линейного дифференциального уравнения). Пусть функции
У
на интервале I, и

их вронскиан. Тогда следующие утверждения
ъУь — ,Уп являются решениями некоторого однородного линейного дифференциального уравнения n-го порядка, коэффициенты которого непрерывныэквивалентны:
функции УъУъ-->Уп линейно зависимы на интервале /;
W(х) равен нулю тождественно на I;
W(х) равен нулю хотя бы в одной точке х0 е 1.
Следствие 2 (необходимое и достаточное условие линейной независимости решений однородного линейного дифференциального уравнения). Для того чтобы n решений однородного линейного дифференциального уравнения n-го порядка были линейно независимы на интервале I непрерывности коэффициентов этого уравнения необходимо и достаточно, чтобы их вронскиан не обращался в нуль на этом интервале.
Вывод: Таким образом, для вронскиана n решений однородного линейного дифференциального уравнения n-го порядка возможны лишь две альтернативы - либо он тождественно равен нулю на интервале I (и в этом случае решения линейно зависимы), либо он не обращается в нуль ни в одной точке этого интервала (и в этом случае решения линейно независимы).
И
у(п) + ах (.х)у(п 1} + ... + ап_х (х)/ + ап (x)j = О
(1)
сследуем вопрос о структуре общего решения однородного линейного дифференциального уравнения, общий вид которогоОпределение. Всякая система из n линейно независимых решений о.л.д.у. n-го порядка называется фундаментальной системой решений (Ф.С.Р.) этого уравнения.
Замечание. Легко видеть, что фундаментальных систем решений бесконечно много, поскольку вместо нулей и единиц в качестве начальных значений для решений
Уь У2 9 • • • 9 Уп можно назначать любые числа, лишь бы определитель из этих чисел был отличен от нуля.
Т
где Q 9 С2, • • •, Ci
п
У - Сху\ + С2уг + ... + Спуп
произвольные постоянные.
еорема (о структуре общего решения о.л.д.у.). Если Уь У 2? ••• ? Уп - какая- нибудь фундаментальная система решений о.л.д.у. n-го порядка, то его общее решение имеет вид:Доказательство: 1) Согласно следствию из свойств множества решений
о.л.д.у. функция (2) является решением уравнения (1) при любых С\ ? ^2 •>'•'•> Сп .
2) Убедимся, что по формуле (2) путем выбора значений произвольных постоянных можно получить любое частное решение уравнения (1),
удовлетворяющее начальным условиям y(x0) = y0, y(хо) = у0, ..., y(n_1)(x0) = y0n_1), где хо е 1, а числа y0, у0 , ..., у0 - произвольны. Потребовав выполнение
U /Л \ U U
начальных условий для решения (2), получим систему линейных уравнений
'С\ У\ Со) + с2у2 Со) + • • • + с„у„ (х0 ) = у0,
С\У\ (х0) + С2у'2 (х0) +...+ Спу'„ (х0 ) = Уо,
V
с
относительно неизвестных
с с. Определитель этой системы равен
вронскиану линейно независимой системы решений Уъ У2 ? • • • ? Уп в точке *^0 и, т.к. система функций линейно независима, он отличен от нуля ^x0 е I. Поэтому по
правилу Крамера эта система имеет (притом единственное) решение, при котором функция (2) будет удовлетворять заданным начальным условиям. ■
Из доказанной теоремы следует, что задача отыскания общего решения о.л.д.у. n-го порядка сводится к нахождению любых n линейно независимых решений этого уравнения.
г3 v4
Пример. Проверить, что функции x и x являются решениями уравнения
x2 у" - 6xyf +12 у = 0
и найти его решение, удовлетворяющее начальным условиям у (1) = 1, у(1) = 2.
3 f 2 tt
◄ Подставив в уравнение У = x , у = 3х , у = 6x , получаем тождество:
6х3 - 18x3 +12x3 = 0 ^ 0 = 0.
Аналогично проверяется вторая функция. Данное уравнение является однородным линейным дифференциальным уравнением 2-го порядка (к виду (1) оно приводится
2
путем деления на x ); интервалы непрерывности коэффициентов - Л =(-сю,°) и
3 4 x3
12 = (0, +^). Так как решения x и x линейно независимы (^ ^ const), то они
образуют фундаментальную систему решений данного уравнения, и по теореме его общее решение имеет вид
y = Cj x3 + C2 x4.
После подстановки начальных значений x = 1, y = 1 и У = 2 в общее
решение и его производную У =3Cix +4C2x найдем C1 = 2 , C2 = _1, и, следовательно, искомое частное решение y = 2х^ _ Х . ►
Общий вид о.л.д.у. n-го порядка с постоянными коэффициентами
У{п) + аху{п~1) + ... + ап_ху' + апу = О
где ••• - некоторые числа, или короче ^00 — 0, если обозначить
через L линейный дифференциальный оператор с постоянными коэффициентами,
U U 1
действующий по формуле
и у) = у(п) + аху(‘п~1) + ... + ап_У + апу.
Определение 2. Многочлен n-й степени от переменной X
Р(7С) = У/1 + a{kn ^ + ... + ап_\К + ап
р
называется характеристическим многочленом, а алгебраическое уравнение n-й степени
-
У!1 + a{kn ^ + ... + ап_\К + ап — О
характеристическим уравнением для о.л.д.у.Теорема (о характеристическом уравнении). Функция e тогда и только тогда является решением о.л.д.у. с постоянными коэффициентами, когда X есть корень (действительный или комплексный) соответствующего характеристического уравнения.
Доказательство: Посмотрим, как оператор L действует на экспоненту ^, где X - произвольное число:
Це^) = (е^ )(п) +щ(еЪ:)("-,) + ...+а„_1(екс)'+а„е^ = = Ve'-' + а{Хп~1е^х + ... + ап_{Ке^х + апе^ = Р{ /. )е/л
Равенство L(ekx) — P(X)ehc означает, что всякая экспонента e оператором L переводится в пропорциональную ей функцию.
Пусть теперь y — eX°x. Тогда у - решение о.л.д.у. (3) о L(У) — 0 о P(X0)ex°x — 0
Общий вид о.л.д.у. 2-го порядка с постоянными коэффициентами:
У
+ а\У'
+ а2
У —
0
Его характеристическое уравнение является квадратным вида
У2 + а1 У, + а2 — 0
(6)
Пусть У1 и 'w 2 - корни характеристического уравнения. Рассмотрим три возможных случая.
л л
I. Если дискриминант уравнения (6) D > 0 . Числа У1 и У 2 действительны и
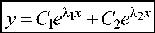
II. Если дискриминант уравнения (6) D — 0. Числа Л 1 иЛ 2
действительны и
.Лх
совпадают, т.е. корень Л — Л1 — Л2 - двукратный. Функция е является решением уравнения (5). Проверим, что другим решением этого уравнения в этом случае является
Лх
функция хе . Действительно, по теореме Виета Л1 + Л2 — 2Л — ~а1, так что двукратный корень Л удовлетворяет двум равенствам: Л + а1Л + а2 — 0 2Л + а1 — 0 . с учетом этих равенств, подставляя
у — хеЛ, у — (хв^У — (1 + Лх)еЛ и ух — (хвЛУ — (2Л + Л2х)вЛ
в уравнение (5), получим [2Л + а1 + х(Л + а1Л + а2)]е — 0, т.е. 0 0 .
и
Лх
.Лх
Решения е и хе линейно независимы и образуют, следовательно, фундаментальную систему решений, так что общее решение уравнения (5) в этом случае
у — вЛ (C1 + С2 х)
л л
III. Если дискриминант уравнения (6) D < 0. Числа ^1 и ^ 2 комплексно
сопряженные, т.е. ^1,2 — О — ip . Тогда одним из решений уравнения (5) согласно теореме 2 является комплексная функция
gV — е( О+Ф)X — еш cos рх + ieoc sin px
Заметим, что если y — u + iv - комплексное решение о.л.д.у. то u — Re y и v — Im y - его действительные решения, т.к. из L(u + w)— L(u) + iL(v)— 0 следует
L
У
— еОх
(C\ cos Px +
C2
sin px)
Пример. Найти общее решение уравнения
У" + 2 У' +10 у = 0.
Пример. Найти решение уравнения
У4 у = 0,
удовлетворяющее начальным условиям у (0) = 0, у '(0) = 4. Пример. Найти решение уравнения
у(4) + у" = 0
у
удовлетворяющее начальным условиям
(0) = у '"(0) = -1, у ' (0) = 1, у "(0) = 0Лекции 6-7. Неоднородные линейные дифференциальные уравнения.
Общий вид неоднородного линейного дифференциального уравнения:
у(п) + щ(х)у{п~Х) + ... + ап_\(х)у' + а„(х)у = Ь(х) ^
и
отлична от
(2)
ли, в краткой записи, L(y) _ b(x) (здесь правая часть b(x) тождественного нуля на интервале I).Для данного неоднородного уравнения (1) уравнение
у{п) + ах{х)у{п~Х) + ... + ап_х(х)у' + ап(х)у = О
/ W U \ U
(с той же левой частью) называется соответствующим однородным линейным дифференциальным уравнением.
Свойства множества решений неоднородного линейного дифференциального уравнения (н.л.д.у.):
1) если У\(x) - какое-нибудь решение н.л.д.у., а Уо(x) - какое-нибудь решение
соответствующего о.л.д.у., то их сумма yi + уо есть решение н.л.д.у.;
Доказательство: если yi( x) - решение уравнения (1), а уо(x) - решение
уравнения (2), то L(yi) = b(x), а L(yo) =0 на I; поэтому, ввиду линейности оператора L
L{ yi + Уо) = L( У1) + L( yo) = b( x) + 0 = b( x),
т.е. У\ + Уо - решение уравнения (1).
2) если У\(x) и У2(х) - какие-нибудь два решения н.л.д.у., то их разность yi -У2 есть решение соответствующего о.л.д.у.
Доказательство: если У1( х ) - решение уравнения (1), а Уо(х) - решение
уравнения (2), то L( = b( х), а L( Уо) = 0 на I; поэтому, ввиду линейности оператора
L
L(У1 + Уо) = L(У1) + L(Уо) = b(х) + 0 = b(х) ,
т.е. У1 + Уо - решение уравнения (1). Если же У1(х) и У2(х) - какие-нибудь решения уравнения (1), то
L(У1 - У2) = L(У1) - L(У2) = b(х) - b(х) = о , т.е. У1 - У2 - решение уравнения (2). ■
Из этих свойств следует
Теорема (о структуре общего решения н.л.д.у.). Общее решение н.л.д.у. равно сумме любого частного решения этого уравнения и общего решения соответствующего о.л.д.у.
Доказательство: Пусть У -любое фиксированное решение уравнения (1), а У О - общее решение уравнения (2). Тогда, во-первых, при любых значениях параметров
Q 5 С2,..., Сп 5 входящих в 3^0 , функция У ~ У У0 согласно первому свойству будет решением уравнения (1). С другой стороны, пусть У1 - произвольное частное решение уравнения (1). Согласно второму свойству разность у1 ~ У является
у-»»'
решением уравнения (2), а значит Л — У = У) или У\ = У + Уо при некоторых
значениях параметров Q, С2,..., СПг д эхо и означает, что функция У = У + У о является общим решением уравнения (1). ■
Пример. Проверить, что функция y = 32 — 2 является решением уравнения у"~ У - 2у = 1 — 6x и найти общее решение этого уравнения.
◄ Данное уравнение является н.л.д.у. 2-го порядка. Подставляя в него У = 3 x - 2
, у = 3 , у = 0 , получаем тождество 1 — 6х = 1 — 6х . Соответствующее о.л.д.у. имеет вид
У" — У — 2 у = 0.
Найдем его общее решение уо: характеристическое уравнение ^2 — ^ — 2 = 0 ; его
корни У1 =—1, ^2 = 2; фундаментальная система решений - у = e 2, у2 = ^2;
отсюда уо = Ce х + C2e2*. Складывая теперь данное частное решение н.л.д.у. и общее решение о.л.д.у., согласно теореме 1 получаем общее решение данного уравнения
у = Ce~х + C2e2x + 3x — 2 . ►
При решении неоднородных линейных дифференциальных уравнений бывает часто полезна также следующая теорема.
Теорема (принцип суперпозиции решений). Если правая часть н.л.д.у.
L(y) = b( х)
есть сумма двух функций, т.е.
b(х) = bi(х) + b2(х),
а У1(х) и У2(х) - какие-нибудь частные решения уравнений L( У) = bi( х) и L( У) = b2( х)
соответственно, то у1 + у2 есть решение исходного уравнения.
Доказательство: Ввиду линейности оператора L
L( У1 + У2) = L( У1) + L( У 2) = bi(х) + b2(х) = b( х),
т.е. У1 + У2 - решение уравнения L( У) = b( х). ■
Очевидно, теорема остается справедливой и в случае, когда правая часть н.л.д.у. является суммой нескольких функций.
Нахождение частного решения н.л.д.у.
Пусть n=2, т.е. н.л.д.у. имеет вид:
У " + а\( X) у' + «2 ( X ) у = b( x )
Метод вариации произвольных постоянных.
Будем искать частное решение У н.л.д.у.
в виде У ~ С\(х)У\ + С2М.У2, где У\ и У 2 - какая-нибудь фундаментальная система решений соответствующего о.л.д.у.
у" + « (x) у" + a2 (x) У = 0 , (4)
а Ci(x) и C2( x) - функции, подлежащие нахождению (этот вид получается, если в
выражении общего решения У = Qyi + C2 У2 уравнения (4) произвольные постоянные считать функциями от х - отсюда название метода).
Для того чтобы функция У была решением уравнения (3), достаточно, чтобы функции с1(x) и Q>(x) удовлетворяли системе из уравнений
га у + C2 У2 = 0,
|с!М+C2 y2= b( x). (7)
Эта система линейных уравнений относительно С1 и С2 имеет единственное решение, поскольку ее определитель является вронскианом фундаментальной
системы решений У1, У 2 и, следовательно, не равен нулю. Решив эту систему, далее
путем интегрирования найдем ci( x) и C2(x).
Пример 2. Найти общее решение уравнения
П
ех
x2 +1 •
о f ,У - 2У + У
◄ Найдем сначала общее решение y0 соответствующего однородного уравнения
У
Характеристическое уравнение отсюда
X2 - 2X +1 = 0
имеет двукратный корень
= Ь
 "
- 2у + У = 0 •
"
- 2у + У = 0 •
Уо = Qex + C2 xe*.
Ч астное
решение •'
данного
неоднородного уравнения найдем методом
вариации произвольных постоянных.
Полагаем
астное
решение •'
данного
неоднородного уравнения найдем методом
вариации произвольных постоянных.
Полагаем
у — Ci(x)ex + С2(х)хех.
Найдя yi = e и У2 = (1 + x)ex, составим систему уравнений (7) относительно Ci и
C2 :
'Ciex + C2 xex = 0,
C
x
x2 +1’ 1
iex + C2 (i + x )ex =x
c ; =
C' = —
решив которую, получим C1 x2 +1,
x2 +1. Путем интегрирования этих
равенств находим Ci(x) = — taVх1 +1, C2(x) = arctg x (для нахождения частного решения данного уравнения достаточно найти по одной из первообразных функций
Cf Cf
C1 и ^2 ). Следовательно,
у - -ех 1пл/х2 +1 + хех arctg х .
Складывая в заключение У О и У , получаем общее решение данного уравнения
y = ex (C1 + C2x -1nVx2 +1 + x arctg x). ►
2. Метод неопределенных коэффициентов для нахождения частного решения н.л.д.у. с постоянными коэффициентами
Рассмотрим уравнение 2-го порядка У + Py + ЧУ = b(x) с
характеристическим уравнением У2 + Ру + q = 0 соответствующего о.л.д.у.
з у
Обозначим у 1 ’ у 2 - корни характеристического уравнения.
I. Пусть b(x) = P(x)e<ax, где P( x) - многочлен n-й степени.
Тогда возможны следующие частные случаи:
а ^ У1 и а ^ У 2, т.е. число а не является корнем характеристического уравнения. Тогда частное решение следует искать в виде, аналогичном функции b( x)
, т.е. У = Q(x)ewc ? где
Q(x) — А§хп + А\ХП ^ +... + Ап ^3)
- некоторый многочлен той же n-й степени, записанный в общем виде, т.е. с неопределенными (буквенными) коэффициентами.
Подставляя У — Q(x)eax вместе со своими производными в уравнение
у" + py' + qy — b( x)
и приравнивая соответствующие коэффициенты, найдем
-^о? #
гг г д 3 x
Пример: Решить уравнение у + у — 2у — e
Ад ^ ^2 и а = ^1 или а — ^2, т.е. а - простой (однократный) корень характеристического уравнения. Частное решение следует искать в виде
у
некоторый многочлен той же n-й
— xQ(x)ecuc 5 где многочлен в(х) степени, записанный в общем виде.П
—2
xример: Решить уравнение у + у — 2у — e
а — ^1 2, т.е. а - двукратный корень характеристического уравнения.
Частное решение следует искать в виде У = x2Q(x)eax ? Где Q(x) некоторый многочлен той же n-й степени, записанный в общем виде.
Пример: Решить уравнение у + у — 2у — 5xe Пример 3. Найти общее решение уравнения
у" + у' — 2 у — ex (6x + 2).
Пусть b(х) — (р(x)cosрх + p(x)sinPx)eQX, Где Pi(x) и P2(x) - многочлены.
Возможны следующие два частных случая:
Комплексное число /р не является корнем характеристического
уравнения. Тогда частное решение ищется в виде, аналогичном b(х), т.е.
У — (Q[(x)cos^x + Q2(x)sm^x)eax 5 где 01 (х) и Qi(x) - многочлены одинаковой
степени, равной высшей из степеней многочленов Pi(х) и P2(х), записанные в общем виде (т.е. с неопределенными (буквенными) коэффициентами).
Число ^ + /р является корнем характеристического уравнения. Тогда
у = x(Qi (х) cos Рх + Q2 (х) sin ^>х)еах.
Пример 4. Найти решение уравнения
y" — 4y' + 4y — 8sin2 х,
Пример 5. Найти общее решение уравнения У" + У — 2(cos х — 5е 3х).
Лекция 8. Системы дифференциальных уравнений
Основные понятия
Определение. Система дифференциальных уравнений вида
У\ =А(х,У1,У2,
У2= Л(Х,У1,У2, ".,У„)>
Уп fn У1’ У2’ •••5Уп)’
связывающая независимую переменную х, искомые функции XiM ? у2(х) ? ... ,у„(х) 5 и их производные 1-го порядка, и разрешенная относительно этих производных, называется нормальной системой.
Определение. Порядком системы дифференциальных уравнений называется сумма порядков уравнений, входящих в систему.
Определение. Решением (частным решением) системы (1) на интервале I
называется всякая совокупность (система) n функций У\ -9i(*), У2 = ФгООэ ••• >Уп = ФяМ, при подстановке которых в систему вместе с их производными каждое уравнение системы обращается в тождество относительно х е I.
Пример. Показать, что функции У1 , У2 =-У2Гх являются решением
системы
н
v' - У22
y2- л
y[=- У 2,
а (°»+да) .◄ Подставляя yi - Jx , yl - /2JX, y2 -- )2^/X, y2 - У\х1Х в данную систему,
получаем тождества /242- /242 и У\х4Х - XxVX при x е(0, +да) . ►
Определение. Равенства вида
У\(хо)=У\, У2(х0) = У2, ■■■,Уп(хо)=Уп (2)
(используется также запись У\ 1х=х0 = У\ , У2 L=x0 = Уг , • • • ?Уп L=x0 = Уп), где
хо>УиУъ --чУп - заданные числа (начальные значения), называются начальными условиями для системы (1).
Определение. Задача отыскания решения системы (1), удовлетворяющего заданным начальным условиям (2), называется задачей Коши для этой системы.
Теорема (существования и единственности решения задачи Коши для системы
(1)). Если функции /ъ/2? •••>/« и их частные производные дуj , Uj = h 2,... ,п 5
непрерывны в некоторой области D a Rn+l , то для любой точки (х0,у?,у\,... ,у°) е D задача Коши для системы (1) с начальными условиями (2) имеет и притом единственное решение.
Определение. Совокупность n функций
У\ ф^^С • • • ? ^77)? У2 Ф2<Х * * * ? ^77)? • • • ? .У77 Ф^(*^5 ^Л? * * *? ^77 ) , (3)
зависящих от п параметров СЪС2, ...,СИ? называется общим решением системы (1), если:
при любых допустимых значениях СЬС2,... ,С„ она является решением этой системы;
любое частное решение системы может быть получено из (3) при некоторых значениях параметров Q, С2,..., Сп.
Второе условие означает, что для любой точки (x0,yi°,y2, еО найдутся
такие значения СЬС2, ...,СИ? при которых функции (3) будут удовлетворять начальным условиям (2)).
Пример. Показать, что совокупность функций
у
2 C2 е3
= Ci е—* + C2 е3х, г = 2 Cx e-xя
<
v
у' = У — г
z' = z — 4 у.
вляется общим решением системыНайти частное решение этой системы, удовлетворяющее начальным условиям у(0) = — 1, z(0) = 2.
◄ Проверим выполнение условий из определения общего решения.
1) Число произвольных постоянных в функциях данной совокупности равно двум, что совпадает с порядком системы. При любых значениях с и С2 функции у и z образуют решение системы:
У
<
= Ce -х + C2e3 *, ^ I y' = C - * + 3С2в3х,z = 2Cje“х - 2C2e3х [Z = -2Cie- - 6C2e3x;
подставляя в данную систему у, z, У' и z', получим тождества:
-C1e~х + XC2e3x = C1e~х + C2e3х - (2C1e-х - 2C2eXx), -2C1e-х - 6C2e3x = 2C1e-х - 2C2exх - 4(C1e-х + С^х)
-C1e -х + 3C2e3 х = -C1e ~х + 3C2e3 х,
-2C1e-х - 6C2e3х = -2C1e“х - 6C2e3х •
2) Каковы бы ни были начальные значения х0, y0, z0 , система уравнений
У
имеет, притом единственное решение относительно с и C2, т.к. ее определитель А =
е~хо е3хо
2 e - х0 -2 в3хо
= -4 e2 хо * 0 С С,
, и, следовательно, существуют значения ^1 и ^2 ,
о = Qe-х0 + C2e3 хо, z0 = 2C1e-хо - 2C2г3хопри которых данные функции будут удовлетворять начальным условиям y(xo) - уо,
z (Хо) - Zo .
Поскольку все условия определения общего решения выполнены, то данная совокупность функций является общим решением данной системы.
Для нахождения частного решения после подстановки начальных значений x — 0 , y — -1 и z — 2 в общее решение получим систему
г-1 — Q + C2,
[2 — 2Ci - 2C2,
откуда Ci — 0, C2 —-1 и, следовательно, искомое частное решение есть y — -e3x,
Z — 2e3x. ►
Сведение уравнения n-го порядка к нормальной системе
Дифференциальное уравнение n-го порядка
У») = Дх, 7,У»-1)),
разрешенное относительно старшей производной, можно свести к нормальной системе n-го порядка. Для этого введем новые функции
У\ = У, У2=у', ••• , Уп=У(п~Х).
Тогда данное уравнение, очевидно, эквивалентно следующей нормальной системе n- го порядка:
' yl = У2,
y2 = Уэ,
<
У =/(х,У\,У2, •••,УпX
которая является частным случаем системы (1).
Пример 3. Привести к нормальной системе дифференциальное уравнение
y" + xy'-У2 = 0.
◄ Положим z = y . Тогда z 1 = y" и уравнение приводится к нормальной системе
| У = z ,
[ z ' = y2 - xz. ►
Метод исключения
Одним из методов решения системы дифференциальных уравнений является метод исключения. Он основан на обратном переходе - сведении системы к одному дифференциальному уравнению относительно одной из неизвестных функций. Например, для решения нормальной системы второго порядка
У\ — f\( X Уъ У2Х У'г = f2( X Уь У2)»
в
<
ыражаем из первого уравнения y2 = g(x, y\, у1) , после чего, находя полнуюФ’2
производную dx и подставляя эти выражения во второе уравнение, получаем
уравнение 2-го порядка относительно функции У\ .
Пример 4. Решить методом исключения систему
<
◄ Выразим из первого уравнения z: z — У — У . Отсюда z — У — У . Подставив эти выражения во второе уравнение системы, получим уравнение 2-го порядка относительно у:
У — У — У — У — 4У или У 1 — 2У' — 3у — 0 .
Общее решение этого о.л.д.у. с постоянными коэффициентами имеет вид
У — Cl e—х + C2 e3x.
Отсюда У — —Cie х + ЗС2еЪх и
z
— 2C2e3x.
— У — У — Cxe~x + C2e3x — (—Cex + 3C2e3x ) — 2Cie—xТ
г
<
y — Ci e -x + C2 e3 x, z — 2 C1 e~x — 2 C2 e3 x
- общее решение данной системы. ►
аким образом,Определение. Однородной линейной системой дифференциальных уравнений (о.л.с.д.у.) n-го порядка называется нормальная система вида
Х\ = ап (/) Xi + а\2 {t)x 2 + ... + а\п (t)x}
*2 = «21 (0*1 + «22(0*2 + ••• + «2и(0*,
х
(4)
„ = «„i(0*i + «„2 (0*2 + • • • + dnn(t)xnКоэффициенты a (t) предполагаются далее непрерывными функциями на некотором интервале I.
Е
A( t) =
rau(t) al2(t)... abl(t) ^ a2i(t) a22(t) ■ ■ ■ a2n(t)
(матрица системы),
V^nl(0 ^л2(0 ••• ®nn it))
X =
V xn J
\X„J
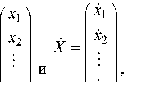 сли
ввести матрицы
сли
ввести матрицы
то равенство
X = A{t)X
есть матричная запись системы (4).
Произвольное решение системы (4) можно записать в виде матрицы-столбца (n- компонентной вектор-функции)
(
Свойства множества решений о.л.с.д.у.:
если х i(t) и X2( О - какие-нибудь два решения о.л.с.д.у., то их сумма х i + х2 также есть решение этой системы;
если х(t) - какое-нибудь решение о.л.с.д.у. и C - любое число, то их произведение сх также есть решение этой системы.
Следствие. Если ХъХ2,...,Хт - решения о.л.с.д.у. и СъС2,...,Ст _
произвольные числа, то вектор-функция С\х\ + С2Х2 +... + СтХт также является решением этой системы.
Система вектор-функций х\ (О? Х2 (0? • • • ? Хт (О называется линейно
независимой на промежутке I, если из равенства
С
Vt е I
хХх + С2Х2 +... + СтХт - О(здесь 0 _ нулевой столбец) следует, что Q — С2 - • • • - Ст — О
Пусть дана система Xx(t),X2{t),...,Xn{t) из ^-компонентных вектор-функций. Если образовать квадратную матрицу из этих вектор-функций, сделав их ее столбцами, то определитель W (t) этой матрицы называется вронскианом данной системы.
Теорема (необходимое и достаточное условие линейной независимости решений о.л.с.д.у.). Для того чтобы п решений ХЬХ2, однородной линейной системы
дифференциальных уравнений n-го порядка были линейно независимы на интервале I непрерывности коэффициентов этой системы необходимо и достаточно, чтобы их вронскиан W (t) не обращался в нуль на этом интервале.
Определение. Всякая совокупность из n линейно независимых решений о.л.с.д.у. n-го порядка называется фундаментальной системой решений этой системы.
Теорема (о структуре общего решения о.л.с.д.у.). Если ХЪХ2,... ,Хп - какая- нибудь фундаментальная система решений о.л.с.д.у. n-го порядка, то ее общее решение имеет вид:
Х = С1Х1+С2Х2+ ...+СпХп, (2)
где Ci,C2,... ,Сп - произвольные постоянные.
