§9. Схема Бернулли.
9.1. Основные определения.
Из урны, в которой
лежат две буквы
и
,
последовательно с
возвращением
вытаскивают
одну букву и раскладывают вытащенные
буквы по порядку в ряд. Получается слово
из букв
и
,
которое является размещением с
повторениями
из двух элементов по
элементов. Это слово объявляется
элементарным
событием.
Из комбинаторики следует, что число
всех элементарных событий равно
.
Будем вводить
вероятность события, пользуясь
классической вероятностной схемой с
неравновозможными
исходами.
Для этого достаточно ввести вероятности
элементарных событий
,
.
Подробно опишем этот процесс, предполагая
для простоты, что
.
Предположим, что задано число
,
такое, что
и пусть
.
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
Так как
,
то новая вероятностная схема с неравновозможными исходами имеет право на существование. Она называется схемой Бернулли или биномиальной схемой. Совершенно аналогично эта схема определяется при любом .
Пример.9.1. Найти вероятность того, что буква будет вытащена последней, если .
Решение.
Введем событие
,
которое наступает тогда и только тогда,
когда последней будет вытащена буква
.
Ясно, что
.
.
9.2. Две основные вероятности в схеме Бернулли и их классическая интерпретация.
Определение. Событие состоит из всех элементарных событий, в которых буква встречается ровно раз.
Определение.
Событие
состоит из
всех элементарных событий, в которых
буква
встречается от
раз до
раз включительно,
.
Теорема 9.1. Верно равенство
,
где
.
Теорема 9.2. Верно равенство
.
Классическая
интерпретация вероятности
.
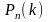Вероятность того, что в независимых испытаниях, в каждом из которых вероятность события равна , событие наступит ровно раз (безразлично в какой последовательности) равна .
Классическая
интерпретация вероятности
.
Вероятность того, что в независимых испытаниях ,в каждом из которых вероятность события равна , событие наступит от раз до раз включительно (безразлично в какой последовательности) равна .
Пример 9.2 . Вероятность попадания в цель при одном выстреле равна 0,7. Произвели 8 выстрелов независимо друг от друга. Найти вероятности событий: а) в цель попали ровно 5 пуль; б) в цель попали не менее 5 пуль;
в) в цель попали не менее двух, но не более четырех пуль.
Решение.
Применяется схема
Бернулли:
число
независимых испытаний (выстрелов);
вероятность
попадания при каждом выстреле,
.
а) Вероятность того, что в цель попали ровно 5 пуль, равна
.
б) Вероятность того, что в цель попали не менее 5 пуль, равна
.
в) Вероятность
того, что в цель попали не менее двух,
но не более четырех пуль равна
.