Вариант 1

1. Для функции у=х² +8х+ 12. Найдите:

а) значение у при х = –3,5;

б) нули функции;

в) координаты вершины параболы;

г) постройте график;

д) по графику определите свойства функции – D(y), E(y), промежутки возрастания/убывания,

у> 0, у < 0.

2. Найдите наибольшее значение функции

у=–3х² – 12х – 5.

3. Найдите область значений функции

у=х² + 2х – 3, где x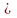 [–3; 2].

4. Без построения, определите, пересекаются ли парабола у =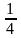 х² и прямая у= –3–2х. Если точки пересечения существуют, то найдите их координаты.

Вариант 2

1. Для функции у=–х² – 8х–12. Найдите:

а) значение у при х = 1,5;

б) нули функции;

в) координаты вершины параболы;

г) постройте график;

д) по графику определите свойства функции – D(y), E(y), промежутки возрастания/убывания,

у> 0, у < 0.

2. Найдите наибольшее значение функции

у=–х² + 6х – 4.

3. Найдите область значений функции

у=х² – 4х – 7, где x [–2; 7].

4. Без построения, определите, пересекаются ли парабола у = х² и прямая у=20–3х. Если точки пересечения существуют, то найдите их координаты.

Вариант 3

1. Для функции у=–х² +4х– 3. Найдите:

а) значение у при х = 0,3;

б) нули функции;

в) координаты вершины параболы;

г) постройте график;

д) по графику определите свойства функции – D(y), E(y), промежутки возрастания/убывания,

у> 0, у < 0.

2. Найдите наименьшее значение функции

у=х² – 4х + 1.

3. Найдите область значений функции

у=–3х² +12х – 8, где x [–1; 4].

4. Без построения, определите, пересекаются ли парабола у = х² и прямая у=2х–1,5. Если точки пересечения существуют, то найдите их координаты.

Вариант 4

1. Для функции у= –х² + 6х– 8. Найдите:

а) значение у при х = 1,2;

б) нули функции;

в) координаты вершины параболы;

г) постройте график;

д) по графику определите свойства функции – D(y), E(y), промежутки возрастания/убывания,

у> 0, у < 0.

2. Найдите наибольшее значение функции

у=–х² –4х + 1.

3. Найдите область значений функции

у=3х² – 6х + 2, где x [–1; 5].

4. Без построения, определите, пересекаются ли парабола у = х² и прямая у = –4+3х. Если точки пересечения существуют, то найдите их координаты.

Вариант 5

1. Для функции у=х² +10х+ 24. Найдите:

а) значение у при х = –4,5;

б) нули функции;

в) координаты вершины параболы;

г) постройте график;

д) по графику определите свойства функции – D(y), E(y), промежутки возрастания/убывания,

у> 0, у < 0.

2. Найдите наименьшее значение функции

у=2х² – 4х + 5.

3. Найдите область значений функции

у=х² – 2х – 8, где x [–3; 3].

4. Без построения, определите, пересекаются ли парабола у = х² и прямая у= –5х–12. Если точки пересечения существуют, то найдите их координаты.

Вариант 6

1. Для функции у=х² – 6х+ 5. Найдите:

а) значение у при х = 0,5;

б) нули функции;

в) координаты вершины параболы;

г) постройте график;

д) по графику определите свойства функции – D(y), E(y), промежутки возрастания/убывания,

у> 0, у < 0.

2. Найдите наименьшее значение функции

у=х² – 8х + 7.

3. Найдите область значений функции

у=х² – 6х – 13, где x [–1; 5].

4. Без построения, определите, пересекаются ли парабола у = х² и прямая у=5х–16. Если точки пересечения существуют, то найдите их координаты.

Вариант 7

1. Для функции у= –х² + 8х+15. Найдите:

а) значение у при х = –3,5;

б) нули функции;

в) координаты вершины параболы;

г) постройте график;

д) по графику определите свойства функции – D(y), E(y), промежутки возрастания/убывания,

у> 0, у < 0.

2. Найдите наименьшее значение функции

у=2х² – 8х + 11.

3. Найдите область значений функции

у=–х² +10х – 24, где x [–7; 2].

4. Без построения, определите, пересекаются ли парабола у = х² и прямая у = 4х+7,5. Если точки пересечения существуют, то найдите их координаты.

Вариант 8

1. Для функции у= – х² – 6х –5. Найдите:

а) значение у при х = – 1,2;

б) нули функции;

в) координаты вершины параболы;

г) постройте график;

д) по графику определите свойства функции – D(y), E(y), промежутки возрастания/убывания,

у> 0, у < 0.