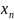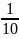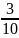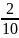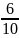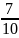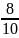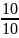- •Функции от случайных величин.
- •Многомерные законы распределения. Функции от св.
- •Критерии независимости.
- •Занятие 4. Зависимые случайные величины. Числовые характеристики случайных векторов.
- •Свойства Математического ожидания и дисперсии.
- •Гауссовский случайный вектор
- •Свойства нормального вектора ( ).
- •Занятие 5. Центральная предельная теорема и збч.
- •Занятие 6. Точечные оценки параметров. Метод моментов.
- •Метод максимального правдоподобия.
- •Задачи для решения в аудитории
- •Задачи для самостоятельного решения
- •Доверительные интервалы
- •Принцип построения доверительных интервалов:
- •Построение доверительных интервалов для параметров нормального распределения
- •Проверка гипотезы о независимости признаков
- •Данные в прилагаемом файле.
Свойства нормального вектора ( ).
Распределения компонент нормального вектора нормальны, причем
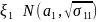 ,
,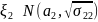 .
.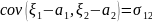 ,
,
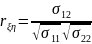 .
.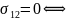
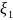 и
и
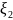 независимы.
независимы.
То есть для нормальных CB некоррелируемость эквивалентна независимости.
Если
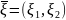 – нормальный случайный вектор, то
распределение случайной величины
– нормальный случайный вектор, то
распределение случайной величины
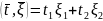 нормальное (или вырожденное) для
произвольного
нормальное (или вырожденное) для
произвольного
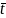 .
(Обратное
утверждение тоже верно: если для
произвольного постоянного вектора
распределение случайной величины
нормальное (или вырожденное), то
– нормальный случайный вектор.)
.
(Обратное
утверждение тоже верно: если для
произвольного постоянного вектора
распределение случайной величины
нормальное (или вырожденное), то
– нормальный случайный вектор.)Условные плотности распределения
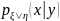 и
и
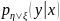 – нормальны.
– нормальны.(Теорема о нормальной корреляции) Если двумерная СВ
 X
X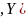 распределена
по нормальному закону, то
и
связаны линейной корреляционной
зависимостью:
распределена
по нормальному закону, то
и
связаны линейной корреляционной
зависимостью:
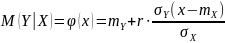 ,
,
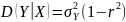 ;
;
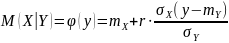 ,
,
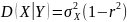 .
.
Задача 3. Пусть дан нормальный случайный вектор с параметрами
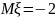 ,
,
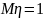 ,
,
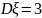 ,
,
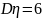 ,
,
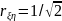 . Найдите закон распределения
. Найдите закон распределения
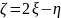 .
.
Решение. Согласно свойству 5, распределение нормально. Найдем параметры, используя свойства математического ожидания и дисперсии.
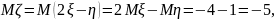
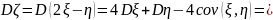
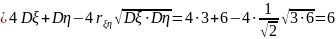 .
.
Выпишем
плотность:
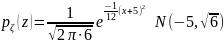 .
.
Занятие 5. Центральная предельная теорема и збч.
Теорема
1 (неравенства Чебышева). Для
любого
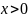 имеют место неравенства:
имеют место неравенства:
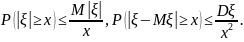
Доказательство.
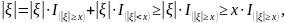
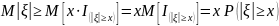
Второе
неравенство получается из первого
подстановкой
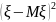 вместо
:
вместо
:
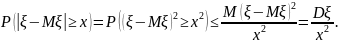
Следствие.
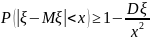
Теорема
2 (закон больших чисел Чебышева). Пусть
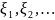 - независимые случайные величины и
существует такая константа
- независимые случайные величины и
существует такая константа
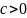 ,
что все
,
что все
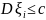 ,
,
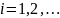
Тогда
при любом
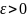
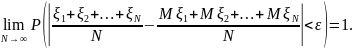
Доказательство.
Если
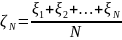 ,
то
,
то
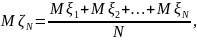
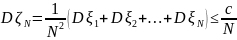 .
Следовательно,
.
Следовательно,
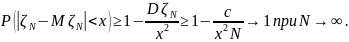
Теорема
3 (ЦПТ). Если
случайные величины
- независимы, одинаково распределены и
имеют конечные
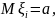
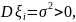 то
то
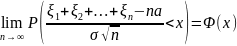
Задача 1. Имеется 100 квадратов, сторона которых может принимать значения 0.5 или 1 с вероятностями 0.3 и 0.7 соответственно. С какой вероятностью суммарная площадь всех квадратов будет в пределах от 750 до 805?
Решение.
Рассмотрим независимые
случайные
величины
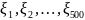 ,
распределенные по закону:
,
распределенные по закону:
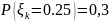 ,
,
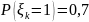 .
.
Тогда
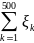 имеет смысл суммарной площади.
Воспользуемся ЦПТ:
имеет смысл суммарной площади.
Воспользуемся ЦПТ:
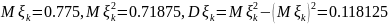
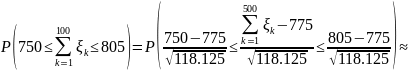
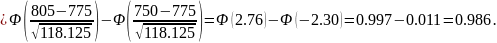
Задача 2. Театр на 1000 зрительских мест имеет два входа. Около каждого входа имеется свой гардероб. Предполагается, что зрители приходят в театр парами и с вероятностью 0,7 выбирают первый вход. Сколько мест должно быть в гардеробе у второго входа, чтобы в 95 случаях из 100 зрители, вошедшие через этот вход, могли сдать верхнюю одежду в ближайший гардероб?
Решение.
Рассмотрим независимые
случайные
величины
,
распределенные по закону:
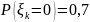 ,
,
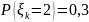 .
.
Тогда
нужно найти такое
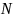 ,
что
,
что
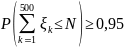 .
.
Воспользуемся
ЦПТ:
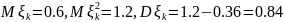
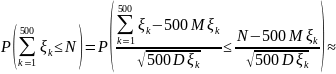
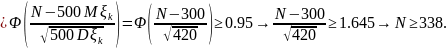
Задача 3. Урожайность куста картофеля равна 0 кг с вероятностью 0,1, 1 кг с вероятностью 0,2, 1,5 кг с вероятностью 0,2, 2 кг с вероятностью 0,3 и 2,5 кг с вероятностью 0,2. Какое наименьшее число клубней надо посадить, чтобы с вероятностью не менее 0,975 урожай был не менее 1 тонны?
Решение.
Рассмотрим независимые
случайные
величины
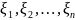 ,
распределенные по закону:
,
распределенные по закону:
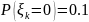 ,
,
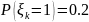 ,
,
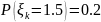 ,
,
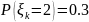 ,
,
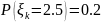
Тогда
нужно найти такое
,
что
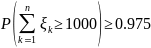 .
.
Воспользуемся
ЦПТ:
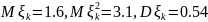
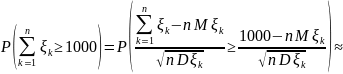
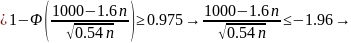
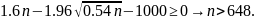
Задача 4. В поселке 2500 жителей. Каждый из них примерно 6 раз в месяц ездит в город на поезде, который ходит раз в сутки. Какой наименьшей вместимостью должен обладать поезд, чтобы он переполнялся в среднем не чаще, чем 1 раз в 100 дней?
Решение.
Рассмотрим независимые
случайные
величины
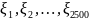 ,
распределенные по закону:
,
распределенные по закону:
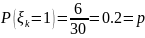 ,
,
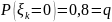 ,
,
Тогда
нужно найти такое
,
что
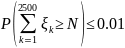 .
.
Воспользуемся
ЦПТ:
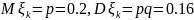
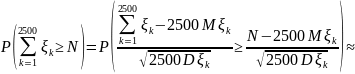
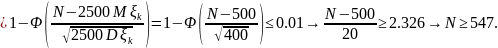
Задача
5.
Вероятность некоторого события
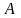 равна
равна
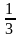 .
Производится
.
Производится
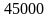 независимых опытов. Каково срединное
отклонение
независимых опытов. Каково срединное
отклонение
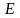 числа появлений события
от математического ожидания этого
числа?
числа появлений события
от математического ожидания этого
числа?
Решение.
Пусть
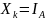 ,
тогда
,
тогда
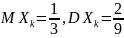 ,
,
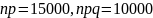 .
Используем теорему 3 и правило трех
сигм:
.
Используем теорему 3 и правило трех
сигм:
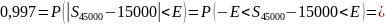
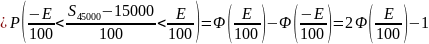
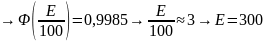
Ответ.
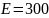
Задача №1 (ДЗ№4).Первоначальная обработка статистических данных.
Определение 1. Все значения, которые может принимать случайная величина , называют выборочным пространством, или генеральной совокупностью.
Выборкой объема называют возможных значений случайной величины:
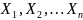 -
реализация выборки.
-
реализация выборки.
Определение 2. Статистикой, называется любая функция от выборки, не зависящая от неизвестных параметров распределения.
Примеры.
1)
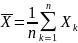 -
выборочное среднее
-
выборочное среднее
(или
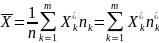 -
для статистического ряда)
-
для статистического ряда)
2)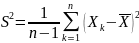 –
выборочная дисперсия
–
выборочная дисперсия
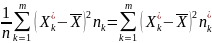 -
для статистического ряда
-
для статистического ряда
Определение
3.
Если выборку упорядочить в порядке
возрастания, то получим вариационный
ряд:
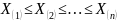 ;
при этом
;
при этом
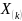 -
-
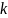 -ая
порядковая статистика
-ая
порядковая статистика
3) - статистика (функция от выборки)
Рассмотрим вариационный ряд , построенный по выборке
из
распределения
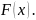
Теорема
1.
Если независимая выборка взята из
генеральной совокупности с функцией
распределения
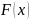 ,
то функции распределения крайних членов
вариационного ряда и их совместная
функция распределения имеют вид:
,
то функции распределения крайних членов
вариационного ряда и их совместная
функция распределения имеют вид:
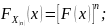
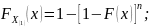
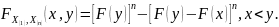
Доказательство. По определению функции распределения и в силу независимости выборки получаем:
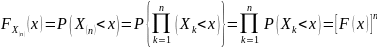 .
.
Аналогично,
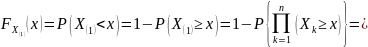
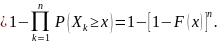
Далее,
в предположении
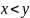 находим, что
находим, что
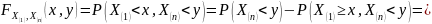
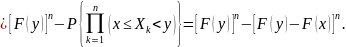
Определение 4. Выборочной функцией распределения называется
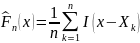 ,
,
,
,
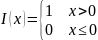 ,
,
То
есть
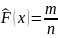 ,
если ровно
,
если ровно
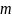 наблюденных значений меньше
.
наблюденных значений меньше
.
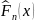 -
статистика (при каждом
),
то есть функция от выборки
-
статистика (при каждом
),
то есть функция от выборки
Пример. Рассмотрим выборку: 1,3,4,6,3,1,7,2,3,7
Строим статистический ряд и находим эмпирическую функцию распределения:
|
1 |
2 |
3 |
4 |
6 |
7 |
Относительные частоты |
|
|
|
|
|
|
Относительные накопленные частоты |
|
|
|
|
|
|
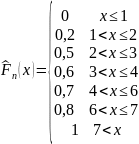
Теорема
2.
Если взята выборка объема
из генеральной совокупности, имеющей
функцию распределения
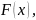 то
то
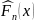 дискретная случайная величина, закон
распределения которой имеет вид:
дискретная случайная величина, закон
распределения которой имеет вид:
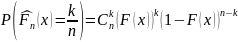 ,
,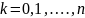
Доказательство.
При каждом
индикаторы
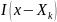 – независимые случайные величины с
законом распределения:
– независимые случайные величины с
законом распределения:
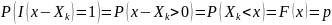
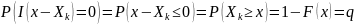
Следовательно,
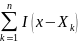 –распределена по закону Бернулли, то
есть
–распределена по закону Бернулли, то
есть
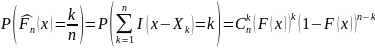 .
.
Задача 1. Первоначальная обработка статистических данных
По данной выборке
1. Найдите крайние члены вариационного ряда и размах выборки
2. Осуществите группировку данных (количество интервалов находим по правилу Стерджеса)
3. По сгруппированным данным постройте гистограмму относительных частот
4. Найдите эмпирическую функцию распределения и постройте ее график
5. Вычислите выборочное среднее и выборочную дисперсию.
Пример выполнения задания в среде MATHCAD и оформления работы в прилагаемом файле.