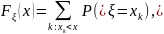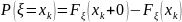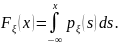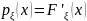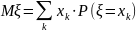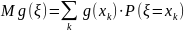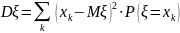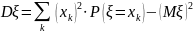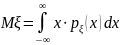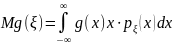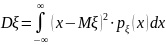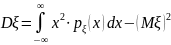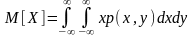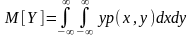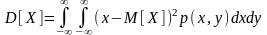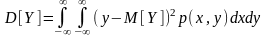- •Функции от случайных величин.
- •Многомерные законы распределения. Функции от св.
- •Критерии независимости.
- •Занятие 4. Зависимые случайные величины. Числовые характеристики случайных векторов.
- •Свойства Математического ожидания и дисперсии.
- •Гауссовский случайный вектор
- •Свойства нормального вектора ( ).
- •Занятие 5. Центральная предельная теорема и збч.
- •Занятие 6. Точечные оценки параметров. Метод моментов.
- •Метод максимального правдоподобия.
- •Задачи для решения в аудитории
- •Задачи для самостоятельного решения
- •Доверительные интервалы
- •Принцип построения доверительных интервалов:
- •Построение доверительных интервалов для параметров нормального распределения
- •Проверка гипотезы о независимости признаков
- •Данные в прилагаемом файле.
Практика ТВиМС (3 семестр) 2016-17
Занятие 1. Абсолютно непрерывные случайные величины и их характеристики. Функции от случайных величин.
Абсолютно
непрерывная случайная величина
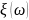 принимает значения в подмножестве
множества действительных чисел, и ее
закон распределения задается плотностью
вероятностей
принимает значения в подмножестве
множества действительных чисел, и ее
закон распределения задается плотностью
вероятностей
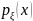 так, что вероятности
так, что вероятности
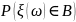
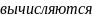 как
интеграл от
как
интеграл от
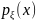 по множеству
по множеству
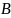 :
:
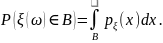 При
этом от функции плотности требуется
выполнение естественных свойств:
При
этом от функции плотности требуется
выполнение естественных свойств:
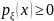 ,
,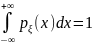 .
.
Определение.
Функцией распределения случайной
величиной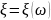 называют
называют
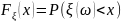 .
.
Свойства
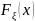 .
.
определена для всех значений
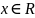 ,
непрерывна слева и не убывает.
,
непрерывна слева и не убывает.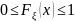 ,
причем
,
причем
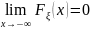 ,
,
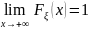 .
.Функция распределения однозначно определяет закон распределения случайной величины
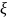 и однозначно определяется законом
распределения:
и однозначно определяется законом
распределения:
СВДТ |
|
|
СВНТ |
|
|
Определения числовых характеристик случайных величин для удобства дадим в виде таблицы.
|
Математическое ожидание |
Математическое ожидание функции от СВ |
Дисперсия |
СВДТ |
|
|
|
СВНТ |
|
|
|
Задача
1. Время ожидания у бензоколонки
заправочной станции является случайной
величиной
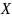 ,
распределенной по показательному закону
со средним временем ожидания
,
распределенной по показательному закону
со средним временем ожидания
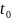 .
Найти вероятности следующих событий:
.
Найти вероятности следующих событий:
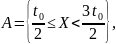
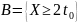 .
.
Решение.
Плотность распределения вероятностей
для показательного закона имеет вид
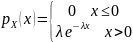 ,
где
,
где
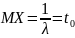 .
Тогда
.
Тогда
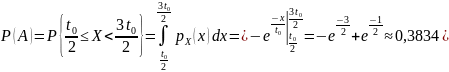 ,
,
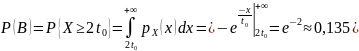 .
.
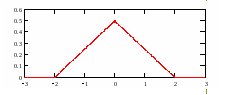 Задача
2. Случайная величина
распределена по закону Симпсона в
интервале
Задача
2. Случайная величина
распределена по закону Симпсона в
интервале
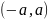 (на рисунке
(на рисунке
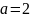 ).
Написать выражение для плотности
,
вычислить функцию распределения
,
математическое ожидание
).
Написать выражение для плотности
,
вычислить функцию распределения
,
математическое ожидание
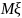 ,
дисперсию
,
дисперсию
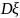 и среднеквадратичное отклонение (с.к.о.)
и среднеквадратичное отклонение (с.к.о.)
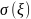 .
.
Решение. Выражение для плотности получим, выписывая уравнения прямых:
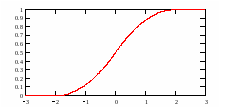
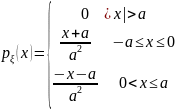 .
.
Вычисляем
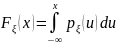 .
.
При

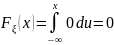 ,
,
при
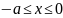
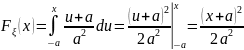 ,
,
при
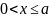
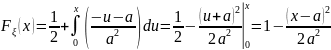 ,
,
при
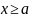
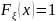 .
.
То
есть
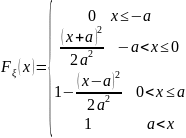 .
.
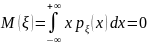
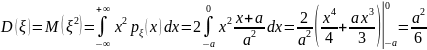
 .
.
Задача
3. При стрельбе по плоской мишени
расстояние
от точки попадания до центра распределено
по закону Рэлея с плотностью распределения
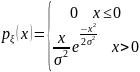 ,
где
,
где
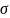 -
параметр, характеризующий распределение.
Построить эскиз графика
и вычислить
,
и
.
-
параметр, характеризующий распределение.
Построить эскиз графика
и вычислить
,
и
.
Ответ.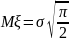 ,
,
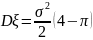 ,
,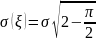 .
.
Задача
4. Скорость
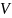 молекул идеального газа, находящегося
в равновесии при определенной температуре,
является случайной величиной,
распределенной по закону Максвелла с
плотностью
молекул идеального газа, находящегося
в равновесии при определенной температуре,
является случайной величиной,
распределенной по закону Максвелла с
плотностью
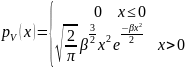 .
Найти среднее значение и дисперсию
.
.
Найти среднее значение и дисперсию
.
Ответ.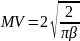 ,
,
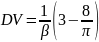 .
.
Функции от случайных величин.
Теорема.
Если случайная величина
имеет плотность распределения
,
а
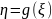 ,
где
,
где
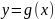 монотонная дифференцируемая (на множестве
значений
)
функция, то плотность случайной величины
монотонная дифференцируемая (на множестве
значений
)
функция, то плотность случайной величины
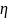 может быть вычислена по формуле:
может быть вычислена по формуле:
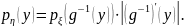
Задача
5. Найти закон распределения случайной
величины
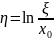 , если случайная величина
распределена по закону Парето с
параметрами
, если случайная величина
распределена по закону Парето с
параметрами
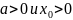 .
.
Решение.
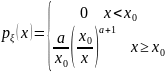 .
.
Согласно
общей формуле
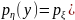 для монотонно возрастающей
для монотонно возрастающей
функции
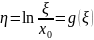 .
Находим обратную функцию:
.
Находим обратную функцию:
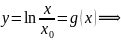
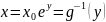 и
ее производную
и
ее производную
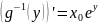 .
Пересчитываем плотность:
.
Пересчитываем плотность:
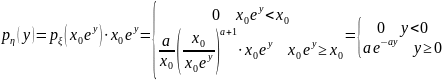 .
.
То
есть случайная величина
распределена по показательному закону
с параметром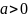
Задача
6. Найти плотность распределения
случайной величины
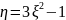 ,
если
,
если
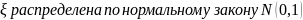 .
.
Решение.
Воспользуемся соотношением
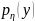 =
=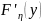 .
Выразим
.
Выразим
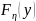 через
.
По определению
через
.
По определению
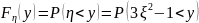 =
=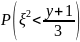 .
.
Если
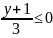
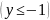 , то
, то
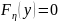 ,
а значит и
=0.
,
а значит и
=0.Если
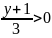
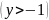 , то
, то
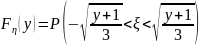 =
=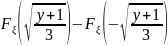 .
.
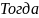 =
=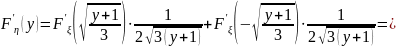
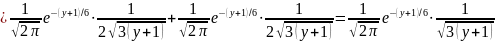 ,
,
 поскольку
поскольку
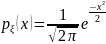 .
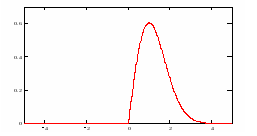
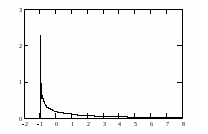
График функции
.
График функции
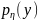 приведен на рисунке.
приведен на рисунке.
Задача
7. Случайная величина
распределена по показательному закону
с параметром
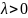 .
Найти плотности распределения случайных
величин
.
Найти плотности распределения случайных
величин
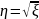 ,
,
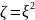 ,
,
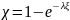 .
.
Ответ:
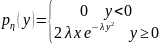 ,
,
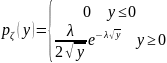 ,
,
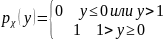 .
.
Занятия 2-3.
Многомерные законы распределения. Функции от св.
Случайным вектором
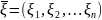 называют числовую
вектор-функцию, определенную на
называют числовую
вектор-функцию, определенную на
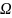 таким образом, что все множества вида
таким образом, что все множества вида
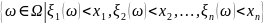 содержатся в
содержатся в
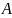 .
.
Абсолютно непрерывные
случайные вектора задаются функцией
плотности
вероятностей
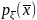 , удовлетворяющей стандартным требованиям
неотрицательности
, удовлетворяющей стандартным требованиям
неотрицательности
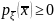 и нормированности
и нормированности
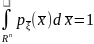 .
Вероятность принятия случайным вектором
значения во множестве
.
Вероятность принятия случайным вектором
значения во множестве
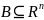 при этом полагают равной
при этом полагают равной
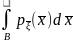 .
.
Функцией распределения
случайного вектора называется
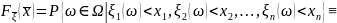
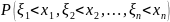 ,
где
,
где
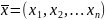 .
.
Функция
распределения случайного вектора
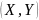 может
быть найдена с помощью плотности
распределения:
может
быть найдена с помощью плотности
распределения:
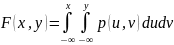 .
.
Функция
распределения обладает следующими
свойствами
(для
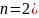 :
:
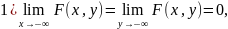
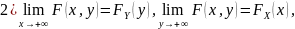
 где
где
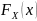 и
и
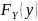 -
функции распределения составляющих
и
-
функции распределения составляющих
и
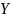 соответственно.
соответственно.
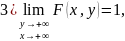 4)
4)
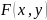 –
неубывающая функция по каждому из своих
аргументов.
–
неубывающая функция по каждому из своих
аргументов.
5) непрерывна слева по каждому из своих аргументов;
6)
Вероятность попадания случайной точки
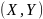 в прямоугольник со сторонами, параллельными
осям координат может быть вычислена по
формуле:
в прямоугольник со сторонами, параллельными
осям координат может быть вычислена по
формуле:
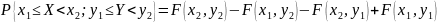 ;
;
7)
В точках непрерывности
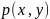 существует
существует
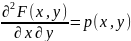 .
.
Совместный
закон распределения однозначно определяет
законы распределения компонент: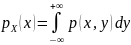 ,
,
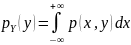 ,
,
где
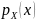 и
и
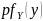 плотности распределения составляющих
и
случайного вектора;
плотности распределения составляющих
и
случайного вектора;
Математическим
ожиданием
или центром рассеивания случайного
вектора
называется неслучайный вектор
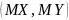 .
.
Дисперсией
случайного вектора
называется неслучайный вектор
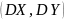 .
.
Величина
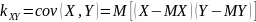 называется
ковариацией
СВ
и
.
называется
ковариацией
СВ
и
.
Ковариацию
также можно вычислить по формуле: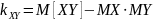 .
.
Формулы
для вычисления основных числовых
характеристик: |
|
|
Критерии независимости.
Теорема 1. Для того, чтобы СВ и были независимы, необходимо и достаточно, чтобы ФР системы была равна произведению ФР составляющих
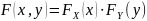 .
.
Теорема 2. Необходимым и достаточным условием независимости двух непрерывных случайных величин, образующих систему является равенство
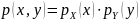 .
.
З адача
1.
Система непрерывных случайных величин
адача
1.
Система непрерывных случайных величин
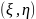 ,
равномерно распределена в области
,
равномерно распределена в области
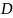 ,
ограниченной линиями
,
ограниченной линиями
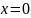 ,
,
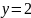 и
и
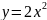 .
Найдите:
.
Найдите:
1) совместную плотность распределения ;
2) маргинальные плотности компонент и ; установить зависимость и ;
3)
коэффициент корреляции
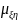 .
.
Решение. Изобразим область на координатной плоскости.
Совместная плотность системы случайных величин, равномерно распределенных в области , имеет вид
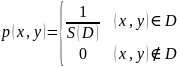 , где
, где
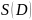 -
площадь области
-
площадь области
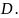 Находим ее:
Находим ее:
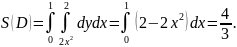
Таким
образом,
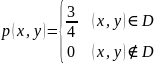 .
.
Находим маргинальные плотности:
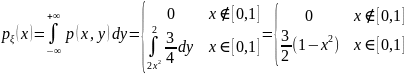 ,
,
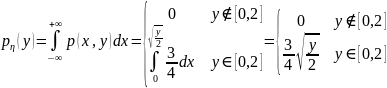 .
.
 и
приведены на рисунках.
и
приведены на рисунках.
Вычислим коэффициент корреляции:
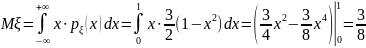 ,
,
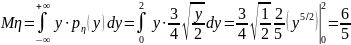 ,
,
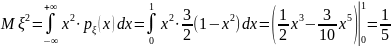 ,
,
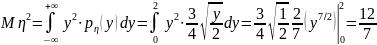 ,
,
=
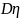 =
=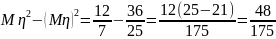 ,
,
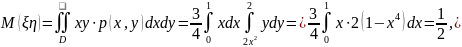
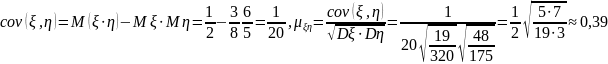 .
.
Задача
2.
Найдите законы распределения компонент
случайного вектора, равномерно
распределенного в круге радиуса
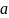 с центром в начале координат.
с центром в начале координат.
Решение. Плотность равномерно распределения в круге имеет вид:
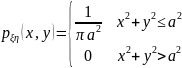 .
.
Найдем
плотности компонент:
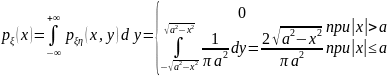 ,
,
аналогично
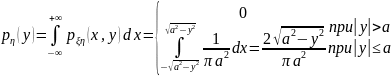 .
.
Откуда
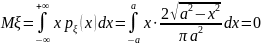 ,
а также
,
а также
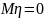 .
.
Вычислим
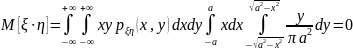 ,
следовательно,
,
следовательно,
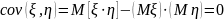 .
.
Таким
образом,
и
некоррелированы, но поскольку
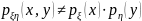 ,
то
и
зависимы.
,
то
и
зависимы.
Задача
2.
Независимые СВ
и
имеют равномерное распределение на
[0;1]. Найдите плотность распределения
случайной величины
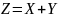 .
.
Решение. Плотности распределения вероятностей и равны
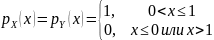 .
Пусть
.
Пусть
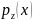 - плотность распределения суммы
- плотность распределения суммы
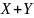 .
.
По формуле свертки получим:
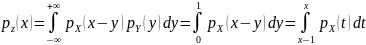
Если
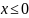 ,
то отрезок
,
то отрезок
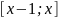 лежит левее отрезка [0;1], поэтому
лежит левее отрезка [0;1], поэтому
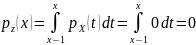 .
.
Если
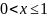 ,
то
,
то
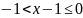 ,
поэтому
,
поэтому
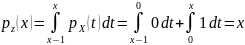 .
.
Если
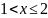 ,
то
,
то
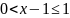 ,
поэтому
,
поэтому
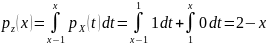 .
.
Если
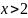 ,
то отрезок
лежит правее отрезка [0;1], поэтому
,
то отрезок
лежит правее отрезка [0;1], поэтому
.
В
итоге получаем
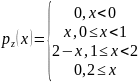 .
.
Распределение с плотностью называется треугольным распределением на отрезке [0;2] или распределением Симпсона.
Задача
3. Случайные
величины
и
независимы и одинаково распределены
по закону
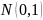 .
Найдите плотность распределения
вероятностей СВ
.
Найдите плотность распределения
вероятностей СВ
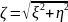 .
.
Решение. Найдем сначала совместную плотность:
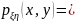
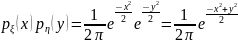 ,
так как независимы.
,
так как независимы.
Далее,
при
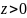 вычисляем
вычисляем
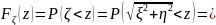
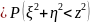 =
=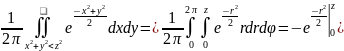 =
=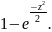
При
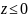
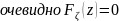 .
.
Теперь
находим
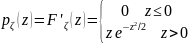 . То есть
. То есть
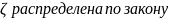 Рэлея с параметром
Рэлея с параметром
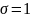 .
.
Задача
4.
В классической модели идеального газа
скорость молекулы рассматривают как
нормально распределенный случайный
вектор
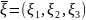 с одинаково распределенными независимыми
компонентами
с одинаково распределенными независимыми
компонентами
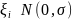 .
Найдите закон распределения абсолютной
величины скорости
.
Найдите закон распределения абсолютной
величины скорости
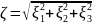 .
.
Ответ.
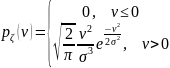 (закон
Максвелла).
(закон
Максвелла).
Задача
5. Случайный вектор
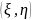 распределен по закону, определяемому
плотностью
распределен по закону, определяемому
плотностью
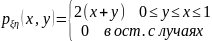 .
Найти плотности распределения случайных
величин
,
,
.
Найти плотности распределения случайных
величин
,
,
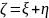 ,
,
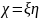 .
.
Р
 ешение.
1) Согласно общей закономерности
ешение.
1) Согласно общей закономерности
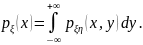 Функция
Функция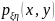 отлична от нуля только внутри треугольника,
изображенного на рисунке. Следовательно,
при
отлична от нуля только внутри треугольника,
изображенного на рисунке. Следовательно,
при
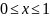
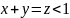
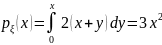 ,
а при остальных значениях
,
а при остальных значениях
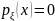 .
Получаем формулу
.
Получаем формулу
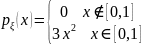 .
.
Аналогично,
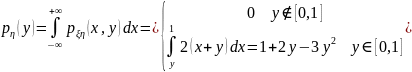 .
.
2) Вычислим функцию распределения с.в. .
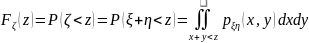 .
Из рисунка видно, что дальнейшие
вычисления зависят от значения
.
Из рисунка видно, что дальнейшие
вычисления зависят от значения
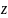 .
.
Если
,
то полуплоскость
 не имеет общих точек с треугольником,
и тогда
не имеет общих точек с треугольником,
и тогда
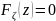 .
.
Если
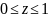 ,
то вычисление
,
то вычисление
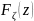 сводится к интегрированию по треугольнику,
ограниченному прямыми
сводится к интегрированию по треугольнику,
ограниченному прямыми
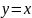 ,
,
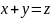 и
и
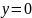 .
Получаем
.
Получаем
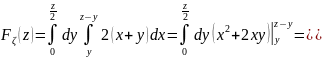
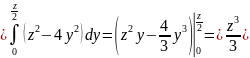 .
.
Для
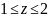 расставляем пределы по- другому:
расставляем пределы по- другому:
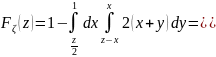
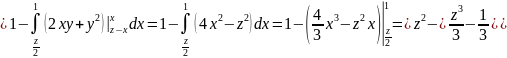 .
.
П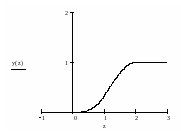 ри
ри
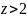
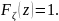 График функции приведен
на рисунке.
График функции приведен
на рисунке.
Наконец,
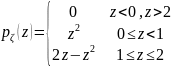 .
.
Задачи для самостоятельного решения.
1. Независимые СВ
и
имеют показательное распределение с
параметром
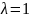 .
Найдите плотность распределения
случайной величины
.
Найдите плотность распределения
случайной величины
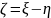 .
.
Ответ.
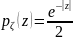 .
.
2. Независимые случайные величины и имеют равномерное распределение на [0;3]. Найдите плотность распределения СВ .
Ответ.
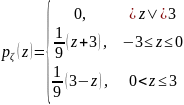 .
.
3.
Независимые СВ
и
имеют плотности распределения
соответственно
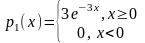 и
и
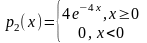 .
Найдите
.
Найдите
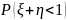 .
.
Ответ.
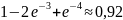 .
.
4. Независимые СВ
и
имеют показательное распределение с
параметром
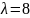 .
Найдите плотность распределения СВ
.
Найдите плотность распределения СВ
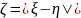 .
.
Ответ. СВ
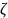 имеет показательное распределение с
параметром
.
имеет показательное распределение с
параметром
.