
- •Билет 4
- •Охарактеризуйте современную образовательную парадигму (педагогический и методический уровни).
- •Обозначьте основные проблемы реализации современной образовательной парадигмы в процессе изучения школьного курса математики.
- •Различные подходы к определению понятия функции.
- •Кубическая парабола
- •Анализ тригонометрической функции:
Различные подходы к определению понятия функции.
В методике обучения математике известны два основных направления в трактовке понятия функции: классическое (традиционное) и современное (теоретико-множественное), отражающее отдельные исторические этапы его развития. В рамках каждого направления выделяется по нескольку подходов, которые отличаются выбором определяющего (родового) понятия и соответствующей терминологии.
Анализ школьных учебников позволил определить, что используется генетическая трактовка понятия функции, но нет единого определения понятия «функции». Различные подходы к определению функции и авторы, используемые тот или иной подход в УМК, представлены на схеме:

В двух учебниках алгебры (М. И. Башмакова; Г. В. Дорофеева и др.) учащимся явно сообщается, что определение функции в математике может быть дано не единственным способом и приводятся различные трактовки термина (слова).
Несмотря на различные формулировки определений функции в них можно выделить общие моменты:
1) под термином «функция» по умолчанию подразумеваются числовые функции (они и являются объектом изучения в школе);
2) термин «переменная» используется для общего обозначения различных меняющихся величин (признак переменности функции);
3) подчеркивается одновременное наличие двух неравноправных переменных (x- независимая переменная и y- зависимая переменная);
4) четко выделен основной характерный признак функции – однозначность (в школе изучаются лишь однозначные функции);
5) речь не идет о каком-либо способе задания функции (это отдельный вопрос для изучения).
Схема исследования функции:
Функцию можно задать: графически, словесно (вербально), таблично (по значениям) и символически (аналитически, формулами).

Необходимо учитывать особенности восприятия обучающихся и рассматривать все возможные представления информации при объяснении данной темы (обозначения, геометрически, словесно, показывая примеры).
Рассмотрим схему исследования функции по М.И. Башмакову.
Способ представления |
|||
Символический |
Словесный |
Графический |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используется производная |
|
|
|
|
|
|
|
|
|
|
Четность–нечетность функции Функция называется четной, если график функции y=f(x) симметричен относительно оси ординат. Функция называется нечетной, если график функции y=f(x) симметричен относительно начала координат. |
|
|
|
Взаимо-обратные функции y=x2 Обратная
|
Обратная
функция это функция полученная из
равенства y=f(x), когда однозначно можно
выразить х через y
Геометрически: симметрия относительно прямой y=x. |
|
|
Периодические функции
|
Функция называется периодической, если существует число T>0 такое, что выполянется равенство верное при всех х. |
|
|
Точка разрыва функции – это точка около которой значение функции совершают скачок. |
Точка x0 называется точкой разрыва функции, если можно указать такое растояние d, что сколько угодно близко к х0 всегда найдутся точки, в которых значения функции расположены друг от друга на расстояни, большем чем d. |
|
|
ПРИМЕР РАЗРЫВНОЙ ФУНКЦИИ: Пусть
|
|||
Непрерывность функции на промежутке |
Функция называется непрерывной на некотором промежутке, если у нее нет на этом промежутке точек разрыва. Геометрически: след карандаша при изображение непрерывной функции. Функция называется гладкой, если в каждой точке ее графика можно однозначно провести касательную. |
|
|
Угловые точки Точки в которых нарушается гладкость. |
В угловой точке угол наклона касательной имеет скачок.
Пример:
|
|
|
Выпуклость функции |
Точка в которой меняется характер выпуклости, называется точкой перегиба функции. Если провести касательнную в точке перегиба, то на графике видно, что меняется характер выпуклости. |
|
|
Асимптота графика Вертикальные возникают если функция имеет бесконечный разрыв, скачок функции в точке разрыва бесконечен; Наклонные – если область определения бесконечна. |
Асимптота –это прямая к которой неограниченно приближается точки графика функции при их удалении от начала координат. |
|
|
Ограниченность функции Функция
может быть ограниченной сверху
|
Функция
|
Например,
функция
|
|
Представление функции в разном виде в школьном курсе математики необходимо для формирования познавательных УУД (развитие общеучебных УД: моделирование, преобразование модели с целью выявления общих законов, постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем творческого и поискового характера.), регулятивных УУД (как удобно мне), личностных УУД (что дает лично мне изучение темы функции).
Рассмотрим методическую схему Боженковой Л.И.

Пример задания: составить алгоритм изображения графиков на основе знаний алгоритмов построения графиков аналогичных степенных функций y=√x и y=∛x? Какими обладают свойствами данные функции? Какой способ изображения функции для Вас более удобен? Какие события в жизни могут описывать эти графики?




























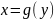 ,
где g
будет функцией, обратной к функции f.
,
где g
будет функцией, обратной к функции f.



 Эта
функция определена на всей числовой
оси, однако 0 является точкой разрыва
функции: при
Эта
функция определена на всей числовой
оси, однако 0 является точкой разрыва
функции: при



