
- •1. Предмет и задачи геодезии её связь с другими науками.
- •3 Метод проекций, принятый в геодезии. Высоты абсолютные и относитьельные. Балтийская система высот.
- •4. Географические координаты, приемущества и недостатки.
- •5. Влияние кривизны земли на горизонтальные и вертикальные расстояния.
- •6. Геодезические измерения. Единицы измерений.
- •7. Зональная система плоских прямоугольных координат (проекция Гаусса – Крюгера)
- •10.Разграфка и номенклатура топографических планов и карт.
- •11. Условные знаки планов и карт. Масштабные, внемасштабныеи пояснительные условные знаки.
- •12.Измерения площадей по картам и планам палеткой,графическим, аналитическим и механическим спсобами, точность измерений.
- •13.Полярный планиметр: устройство, измерение площадей, точность.
- •Измерение площадей планиметром
- •14. Ориентирование. Истинные (географические) азимуты, прямой и обратный азимуты, сближение мередианов. Румбы.
- •16 Магнитные азимуты и румбы, связь истинного и магнитного азимутов, склонение магнитной стрелки.
- •17. Магнитные компасы и буссоли. Устройство, применение.
- •18. Прямая и обратная геодезические задачи.
- •19. Рельеф, его изображение горизонталями, высота сечения рельефа, заложение горизонталей, свойства горизонталей, уклоны, масштаб заложений.
- •20.Основные формы рельефа и их изображение горизонталей.
- •21. Построение горизонталеей по отметкам точек. Виды интерполирования.
- •22. Виды ошибок измерений. Свойства случайных ошибок. Принцип арифметической средины.
- •23. Средняя квадратическая ошибка измерения. Формула Гаусса. Абсолютная и относительная ошибка. Предельная ошибка.
- •24. Оценка точности равноточных измерений. Ошибки функций измеренных велечин. Ошибка арифметической средней. Формула Бесселя.
- •25.Принципы организации геодезических работ. Методы построения плановых геодезических сетей(триангуляция, трилатеряция, полигонометрия).
- •26. Государственная плановая геодезическая сеть. Закрепление пунктов.
- •1 Монолит; 2 якорь; 3 пилон; 4 чугунная марка; 5 опознавательный столб;
- •1 Разрез; 2 вид торца
- •27. Государственная высотная (невеоирная) геодезическая сеть. Закрепление пунктов.
- •28. Сети сгущения (местные сети) плановые и высотные.
- •Плановые геодезические сети сгущения
- •Высотные (нивелирные) сети сгущения
- •29. Съёмочные сети. Теодолитные ходы. Закрепление точек.
- •Плановые съемочные сети
- •Высотные съемочные сети
- •30. Измерение длины линий. Дальномеры, мерные ленты и рулетки. Точность измерений.
- •31.Поправки вводимые при измерении длин. За компарирование, температуру, наклон.
- •32. Подготовка теодалита к работе (центрирование, невелирование, подготовка зрительной трубы).
- •33. Основные узлы теодолита: отсчетные устройства, уровни, зрительные трубы, их характеристики . Эксцентриситет алидады.
- •34. Классификация тедолитов. Поверки теодолитов.
- •3. Поверка положения горизонтальной оси теодолита.
- •4. Поверка сетки нитей.
- •35. Измерение горизонтального угла (способ приёмов)
- •36. Вертикальный круг теодолита. Измерение вертикальных углов. Формулы, используемые при обработке результатов.
- •37. Теодолитная съёмка. Состав работ. Полевые работы. Съёмка подробностей.
- •39.Нивелирование. Способы нивелирования: геометрический, тригонометрический, физический.
- •40. Геометрическое невелирование. Нивелирование из середины и вперёд, простое и сложное, продольно и поперечное.
- •42. Поверки нивелиров. Влияние рефракции и кривизны Земли на точность геометрического нивелирования.
- •43. Нивелирование трассы. Полевые работы. Разбивка пикетов, их закрепление.
- •44. Элементы закругления. Разбивка главных точек. Детальная разбивка.
- •45. Камеральные работы при нивелирование трассы. Построение профиля.
- •46. Нивелирование поверхности. Нивелирование по квадратам. Составление картограммы земляных работ.
- •47. Тригонометрическое нивелирование. Тахеометрические формулы.
- •48. Устройство и принцип действия оптических дальномеров. Нитяной дальномер.
- •49. Тахеометрическая съёмка. Применяемы приборы. Полевые работы.
- •50. Камреальные работы при тахеомитрической съёмки. Составление плана.
- •3.Построение линии проектной длины в заданном направлении
- •53.Вынос в натуру проектной отметки, проектного горизонтального угла, длины линии, линии и плоскости заданного уклона.
- •54. Закрепление точек и осей сооружения на местности. Обноска, створные знаки. Использование их при монтаже конструкции.
- •55. Наблюдение за деформациями сооружений. Методы определения сдвига, осадка и крена сооружения.
- •56. Исполнительные съемки.
- •57. Цифровые и математические модели местности.
- •58. Перспективы развития современного геодезического оборудования.
- •59. Спутниковые геодезические системы. Методика их применения в современных условиях.
4. Географические координаты, приемущества и недостатки.
В системе географических координат местоположение проекции точки на сфероиде определяется двумя углами: широтой и долготой (рис. 34).

Рис. 34
Широтой точки называют угол, образованный отвесной линией в данной точке и плоскостью экватора. Этот угол отсчитывается от плоскости экватора на север и на юг, изменяясь от 0 до 90°. Соответственно широта бывает северная (+) и южная (–).
Долготой точки называют двугранный угол, заключенный между плоскостью начального (Гринвичского) меридиана, и плоскостью меридиана, проходящего через данную точку. От начального меридиана долготу отсчитывают на восток и запад, от 0 до 180°. Соответственно долгота бывает восточная (+) и западная (–).
Для непосредственного определения географических координат точки на карте используют линии меридианов и параллелей. Меридиан – линия пересечения уровенной поверхности плоскостями, проходящими через ось вращения Земли, т.е. плоскостями долгот.
Параллель – линия пересечения уровенной поверхности плоскостями, перпендикулярными оси вращения Земли, т.е. плоскостями широт.
Система географических координат удобна для изучения всей физической поверхности Земли или значительных ее участков, но неудобна для решения многих инженерных задач.
Географические координаты характеризуються тем, что линейные велечины, соответствующие еденицы угловой велечины по параллелям и мередианам, будут различны и зависят от положения линии на земной поверхности. Для решения геодезических задач этосоздаёт большие трудности и приводит к сложным пересчётам.
Используются в случаях, когда нет необходимости учитывать разницу между названными координатами. Астрономические широту и долготу определяют с помощью специальных приборов относительно уровенной поверхности и направления силы тяжести. При проецировании астрономических координат на поверхность земного референц-эллипсоида получают геодезические широту и долготу.
5. Влияние кривизны земли на горизонтальные и вертикальные расстояния.
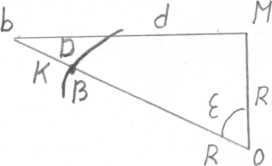
При замене небольшого участка BD (рис. 13) уровенной поверхности Земли касательной BD1 (см. §6 и рис. 9) точка D перемещается в D', в связи с чем меняется ее высота на величину р. Величина р выражает влияние кривизны Земли на высоты точек и назывется поэтому поправкой за кривизну Земли. Определим ее величину.

Влияние кривизны земли при измерении расстояний и высот.
Получить ортогональную проекцию на ортогональной плоскости наиболее просто поскольку нельзя учитывать кривизну земли.
![]() при R=6000
км d=10км
при R=6000
км d=10км
![]() -
относительная поверхность
-
относительная поверхность
20*20км2 – считаются плоскими
k – величина отражающая влияние кривизны земли на точность определения высот точек земной поверности
![]()
d(м) 100 300 500 1000
к(см) 0,1 0,8 2,3 8,1
6. Геодезические измерения. Единицы измерений.
Под измерениями понимают процесс сравнения какой-либо величины с другой однородной величиной, принимаемой за единицу. При всем многообразии геодезических измерений все они сводятся в основном к трем видам:
линейные — определяются расстояния между заданными точками;
угловые — определяются значения горизонтальных и вертикальных углов между направлениями на заданные точки;
высотные (нивелирование) — определяются разности высот отдельных точек.
За единицу линейных и высотных измерений (расстояний, высот и превышений) в геодезии принят метр, представляющий собой длину жезла - эталона, изготовленного из платино-иридиевого сплава в 1889 г. и хранящегося в Международном бюро мер и весов в Париже. Копия №28 этого жезла находится в НИИ метрологии им. Д. И. Менделеева в Санкт-Петербурге. В качестве эталона более высокой точности в настоящее время служит метр, определенный как длина пути, пройденного светом за 1/299792548 доли секунды.
Единицей для измерений углов (горизонтальных и вертикальных) служит градус, представляющий 1/90 прямого угла или 1/360 окружности. Градус содержит 60 угл. мин, минута делится на 60 угл. с. В некоторых странах применяют градовую систему, в которой 1 град составляет 1/400 окружности, градовая минута — 1/100 град, а градовая секунда — 1/100 град мин.
В современных автоматизированных угломерных приборах единицей измерений служит гон, равный 1 град или 54 угл. мин; тысячная его доля, равная 3,24 угл. с, называется миллигон.
Измерения называют прямыми, если их выполняют с помощью приборов, позволяющих непосредственно сравнить измеряемую величину с величиной, принятой за единицу, и косвенными, когда искомую величину получают путем вычислений на основе результатов прямых измерений. Так, угол в треугольнике можно не посредственно измерить угломерным прибором (прямое измерение) или вычислить по результатам измерения трех сторон треугольника (косвенное измерение).
Необходимыми условиями любого измерения являются: объект измерения; субъект измерения — лицо, производящее измерение; мерный прибор, которым выполняют измерения; метод измерения — совокупность правил и действий, определяющих процесс измерения; внешняя среда, в которой выполняют измерения.
Обозначенные на местности точки, от которых выполняют геодезические измерения, называются исходными. Точки, положение которых на местности необходимо определить, называют определяемыми.
Исходные и определяемые точки могут располагаться в горизонтальной плоскости в плане (плановые точки) и вертикаль ной — по высоте (высотные точки).
Измерение - процесс сравнения физической величины с единицей меры, другой однородной величиной. В инженерной геодезии за единицы измерений приняты метр, градус, минута, радиан.
Один метр - длина пути, проходящего электромагнитной волной в вакууме за 1/С долю секунды, где С = 299792458.
Один градус - 1/90 часть прямого угла (1 = 60', 1'= 60"). Центральный угол, опирающийся на дугу окружности равную радиусу называется радианом (1 рад.= 57.3 = 3438'= 206265").
Измерения различают равноточные и неравноточные. Равноточные – это результаты измерений однородных величин, выполняемые с помощью приборов одного класса, одним и тем же методом, одним исполнителем при одних и тех же условиях. Все остальные измерения относятся к неравноточным.
