
Примеры / Primer_Tr_2_matanaliz
.docxПример решения типового расчета № 2
«Математический анализ»
Задание №1
Дано
комплексное число
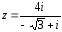 .
.
-
Записать число
 в алгебраической, тригонометрической
и показательной форме, изобразив его
на комплексной плоскости.
в алгебраической, тригонометрической
и показательной форме, изобразив его
на комплексной плоскости. -
Вычислить
 .
.
Решение:
1.
Приведем
 к алгебраической форме комплексного
числа. Для этого умножим числитель и
знаменатель дроби на число
к алгебраической форме комплексного
числа. Для этого умножим числитель и
знаменатель дроби на число
 комплексно сопряженное знаменателю.
Получим:
комплексно сопряженное знаменателю.
Получим:

Итак,
 алгебраическая
форма комплексного числа
алгебраическая
форма комплексного числа
 .
.
Запишем
Имеем:
 в тригонометрическом виде, используя
формулу (1):
в тригонометрическом виде, используя
формулу (1):
 ,
,

 на комплексной плоскости:
на комплексной плоскости:

0
1 х
у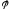







Итак, тригонометрическая форма имеет вид:
 .
В показательной форме:
.
В показательной форме:
 .
.
2.
Вычислим
 ,
используя формулу:
,
используя формулу:

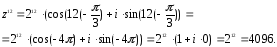
Ответ:
1.
 ;
;
2.

Пример 2.
-
Решить уравнение
 .
. -
Записать корни уравнения
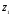 и
и
 в алгебраической, тригонометрической
и показательной форме, изобразив их на
комплексной плоскости.
в алгебраической, тригонометрической
и показательной форме, изобразив их на
комплексной плоскости.
Решение:
-
Найдем корни данного квадратного уравнения по известной формуле
 ,
зная, что
,
зная, что
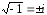 .
.
(Знак
 используется
как квадратный корень из комплексного
числа!)
используется
как квадратный корень из комплексного
числа!)
Получим два комплексно сопряженных корня
 .
.
2.
Имеем алгебраическую форму
 и
и
 .
.
Действительная и мнимая часть, соответственно, равны:

Изобразим
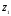 и
и
 на
комплексной плоскости:
на
комплексной плоскости:
y Запишем
числа
Имеем:

 и
и
 в тригонометрической и показательной
форме.
в тригонометрической и показательной
форме. ,
,

 ,
, ;
;


 ,
,

 ;
;
 ;
;

 .
.
Ответ:


Задание № 2
Вычислить пределы.
Решение.
 1.
1. (разложим
числитель и знаменатель на множители)
(разложим
числитель и знаменатель на множители) ;
;
2.
 (разделим
числитель и знаменатель на наибольшую
степень
(разделим
числитель и знаменатель на наибольшую
степень
 ;
в данном случае на
;
в данном случае на
 )=
)=
 (т.к.
функция, обратная бесконечно большой,
есть бесконечно малая:
(т.к.
функция, обратная бесконечно большой,
есть бесконечно малая:
 );
);
3.
 (умножим числитель и знаменатель на
(умножим числитель и знаменатель на
 )
)
=


 ;
;
4.
 (применим
правило Лопиталя (3))
(применим
правило Лопиталя (3))
 .
.
Ответ:
1.
 ; 2.
; 2.
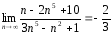 ;
;
3.
 ;
4.
;
4.

Задание №3
Подобрать
параметры
 и
и
 так, чтобы функция
так, чтобы функция
 была
непрерывна.
была
непрерывна.
Решение.

Функция
 составлена из элементарных функций,
каждая из которых непрерывна на указанных
промежутках. Непрерывность может
нарушаться только в точках
составлена из элементарных функций,
каждая из которых непрерывна на указанных
промежутках. Непрерывность может
нарушаться только в точках
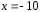 и
и
 .
.
Вычислим
односторонние пределы функции
 в
этих точках.
в
этих точках.
а)
 ;
;
 ;
;
 .
.
Условие
непрерывности функции в точке
 записывается в виде
записывается в виде
 .
.
б)
 ;
;
 ;
;
 .
.
Условие
непрерывности функции в точке
 записывается в виде
записывается в виде
 .
.
в) Получаем систему линейных уравнений:
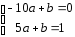 .
.
Решение
системы дает значения искомых параметров:
 .
.
Ответ:

Задание №4
Продифференцировать
данные функции по переменной
 .
.
1.
 ;
2.
;
2.
 ;
3.
;
3.
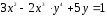 .
.
Решение.
1.
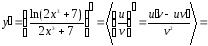
 .
.
Используем
правило дифференцирования сложной
функции: если
 ,
где функции
,
где функции
 и
и
 имеют производные, то
имеют производные, то
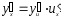 .
Полагаем
.
Полагаем
 и
и
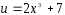 .
Получаем:
.
Получаем:
 .
.
Тогда

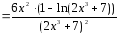 .
.
2. В этой задаче функция задана параметрически, т.е. уравнениями:
 .
.
Производная
 находится по формуле:
находится по формуле: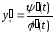 .
.
Проводим вычисления:
 ;
;
 .
.
3.
Функция задана неявно уравнением
 .
Для определения
.
Для определения
 нужно продифференцировать функцию
нужно продифференцировать функцию
 по
по
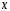 ,
рассматривая при этом
,
рассматривая при этом
 как функцию переменной
как функцию переменной
 .
Приравнивая полученную производную к
нулю, получаем уравнение первой степени
относительно
.
Приравнивая полученную производную к
нулю, получаем уравнение первой степени
относительно
 .
Из этого уравнения и находим производную.
.
Из этого уравнения и находим производную.
 ,
,
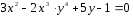 ,
,
 ,
,
 ,
,

 .
.
Ответ:
1.
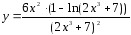 ;
;
2.
 ;
3.
;
3.
 .
.
Задание №5
Исследовать функцию с помощью производной и построить график.

Решение.
1.
Область определения функции:
 ;
;
 ;
;

2. Точки пересечения с осями координат.
 ,
так как уравнение
,
так как уравнение
 не имеет вещественных корней, то график
функции не имеет точек пересечения с
осью
не имеет вещественных корней, то график
функции не имеет точек пересечения с
осью
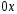 .
.
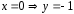 ,
т.е. график пересекает ось
,
т.е. график пересекает ось
 в точке (0;–1).
в точке (0;–1).
3. Исследование функции на четность (нечетность).
 .
.
Функция не является ни четной, ни нечетной, т.е. – это функция общего вида.
4. Функция непериодическая.
5. Исследование непрерывности. Классификация точек разрыва.
Функция
терпит разрыв в точке
 .
Определим тип разрыва:
.
Определим тип разрыва:
 .
.
Односторонние
пределы функции бесконечны, следовательно,
 –
точка разрыва второго рода (точка
бесконечного разрыва).
–
точка разрыва второго рода (точка
бесконечного разрыва).
6. Интервалы монотонности, точки экстремума функции.
Найдем первую производную функции:



 ,
,
 .
.

Точки экстремума:
Функция
имеет максимум при
 ,
так как в при переходе через эту точку
производная меняет знак с (+) на (–),
причем
,
так как в при переходе через эту точку
производная меняет знак с (+) на (–),
причем
 .
.
Функция
имеет минимум при
 ,
так как при переходе через эту точку
производная меняет знак с (–) на (+),
причем
,
так как при переходе через эту точку
производная меняет знак с (–) на (+),
причем
 .
.
Функция
возрастает при
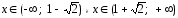 .
.
Функция
убывает при

7. Интервалы выпуклости и точки перегиба.
Найдем вторую производную функции:

 в
ноль не обращается, значит, точек перегиба
нет.
в
ноль не обращается, значит, точек перегиба
нет.

При
 направление выпуклости графика вверх
(выпуклость), а при
направление выпуклости графика вверх
(выпуклость), а при
 – вниз (вогнутость).
– вниз (вогнутость).
8. Асимптоты.
Прямая
 является вертикальной асимптотой
графика функции (см. пункт 5).
является вертикальной асимптотой
графика функции (см. пункт 5).
Найдем
наклонные асимптоты
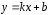 :
:
 ;
;

Итак,
график имеет наклонную асимптоту
 (правую
и левую).
(правую
и левую).
9. График функции.

-1
 0
1
0
1
 x
x
