
- •Министерство образования и науки Украины
- •Кафедра высшей и прикладной математики
- •Методические рекомендации
- •Содержание
- •Введение
- •І. Введение в анализ
- •Понятие предела функции, свойства
- •Раскрытие некоторых видов неопределенностей
- •Іі. Дифференциальное исчисление функций одной переменной
- •Понятие производной, ее свойства
- •Производные высших порядков
- •Дифференцирование некоторых функций
- •2.4. Применение дифференциального исчисления к исследованию функций одной переменной
- •Ііі. Интегральное исчисление
- •3.1. Понятие неопределеннного интеграла, свойства
- •Свойства неопределенного интеграла
- •3.2. Определенный интеграл. Основные свойства
- •3.3. Основные методы интегрирования
- •Интегрирование тригонометрических выражений
- •Іv. Дифференциальные уравнения
- •4.1. Основные понятия
- •4.2. Дифференциальные уравнения первого порядка
- •4.3. Дифференциальные уравнения второго порядка с постоянными коэффициентами
- •V. Числовые ряды
- •5.1. Основные понятия
- •Необходимый признак сходимости ряда Если ряд сходится, то его -й член стремится к нулю при неограниченном возрастании , т.Е.
- •5.2. Достаточные признаки сходимости
- •Знакочередующиеся ряды. Признак Лейбница
- •5.3. Степенные ряды. ИНтервал сходимости
- •Контрольная работа
- •Литература
3.3. Основные методы интегрирования
Основными методами интегрирования являются непосредственное интегрирование при помощи основных свойств неопределенного и определенного интеграла и таблицы интегралов, метод подстановки (замены переменной) и интегрирование по частям.
Метод непосредственного интегрирования
Метод состоит в том, что с помощью алгебраических преобразований подынтегральная функция приводится к табличной или их сумме. Рассмотрим этот метод на примерах.
Примеры:

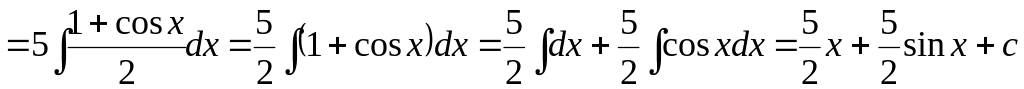 .
.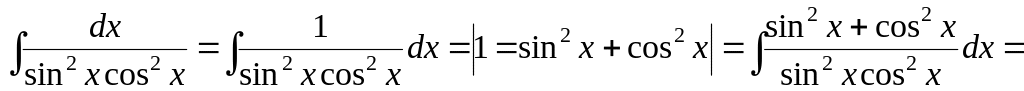
![]() .
.
Метод подстановки
Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла или интеграла, берущегося тем или иным известным приемом. Такой метод называется методом подстановки, а также методом замены переменной.
Рассмотрим
функцию
,
где![]() ,
тогда:
,
тогда:
![]() (3.1)
(3.1)
Формула (3.1) называется формулой замены переменной в неопределенном интеграле.
После
нахождения интеграла
![]() надо вместо
надо вместо
![]() подставить его выражение через
.
В определенном интеграле возврат к
переменной
не обязателен, но в этом случае при
замене переменной необходимо изменить
пределы интегрирования, т. е. воспользоваться
формулой:
подставить его выражение через
.
В определенном интеграле возврат к
переменной
не обязателен, но в этом случае при
замене переменной необходимо изменить
пределы интегрирования, т. е. воспользоваться
формулой:
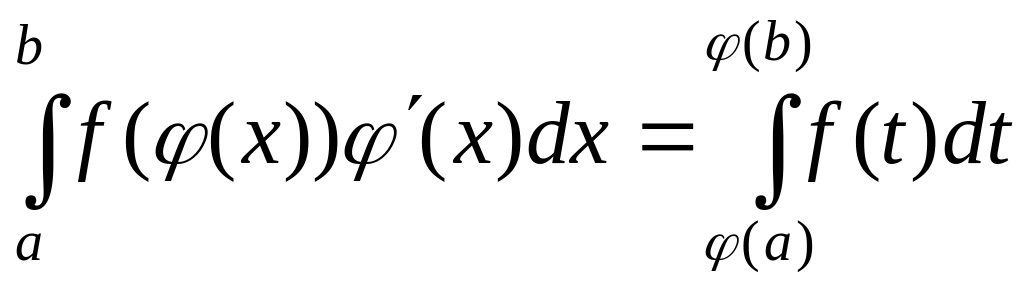 .
.
Примеры.
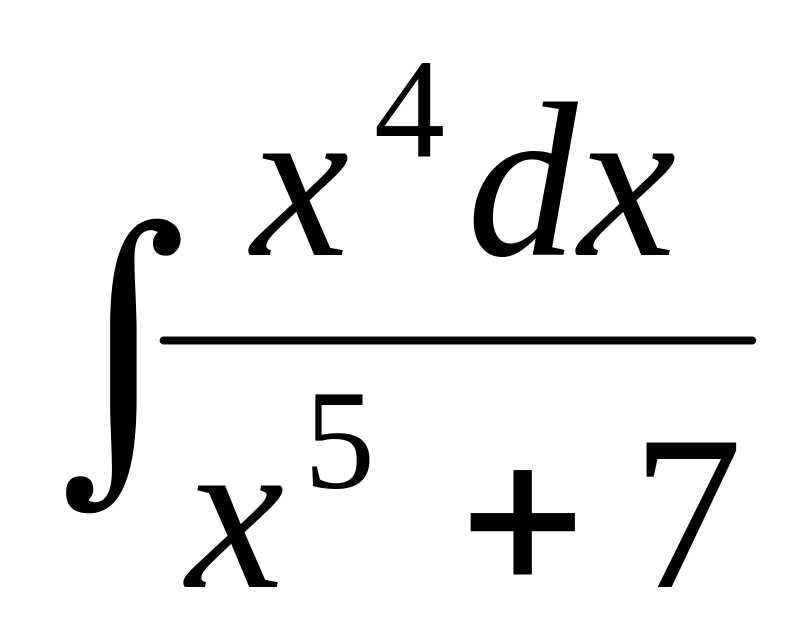 .
.
Обозначим
![]() ,
тогда
,
тогда
![]() и, следовательно,
и, следовательно,
![]() .
.
![]() .
.
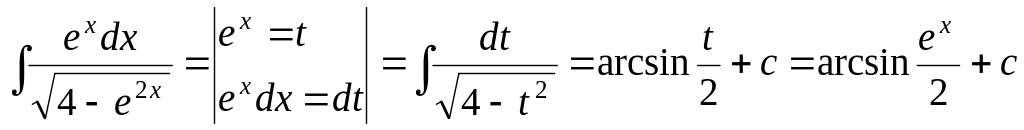 .
.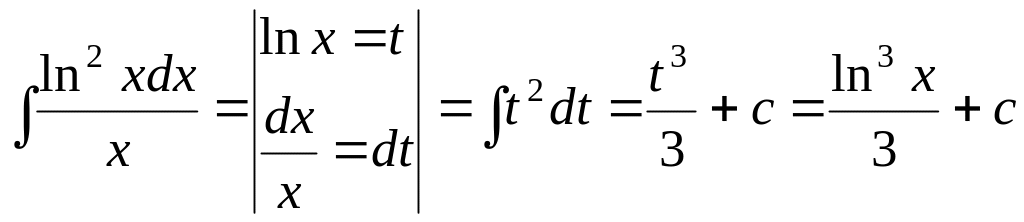 .
.
|
Полагаем
|
|
|
|
значения
|
1
при
значения
определяем
1
2
я
соотношени
из
этого
Для
интеграла.
пределы
новые
теперь
Находим
.
2
откуда
,
2
находим
е,
соотношени
это
руя
Дифференци
.
1
2
полагаем
1
1
x
z
z
x
dz
dx
dz
dx
z
x![]()
В приведенных выше примерах метод замены переменной быстро привел к цели. Однако удачный выбор новой переменной обычно представляет известные трудности. Для их успешного преодоления необходимо хорошо владеть техникой дифференцирования, уметь «прикидывать», что даст та или иная подстановка, и твердо знать табличные интегралы.
Интегрирование по частям
Пусть
функции
![]() и
и
![]() непрерывно дифференцируемы на некотором
промежутке, тогда:
непрерывно дифференцируемы на некотором
промежутке, тогда:
![]() .
(3.2)
.
(3.2)
Формулу (3.2) обычно записывают в виде:
![]() .
(3.2*)
.
(3.2*)
Для определенного интеграла она такова:
![]() .
.
Эти
формулы называются формулами интегрирования
по частям. Правильнее было бы назвать
их формулами частичного интегрирования.
При известных
и
![]() они сводят нахождение интеграла от
они сводят нахождение интеграла от
![]() после частичного интегрирования к
нахождению интеграла от
после частичного интегрирования к
нахождению интеграла от
![]() .
Иногда удается функции
и
выбрать так, что новый интеграл либо
сам является табличным, либо сводится
к табличным интегралам уже известными
методами.
.
Иногда удается функции
и
выбрать так, что новый интеграл либо
сам является табличным, либо сводится
к табличным интегралам уже известными
методами.
При
этом следует учитывать, что за
принимается функция, которая
дифференцированием упрощается, а за
![]() - та часть подынтегрального выражения,
содержащая
- та часть подынтегрального выражения,
содержащая
![]() ,
интеграл от которой известен или может
быть найден.
,
интеграл от которой известен или может
быть найден.
Так,
при вычислении интегралов вида
![]() ,
,
![]() ,
,
![]() за
следует принять многочлен
за
следует принять многочлен
![]() ,
а за
- соответственно выражения -
,
а за
- соответственно выражения -
![]() ,
,
![]() ,
,
![]() .
.
При
вычислении интегралов вида
![]() ,
,
![]() ,
,
![]() за
следует принять выражение
за
следует принять выражение
![]() ,
а за
- соответственно функции
,
а за
- соответственно функции
![]() ,
,
![]() ,
,
![]() .
.
Примеры.
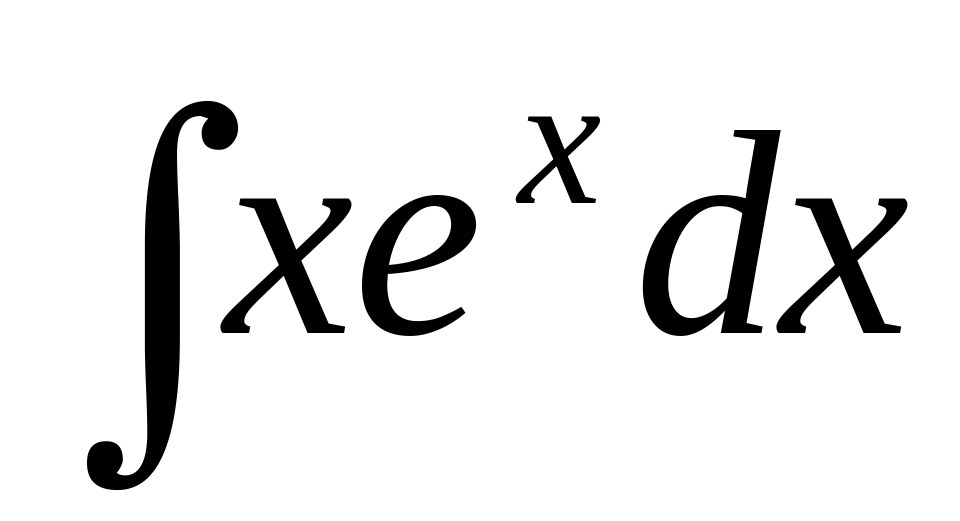 .
Полагаем
.
Полагаем
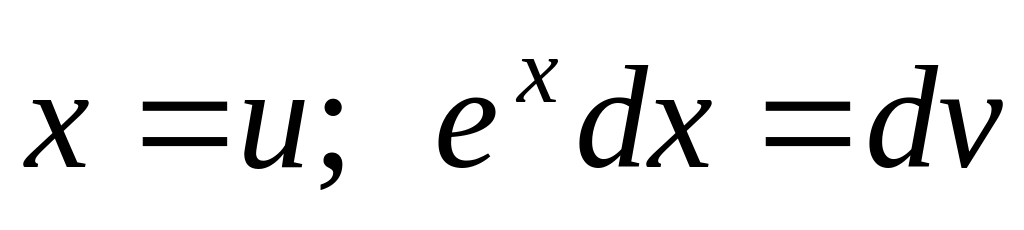 .
Тогда
.
Тогда
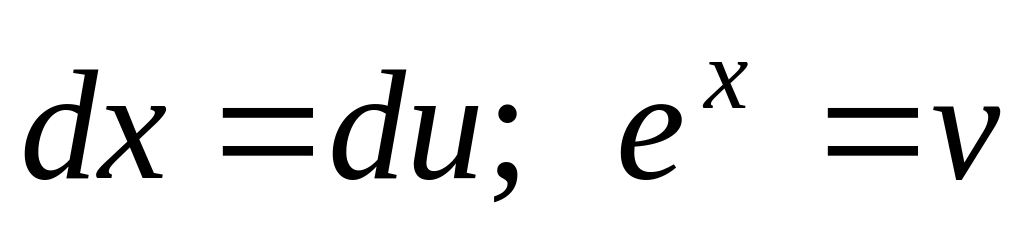 и, значит, по формуле (3.2*).
и, значит, по формуле (3.2*).
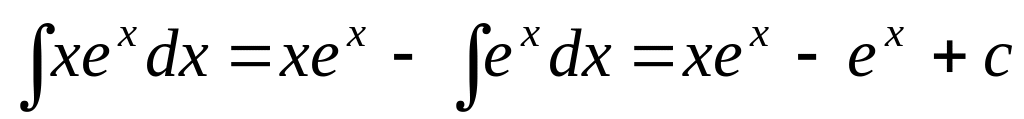 .
.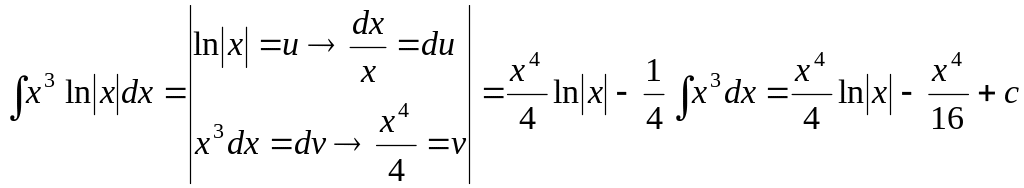 .
.
3.
![]()
![]()
![]()
Формулу интегрирования по частям применили дважды.
4.
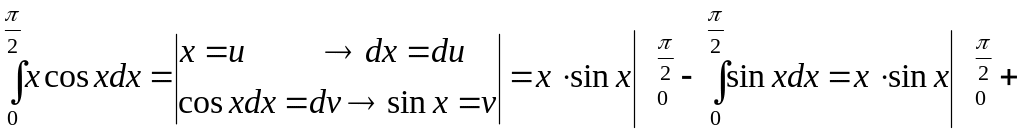
![]() .
.
Интегрирование рациональных функций
Рациональной
функцией называется дробь вида
![]() ,
где
и
,
где
и
![]() - целые многочлены.
- целые многочлены.
Рациональная дробь называется правильной, если степень ниже степени , в противном случае дробь называется неправильной.
Если дробь неправильная, то путем почленного деления числителя на знаменатель по правилу деления многочленов следует выделить целую часть и правильную дробь. Поэтому будем рассматривать интегрирование правильных дробей, поскольку интегрирование целой части не вызывает затруднений.
Метод неопределенных коэффициентов.
Так как интегрирование многочлена не представляет трудностей, то достаточно научиться интегрировать правильные рациональные дроби. Сформулированная ниже теорема позволяет свести интегрирование любой правильной рациональной дроби к интегрированию элементарных дробей.
Теорема.
Если
![]() - правильная рациональная дробь,
знаменатель
которой представлен в виде произведения
линейных и квадратичных множителей (с
действительными коэффициентами):
- правильная рациональная дробь,
знаменатель
которой представлен в виде произведения
линейных и квадратичных множителей (с
действительными коэффициентами):
![]() (3.3)
(3.3)
то эта дробь может быть разложена на элементарные дроби по следующей схеме:
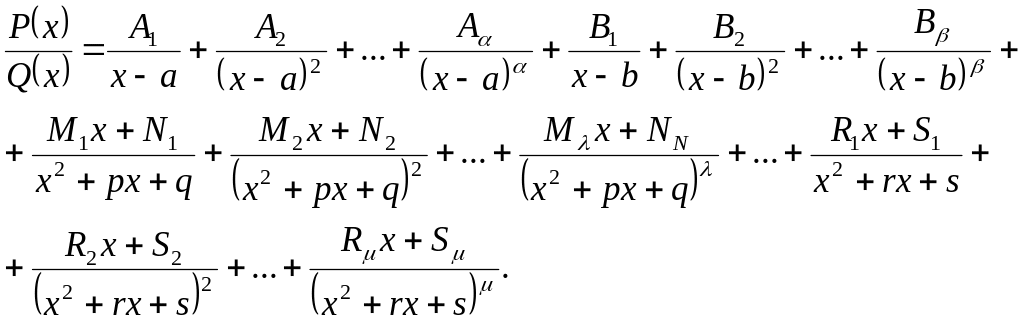 (3.4)
(3.4)
где
![]() - некоторые действительные числа.
- некоторые действительные числа.
Практически разложение конкретной правильной рациональной дроби на сумму элементарных дробей обычно производят методом неопределенных коэффициентов. Для этого:
разлагают знаменатель на произведение линейных и квадратичных множителей;
записывают разложение дроби по схеме (3.4) с неопределенными коэффициентами;
приводят элементарные дроби к общему знаменателю ;
приравнивают многочлен, получившийся в числителе, к многочлену .
Для того чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы коэффициенты при одинаковых степенях у них были равны. Учитывая это замечание, приравниваем коэффициенты при одинаковых степенях в левой и правой частях равенства, получая тем самым систему алгебраических уравнений для нахождения неопределенных коэффициентов.
Существование такой системы вытекает из сформулированной выше теоремы.
Примеры.
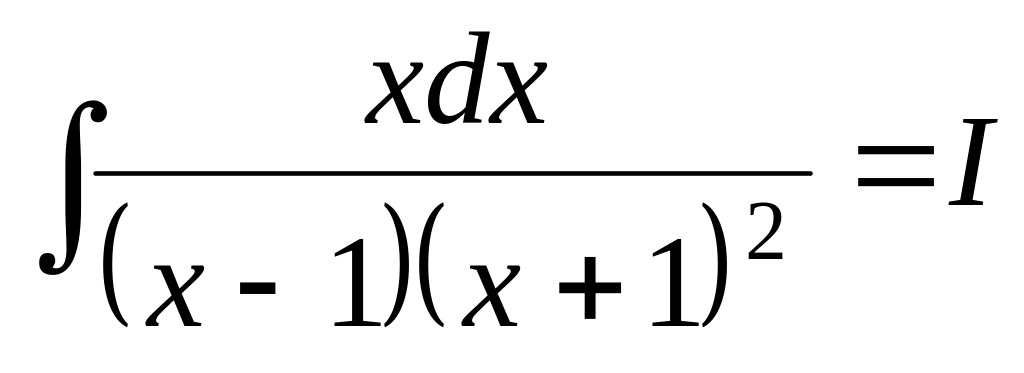 .
.
Решение.
Имеем:
![]() .
.
Отсюда:
![]() .
(*)
.
(*)
а) Первый способ определения коэффициентов.
Перепишем тождество (*) в виде:
![]() .
.
Приравнивая коэффициенты при одинаковых степенях , получим:
![]() .
.
Отсюда:
![]() ;
;
![]() ;
;
![]() .
.
б) Второй способ определения коэффициентов.
Полагая
в тождестве (*), будем иметь:
![]() ,
т.е.
.
,
т.е.
.
Полагая
![]() ,
получим:
,
получим:
![]() ,
т.е.
.
,
т.е.
.
Далее, полагая
![]() ,
будем иметь:
,
будем иметь:
![]() ,
т.е.
.
,
т.е.
.
Следовательно:
![]()
![]() .
.
2. Найти:
![]() .
.
Решение.
Имеем:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
т.е.
,
т.е.
![]() .
.
Таким образом:
![]() ,
и
,
и
![]() .
.
Следовательно:
![]()
![]() .
.
