Понятие предела функции, свойства
Пусть
функция
задана на интервале
.
Определение: |
Число
|
называется пределом функции
в точке
,
если для любого
существует
такое, что при всех
,
удовлетворяющих условию
выполнено:
.
Определение: |
Число
называется правосторонним (левосторонним)
пределом функции
в точке
,
если для любого числа
|
существует
такое, что для любого
выполнено:
.
Обозначение:
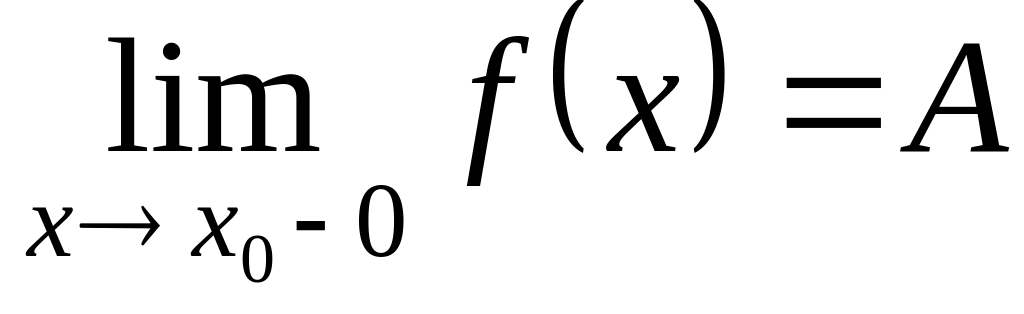(для левостороннего предела);
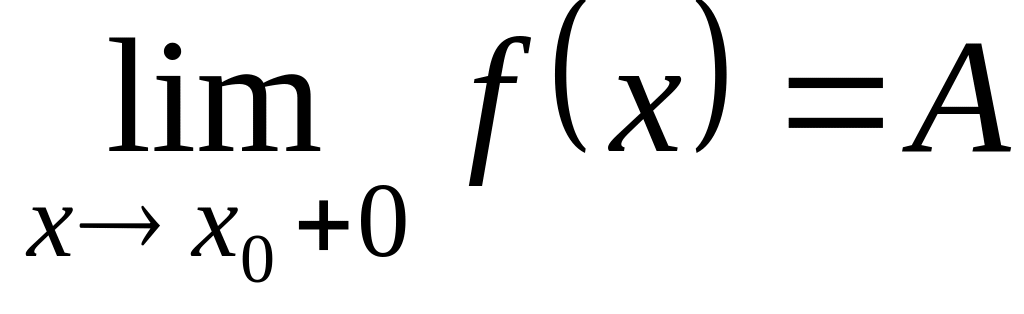(для правостороннего предела).
Практическое вычисление пределов основано на следующих теоремах:
Функция имеет в точке предел тогда и только тогда, когда в этой точке существуют правосторонний и левосторонний пределы и они равны. В этом случае предел функции равен односторонним пределам.
Арифметические действия над пределами:
Если
и
,
то справедливы утверждения:
;
;
,
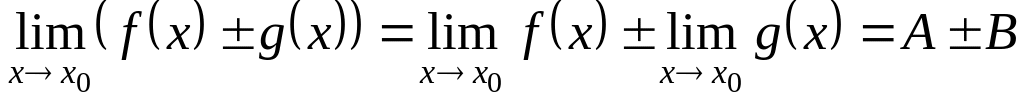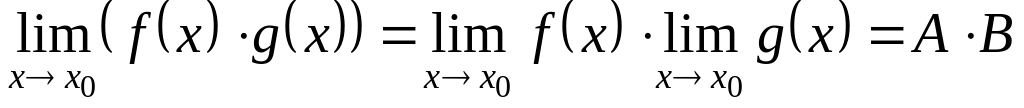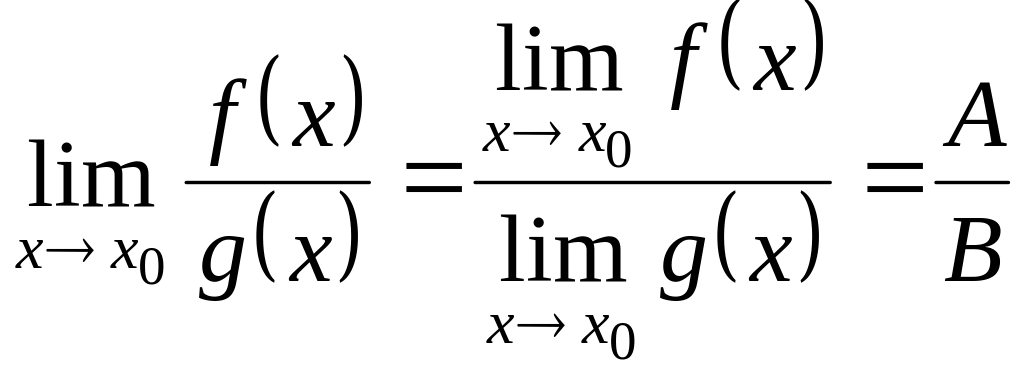при условии, что
.
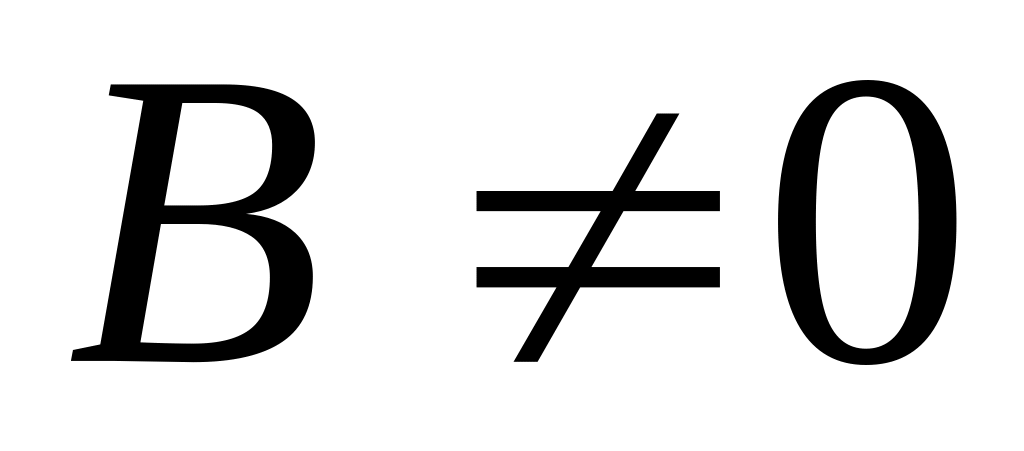Первый замечательный предел:
.
(1.1)
Второй замечательный предел:
или
.
(1.2)
Раскрытие некоторых видов неопределенностей
Начинать нахождение предела надо с подстановки в функцию предельного значения аргумента. При этом можем получить неопределенности вида:
.
Неопределенность вида
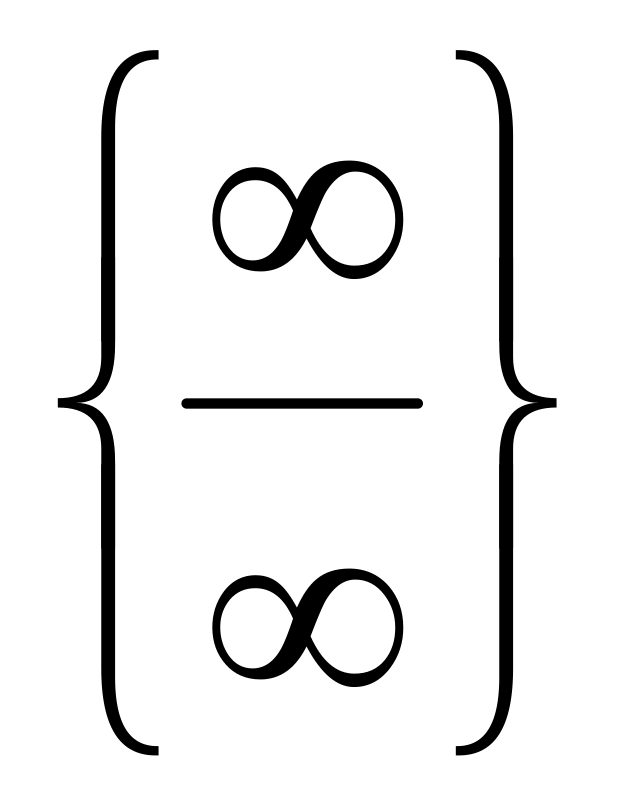(в числителе и знаменателе –
многочлены).
Примеры такого вида решаются путем почленного деления числителя и знаменателя на старшую степень переменной, при этом:
а) если старшая степень числителя равна старшей степени знаменателя, то предел равен отношению коэффициентов при старших степенях.
Пример № 1.
,
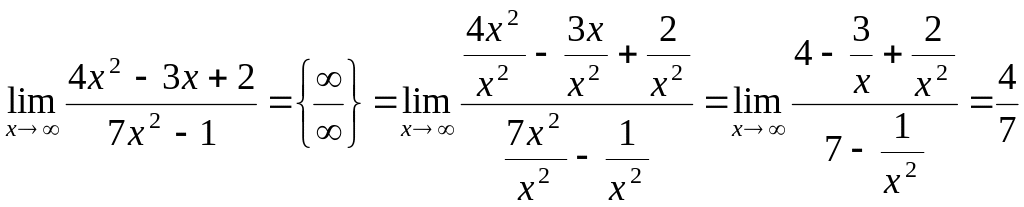(т.к. при
)
б) если старшая степень числителя больше старшей степени знаменателя, то предел равен бесконечности:
Пример № 2.
,
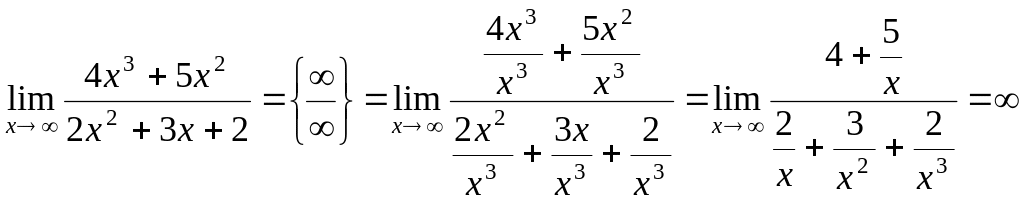(т.к. в пределе получили отношение конечного к бесконечно малому).
в) если старшая степень числителя меньше старшей степени знаменателя, то предел равен нулю:
Пример № 3.
.
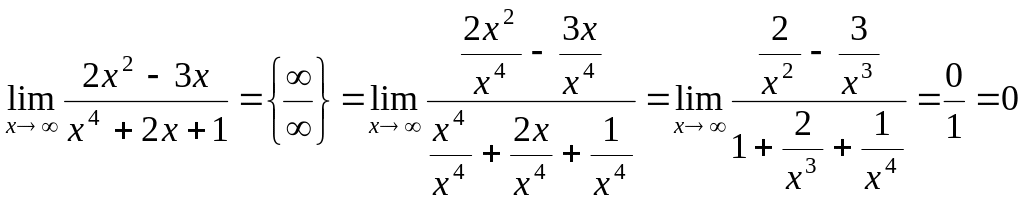Неопределенность вида
.
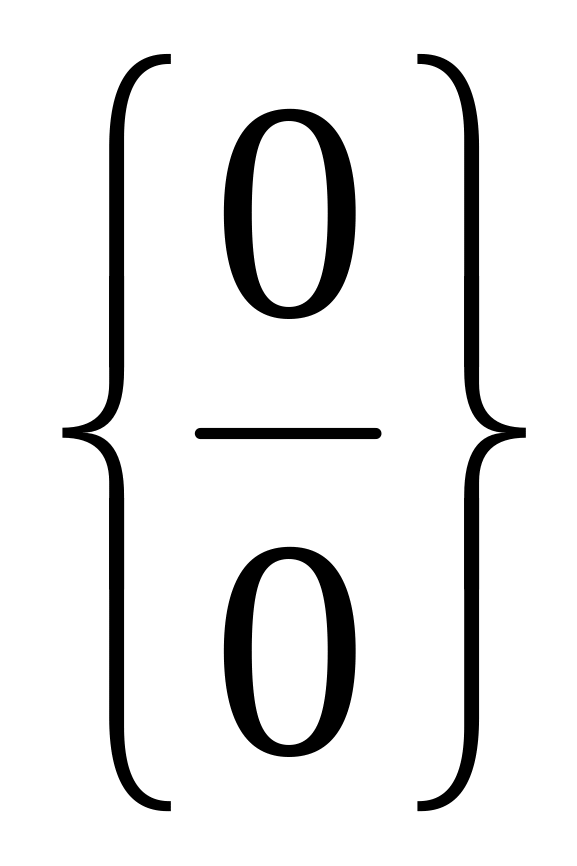а) В числителе и знаменателе – многочлены. Надо разложить числитель и знаменатель на множители, с целью выделения критического множителя, т.е. множителя, который порождает неопределенность.
Пример № 4.
.
б) Выражение содержит иррациональность в числителе или знаменателе дроби (или и в числителе и в знаменателе).
Примеры такого вида решаются путем домножения числителя и знаменателя на выражение, сопряженное числителю (знаменателю или и числителю и знаменателю одновременно).
Пример № 5.
;
Пример № 6.
.
Пример № 7.
Вычислить:
.
Решение.
Вычислим, используя
первый замечательный предел
.
Пусть
,
тогда
.
Если
,
то
.
Используя эту замену, имеем:
.
Пример № 8.
Вычислить:
.
Решение.
Используя тригонометрическое преобразование, имеем:
.
Пример № 9.
Вычислить:
(неопределенность
).
Решение.
Используя тригонометрические преобразования, имеем:
.
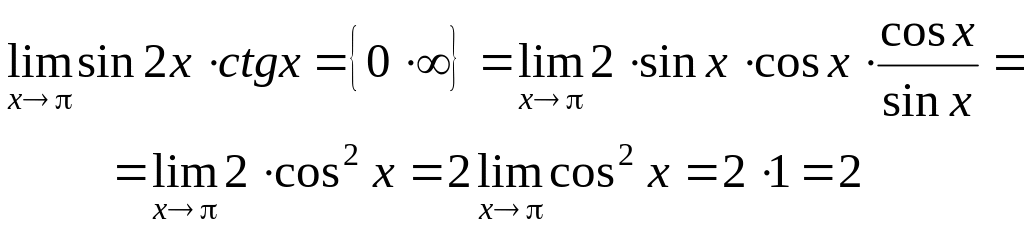Неопределенность вида
.
Раскрывается с помощью второго
замечательного предела.
.
Пример № 10.
Вычислить:
(неопределенность
).
Решение.
Для решения используем
второй замечательный предел
.
Имеем:
.
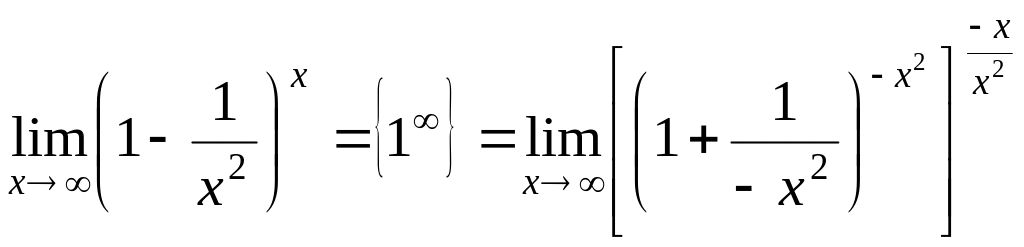Сделаем замену
.
Т. к.
,
то и
.
Тогда:
.
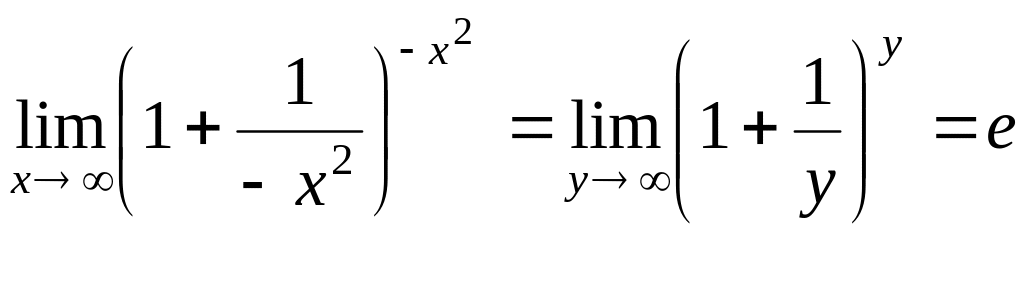Отсюда:
.
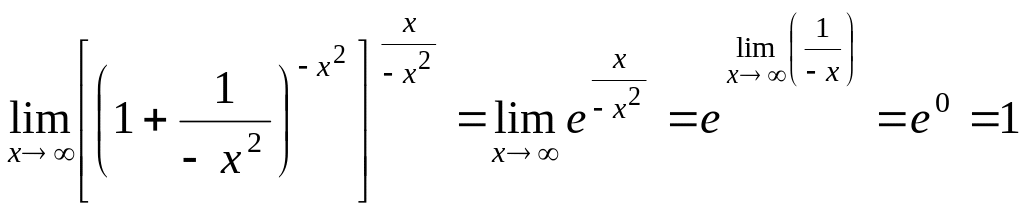Пример № 11.
Вычислить:
(неопределенность
).
Решение.
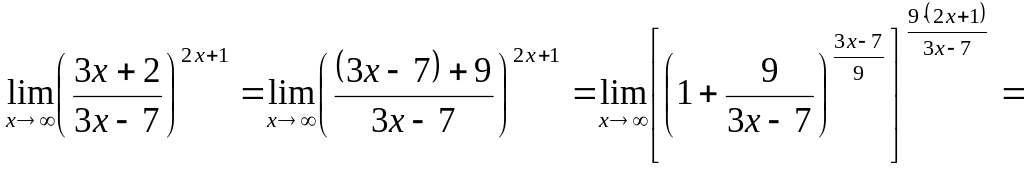
