Знаходження статистичного (вибіркового) коефіцієнта кореляції.

Розглянемо другу задачу теорії кореляції.

Величиною, що виражає прямолінійну залежність між ознаками та , є коефіцієнт кореляції, який обчислюється за формулою

.

Властивості коефіцієнта кореляції:

1. , тобто . Якщо , то кореляція додатня (при зростанні значення ознаки значення ознаки теж зростають); якщо , то кореляція від’ємна (із зростанням значення ознаки значення ознаки спадають).

2. Якщо , то ознаки та пов’язані функціональною залежністю (лінійною).

3. Якщо , то між ознаками та існує кореляційна залежність, при чому цей зв’язок тим тісніший, чим ближче до 1.

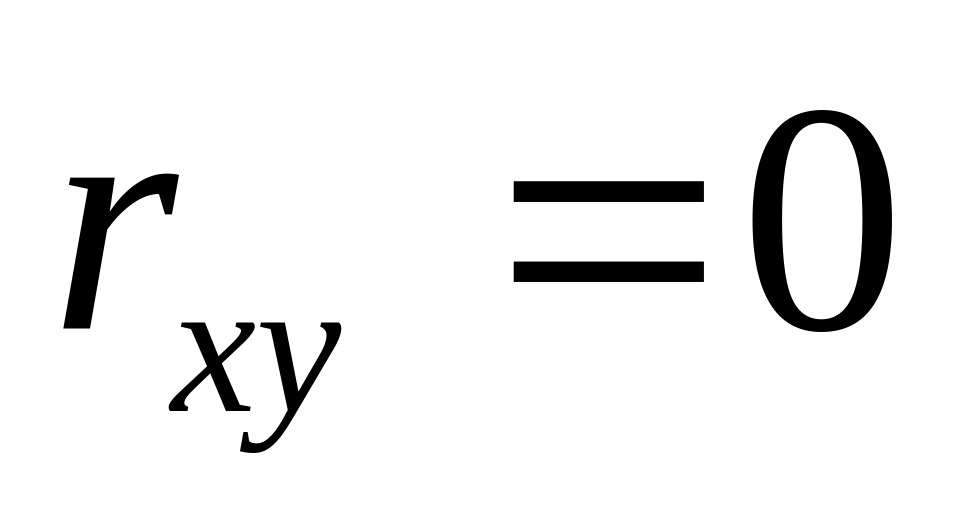4. Якщо , то ознаки та - незалежні, тобто не зв’язані кореляційною залежністю.

ЗАВДАННЯ. На основі вибірки обсягу ( - задається), здійсненої з таблиці генеральної сукупності(зріст і вага учнів випускних класів), визначити і знайти форму зв’язку між заданими ознаками. Обчислити коефіцієнт кореляції, за допомогою якого зробити висновки про силу кореляційного зв’язку між ознаками.

Статистична перевірка гіпотез

Мета: Ознайомити з статистичними гіпотезами та їх різновидами, з похибками перевірки гіпотез, з критеріями узгодження для перевірки гіпотез. Навчити застосовувати критерій Пірсона для перевірки гіпотези про нормальний закон розподілу генеральної сукупності.

1. Статистичні гіпотези та їх різновиди.

Однією з основних задач математичної статистики є визначення закону розподілу генеральної сукупності або параметрів цього закону розподілу за статистичними даними. У природознавстві, техніці, економіці часто для з’ясування справедливості того чи іншого факту звертаються до висловлювання гіпотез, які можна перевірити статистично, тобто спираючись на результати спостережень у випадковій вибірці.

Метод статистичних гіпотез є одним із найважливіших і найцікавіших, з професійної точки зору, методів статистичного дослідження властивостей генеральної сукупності на основі вибірки у математичній статистиці. Універсальність цього методу полягає в тому, що він дозволяє проводити статистичне дослідження розподілів генеральної сукупності, будувати їх та знаходити точкові оцінки параметрів цих розподілів.

Історія перевірки статистичних гіпотез веде початок з XVIII ст. Самий перший приклад перевірки статистичної гіпотези з’явився в роботі, що датована 1710р. і написана Дж. Арбутнотом (1667-1735).

Статистичною гіпотезою називають будь-яке твердження про властивості ознаки генеральної сукупності, що перевіряється на основі вибірки. Статистичну гіпотезу позначають через H₀. Її називають основною (нульовою) гіпотезою.

Поряд із припущеною гіпотезою завжди можна розглядати протилежну їй гіпотезу. Це є альтернативна (конкуруюча) гіпотеза H₁, яка містить твердження про ту саму властивість ознаки генеральної сукупності, яке відмінне від змісту гіпотези H₀. Наприклад: якщо H₀: M(x)=6, то H₁: M(x) 6.

Гіпотезу називають простою, якщо вона містить лише одне припущення.

Гіпотезу називають складеною, якщо вона складається із скінченної або нескінченної кількості простих гіпотез.