4. Исследование тракта модулятор – демодулятор
4.1) Определим:
скорость АМ (амплитудной модуляции)
Скорость модуляции будет равна скорости выдачи кодовых символов канальным кодером
(бит/с)
тактовый интервал передачи одного бита
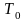
Тактовый интервал определяется как величина, обратная скорости модуляции
минимально необходимую полосу пропускания канала
Минимально необходимая полоса пропускания канала определяется в соответствии с теоремой Найквиста.
частоту несущего колебания
(Гц)
.
Аналитическое выражение ОФМ сигнала при двоичной модуляции:
Положим
:
2. Запишем аналитическое выражение, связывающее сигналы на входе и выходе.
Учитывая, что у нас гауссовский канал с неопределенной фазой, то выражения примут вид:
,
где
– сигнал на выходе,
– сигнал на
входе,
– шум.
,
где
коэффициента
передачи канала.
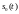и
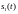– сигнал, соответствующий приему 0 и 1
.
Амплитуду
несущего колебания
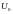можно рассчитать после вычисления
минимально необходимой мощности
единичного сигнала (пиковой мощности)
на передаче
.
Аналитическое выражение мощности единичного сигнала на передаче имеет вид:
Найдем
:
Найдем энергию единичного сигнала из формулы:
;
;
;
.
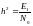Найдем мощность единичного элемента сигнала на приеме
,
откуда
(
),
(
);
При прохождении сигнала по каналу его амплитуда изменяется в раз. Поскольку мощность сигнала пропорциональна квадрату его амплитуды, то
(
);
Отсюда:
(
).
Запишем выражение, связывающее сигналы на входе и выходе:
.
3. Поскольку при ОФМ.информационный параметр сигнала определяется двумя соседними элементами на (n-1) – M интервале (–T;0) и на n-м интервале (0;T), то оптимальный алгоритм можно записать в виде
(1)
Приходящий сигнал s(t) на двух тактовых интервалах при ОФМ.можно представить в зависимости от символа, предаваемого n-м элементом, так:
,
(при
передаче символа 1);
(при
передаче символа 1);
(2)
где
– случайная
начальная фаза, неизвестная на приёме,
зависящая, в частности, от символа,
передававшегося (n
– 2)-м
элементом. Нетрудно видеть, что (2)
представляет собой двоичную систему
сигналов с равной энергией, ортогональную
в усиленном смысле на интервале
длительностью 2T,
а не T.
Поэтому вероятность ошибки при приёме
сигналов ОФМ.по
алгоритму (1) определяется на основании
,
(3)
но
с учётом того, что энергия сигнала на
интервале (–T;
T)
равна 2E:
,
(4)
где
параметр
–
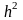отношение
энергии сигнала на интервале длительностью
T
к спектральной плотности мощности шума.
Как и следовало ожидать, вероятность
ошибки (4) несколько больше, чем вычисленная
для когерентного приёма двоичной ОФМ:.
,
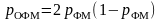(5)
однако различие между ними очень мало. Для схемной реализации алгоритм (1) можно упростить. Для этого поставим систему сигналов (2) в (1) и после сокращения одинаковых слагаемых приведём алгоритм приёма к виду
(6)
(7)
Полагая
фазу
хотя и случайной, но постоянной на
интервале (–T;
T),
можно легко показать, что левая часть
(6)
инвариантна
к значению этой фазы. Некогерентный
прием ОФМ.можно
реализовать в схеме с согласованным
фильтром и линией задержки (рисунок 5).
Приходящий сигнал поступает на фильтр
СФ, согласованный с элементом сигнала
длительностью
T.
Отклик
фильтра поступает на два входа
перемножителя, на
один из них
непосредственно, а на другой – через
линию задержки, обеспечивающую задержку
на время T.
z(t)
СФ
ФНЧ
РУ
x
к декодеру
z(t)
Задержка на T
Рисунок 3. Схема оптимального некогерентного приёма с согласованным фильтром и линией задержки для сигналов ОФМ.
Таким
образом, вблизи момента отсчёта на
перемножитель поступают напряжения,
соответствующие двум соседним элементам
сигнала – только что закончившемуся и
предыдущему, прошедшему через линию
задержки. Можно показать, что первое из
этих напряжений выражается формулой
,
а второе
После их
перемножения и фильтрации результата
в ФНЧ получаем напряжение
которое в
РУ.
Сравнивается
с нулевым порогом, т.е. реализуется
алгоритм (6). Описанную схему называют
схемой
сравнения фаз.
4. Найдем среднюю мощность сигнала на приеме
Она
рассчитывается по формуле:
,
где
– мощность
сигнала, соответствующего передаче
нуля на приеме. Для ОФМ
.
5.
Определим
пропускную способность непрерывного
канала связи
.
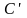Учтем, что для расчета
используется средняя мощность сигнала
на приемной стороне
.
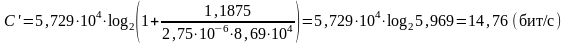
Вывод: Мы
рассчитали пропускную способность
непрерывного канала
.
Она больше скорости модуляции , что
говорит о правильно проделанных расчетах.
Так же это свидетельствует о том, что
сообщение будет проходить через декодер
без задержки.
6.
Ранее мы вычислили, что
.
Теперь определим, как
изменится
вероятность ошибки на выходе демодулятора
при использовании
других видов модуляции
при сохранении пиковой мощности сигнала:
Подставив численные значения, получим:
Итак, окончательно:
.
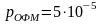Вывод: Вероятность ошибки при сохранении пиковой мощности для относительной фазовой модуляции меньше по сравнению с частотной и амплитудной модуляцией, следовательно, данный вид модуляции достаточно эффективен.