3. Исследование тракта кодер – декодер канала
Итак, для канального кодирования выбран код Хемминга (7,4).
3.1) При помехоустойчивом кодировании в сообщение целенаправленно вносится избыточность для обнаружения и (или) исправления ошибок в канале с помехами.
Кодирование осуществляется следующим образом: к четырем информационным разрядам добавляются три проверочных. В результате, получается, что каждый из семи символов участвует хотя бы в одной проверке.
Далее мы рассчитываем три проверочных разряда по формулам:
,
,
.
Затем рассчитанные проверочные разряды дописываются после четырех информационных. Так делается со всеми информационными разрядами и записывается готовая кодовая комбинация.
3.2) Рассчитаем:
избыточность кода
Для кода Хемминга (7,4), где
– общее число
разрядов кодовой комбинации;
– число информационных
символов;
– число проверочных
символов;
получим:
скорость кода
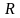
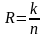
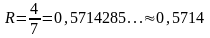(бит/с)
среднее число бит
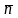
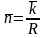
(кодовых
символов/символ источника)
(кодовых
символов/символ источника)
среднюю битовую скорость
(кодовых символов/с)
(кодовых символов/с)
3.3) Для определения обнаруживающей и исправляющей способности кода запишем таблицу кодирования по Хеммингу
Таблица №3
|
Информационная
комбинация
|
Кодовые комбинации
|
Вес,
|
0 |
0000 |
0000000 |
0 |
1 |
0001 |
0001011 |
3 |
2 |
0010 |
0010111 |
4 |
3 |
0011 |
0011100 |
3 |
4 |
0100 |
0100101 |
3 |
5 |
0101 |
0101110 |
4 |
6 |
0110 |
0110010 |
3 |
7 |
0111 |
0111001 |
4 |
8 |
1000 |
1000110 |
3 |
9 |
1001 |
1001101 |
4 |
10 |
1010 |
1010001 |
3 |
11 |
1011 |
1011010 |
4 |
12 |
1100 |
1100011 |
4 |
13 |
1101 |
1101000 |
3 |
14 |
1110 |
1110100 |
4 |
15 |
1111 |
1111111 |
7 |
Исходя из
результатов кодирования символов кодом
Хемминга, делаем вывод о том, что
минимальный вес кодовой комбинации
(число ненулевых символов), не учитывая
,
будет равно трём, т.е.
.
Теперь зная
,
определим:
исправляющую способность кода
п
ри
нечётном
;
при чётном .
обнаруживающую способность кода
3.4) Опишем процедуру декодирования в режимах обнаружения и исправления ошибок:
Рисунок 6. Декодер
На вход декодера
поступает последовательность кодовых
символов
,
некоторые из них, из–за наличия помех
в канале, могут быть приняты с ошибками.
Мы имеем дискретный канал, образованный
входом модулятора и выходом демодулятора,
являющийся дискретным симметричным
каналом без памяти. Для такого дискретного
канала
,
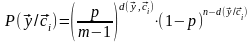где
;
–
передаваемая
кодовая комбинация;
– вектор ошибок;
– принятая кодовая
комбинация;
– расстояние по
Хеммингу между принятой комбинацией
и некоторой комбинацией
;
число символов, в
которых
и
отличаются, то есть
–
вес разности
;
–
вероятность ошибки
кодового символа в канале.
Правило максимального
правдоподобия при декодировании кодовой
комбинации имеет вид:
.
Учитывая
для дискретного симметричного канала
без памяти, получим
.
То есть в качестве решения выдаётся та
кодовая комбинация, которая ближе всех
к принятой комбинации
.
В результате получили, что:
1) В режиме обнаружения ошибки, декодер вычисляет синдром, если в синдроме нет единиц, то кодовая комбинация является разрешенной и декодер пропускает кодовую комбинацию, а если есть хотя бы одна единица, то комбинация является запрещенной.
2) В режиме исправления ошибки декодер сначала вычисляет синдром, затем по таблице синдромов обнаруживает ошибочный бит, затем инвертирует его.
3.5) Полагая, что декодер работает в режиме исправления ошибок, найдем:
вероятность ошибки на блок
(кодовую комбинацию из 7 бит) на выходе
декодера (неисправленную вероятность):
вероятность ошибки на бит
на выходе
декодера
Вывод:
Вероятность того, что декодер исправит ошибку в каждом блоке, достаточно велика, так как проведенные нами расчёты показали, что вероятность ошибки на блок и вероятность ошибки на бит достаточно малы. Следовательно, существует большая вероятность того, что переданное сообщение придёт без искажений.
3.6) Полагая, что декодер работает в режиме обнаружения ошибок, найдем:
вероятность ошибки на блок
на выходе декодера
(необнаруженную
вероятность):
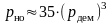
вероятность ошибки на бит на выходе декодера
.
Рассчитаем среднее число перезапросов на блок
:
В среднем, при
передаче
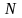блоков произойдёт
перезапросов. Однако, при повторной
передаче (перезапросе) также может быть
обнаружена ошибка, и будет сделан новый
перезапрос. Таким образом, получаем
рекуррентную формулу:
,
где
– число перезапросов в последовательности
длиной
блоков;
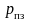– вероятность
перезапроса.
Отсюда среднее число перезапросов на один блок
Вероятность перезапроса равна вероятности того, что декодер обнаружит ошибку:
Подставив
численные значения, получим:
Тогда среднее число перезапросов на блок :
Вывод:
В режиме исправления ошибок вероятность ошибки на блок и вероятность ошибки на бит намного больше, чем в режиме обнаружения, значит, обнаруживающая способность кода Хаффмана эффективнее исправляющей. Однако, не всегда целесообразно использовать режим обнаружения ошибок, так как после обнаружения ошибки в блоке, он оказывается стёртым и уже не может быть выдан получателю. Обычно, его доставка осуществляется при помощи повторной передачи, на что требуется дополнительное время. При обнаружении требуется перезапрашивать ошибочные кодовые комбинации, что усложняет систему связи (нужен ещё один канал связи для передачи запроса).