4. Кодер

В кодере процесс кодирования осуществляется в два этапа. На 1-ом этапе производится безызбыточное (примитивное) кодирование каждого уровня квантованного сообщения a(t_i) к-разрядным двоичным кодом. На 2-ом этапе к полученной к-разрядной двоичной кодовой комбинации добавляется один проверочный символ, формируемый простым суммированием по модулю 2 всех информационных символов. В результате этих преобразований на выходе кодера образуется синхронная двоичная случайная последовательность b(t) (синхронный случайный телеграфный сигнал), состоящая из последовательности биполярных импульсов единичной высоты, причем положительные импульсы в ней соответствуют нулевым символам кодовой комбинации, а отрицательные – единичным.

Требуется:

1. Определить минимальное значение к, необходимое для кодирования всех L уровней квантованного сообщения a(t_i).

2. Определить избыточность кода с одной проверкой на четность Р_к.

3. Записать двоичную кодовую комбинацию, соответствующую передаче a_j-го уровня, считая, что при примитивном кодировании на 1-м этапе a_j-му уровню ставится в соответствие двоичная кодовая комбинация, представляющая собой запись числа в двоичной системе.

4. определить число двоичных символов, выдаваемых кодером в секунду V_k и длительность двоичного символа Т; найти скорость кодирования.

1. Найдем минимальное значение к, необходимое для кодирования всех L уровней квантованного сообщения a(t_i).

2. Определим избыточность кода с одной проверкой на четность.

3. Представим число j=55 в двоичной системе счисления:

С ледовательно к-6 информационных символов кодовой комбинации будут иметь вид:

Определим проверочный символ в₇ путем суммирования по модулю 2 всех к=6 информационных символов

Учитывая, что правило суммирования по модулю 2 имеет вид:

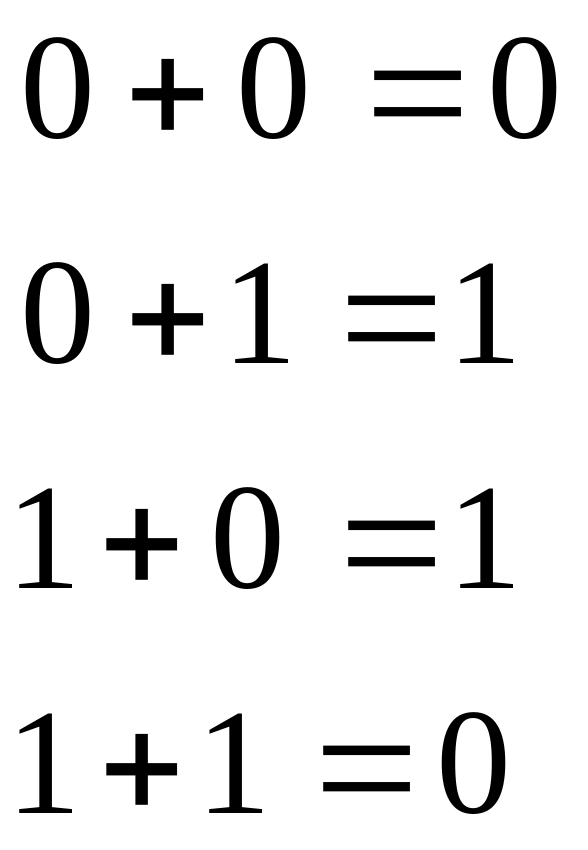получим, что в₇=1.

Т аким образом, искомая кодовая комбинация, соответствующая передаче а₅₅ уровня квантованного сообщения, будет иметь вид:

4. Число двоичных символов, выдаваемых кодером в секунду V_к, определяется числом отсчетов (1/Δt) и числом двоичных символов n=к+1, приходящихся на один отсчет.

Длительность двоичного символа определяется как величина, обратная V_k.

5. Модулятор

В модуляторе синхронная двоичная случайная последовательность биполярных импульсов в(t) осуществляет манипуляцию гармонического переносчика U₀cos(2πf₀t).

Параметры несущей: U₀=1B,

f₀=100V_k=8,434 ГГц.

Выражения сигналов: ;

.

Требуется:

1. Определить параметры несущей. Изобразить временные диаграммы модулирующего в(t) и манипулированного s(t) сигналов, соответствующих передаче а_j-го уровня сообщения а(t)/

2. Привести выражение и начертить график корреляционной функции модулирующего сигнала в(t) – B_в(τ).

3. Привести выражение и начертить график спектральной плотности мощности модулирующего сигнала в(t) – G_в(f).

4. Определить условную ширину энергетического спектра модулирующего сигнала ΔF_в(t) из условия ΔF_в=αV_k (где α выбирается от 1 до 3). Отложить полученное значение ΔF_в на графике G_в(f). Определить условную ширину энергетического спектра модулирующего сигнала методом равновеликого прямоугольника ( с помощью СПМ)

5. Записать аналитическое выражение модулированного сигнала s(t)=F[в(t)].

6. Привести выражение и построить график энергетического спектра модулированного сигнала G_s(f).

7. Определить условную ширину энергетического спектра модулированного сигнала ΔF_s. Отложить полученное значение ΔF_s на графике G_s(f).

1. Изобразим временную диаграмму модулирующего сигнала в(t).

b(t)

t

1 1 0 1 1 1 1

S(t)

t

Рис.5.1. Временная диаграмма манипулированного сигнала s(t)

2. Для определения функции корреляции рассмотрим два сечения в моменты t₁ и t₂ (t₂-t₁=τ) и найдем математическое ожидание произведения X(t₁)X(t₁+τ).

Если τ>Т, то эти сечения принадлежат разным тактовым интервалам и произведение может с равной вероятностью принимать значения +1 и -1, так что его математическое ожидание равно 0.

Если τ<Т, то возможны два варианта: случай А, когда они принадлежат одному интервалу и , следовательно, X(t₁)X(t₁+τ)=1, и случай В, когда они принадлежат разным тактовым интервалам и X(t₁)X(t₁+τ) может с равной вероятностью равняться +1 и -1. Поэтому при τ<Т математическое ожидание X(t₁)X(t₁+τ) равно вероятности р(а) того, что оба сечения оказались в одном интервале. Случай А имеет место, если первое из двух сечений отстоит от начала тактового интервала не более чем Т-|τ|, а вероятность этого равна (Т-|τ|)/Т.

Тогда функция корреляции имеет вид:

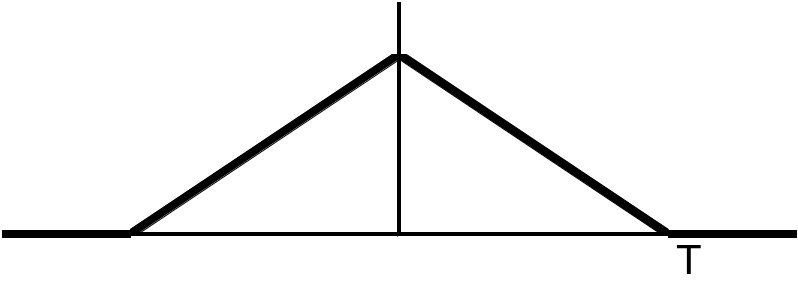
Рис. 5.3.

3. Найдем выражение для спектральной плотности мощности модулированного сигнала по теореме Винера-Хинчина:

;

Так как В(τ) - функция четная, то

;

Возьмем интеграл по частям:

П остроим график спектральной плотности мощности модулирующего сигнала:

Рис. 5.2. График спектральной плотности мощности модулирующего сигнала

4. Найдем условную ширину спектра сигнала. Под условной шириной спектра сигнала понимают полосу частот, в которой сосредоточена основная доля мощности сигнала. Чем больше выбранное значение α, тем большая доля мощности будет сосредоточена в этой полосе частот.

Пусть α=2

Определим долю мощности, сосредоточенную п полосе частот от 0 до .

;

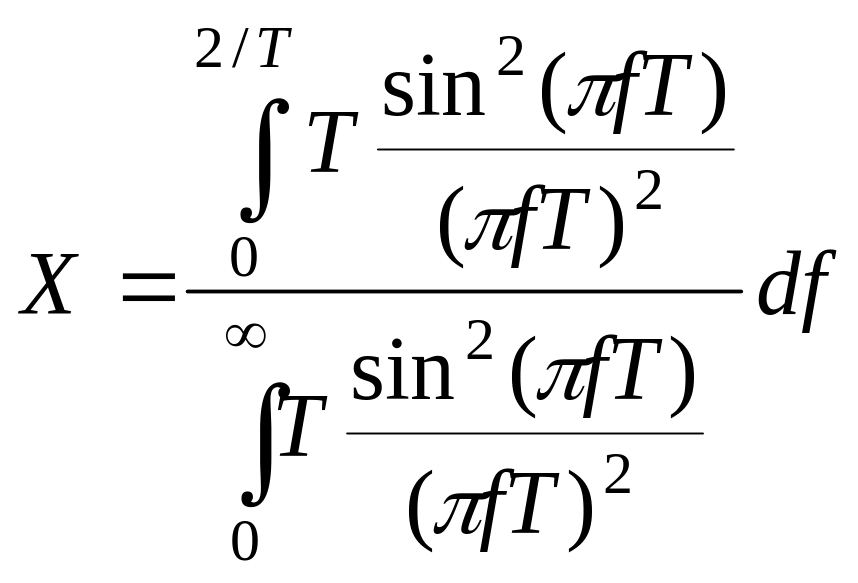
Рассмотрим по отдельности числитель и знаменатель этого выражения.

Возьмем этот интеграл по частям

U=sin²x; dU=sin2xdx; ; ;

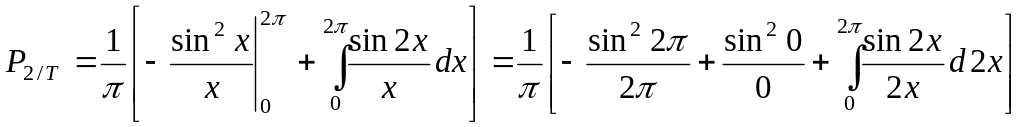
- интегральный синус; ;

Si(4π)=1.4922; Si(0)=0; .

Аналогично получим ,что .

; ; .

То есть получили, что 95% всей мощности сигнала приходится на полосу частот от 0 до ΔF_в.

5. После перекодировки последовательности в последовательность 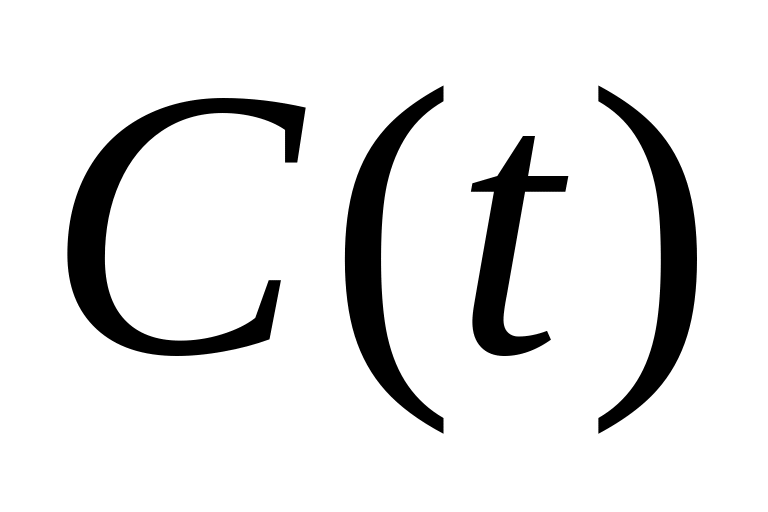по правилу нулевому символу соответствует 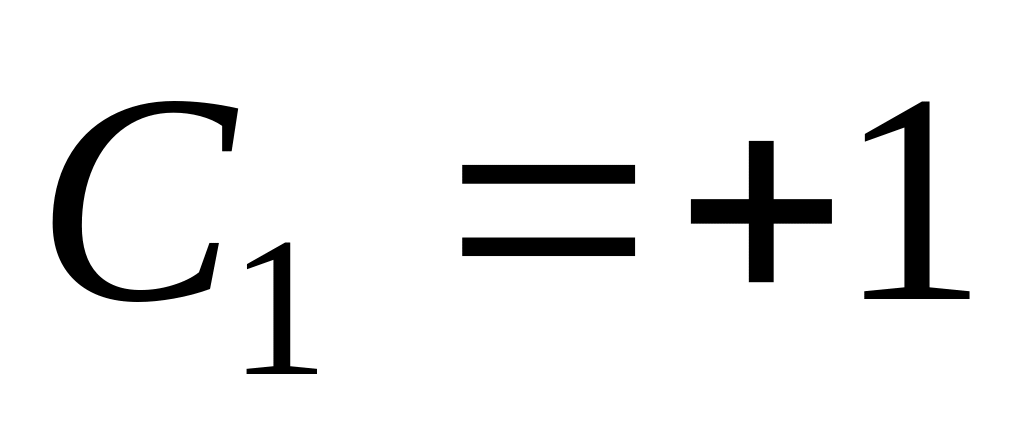, единичному - 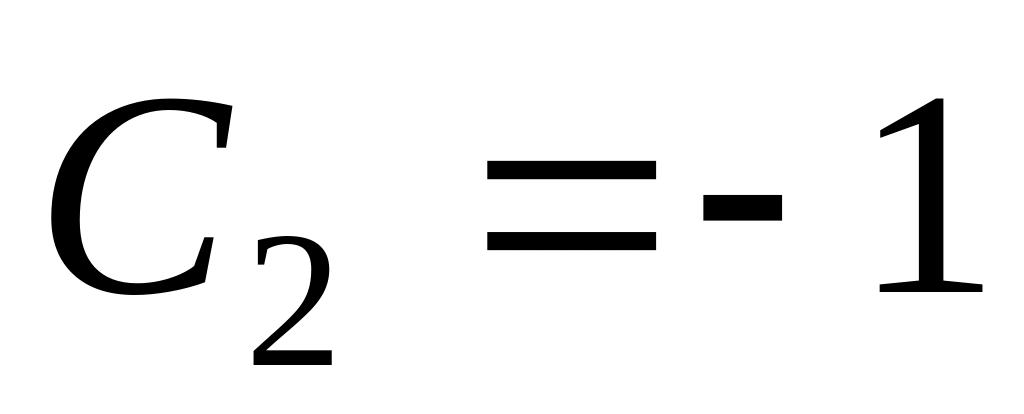. в дальнейшем происходит модулирование сигнала по правилу:

Пусть , тогда

при , тогда , следовательно,

при , тогда , следовательно,

6. При ФМ выражение энергетического спектра модулированного сигнала имеет вид:

Тогда построим график энергетического спектра модулированного сигнала G_s(f).

Р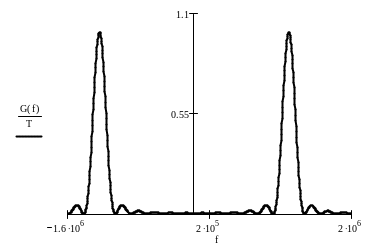 ис.5.3.

7. Условная ширина энергетического спектра будет в 2 раза больше условной ширины энергетического спектра модулирующего сигнала.

МГц