
- •II. Термодинамика растворов
- •8. Реальные растворы произвольной концентрации. Термодинамическая активность компонента
- •8.1. Определение активностей компонентов бинарного раствора по давлению паров над раствором
- •8.2. Определение активности растворителя по понижению температуры кристаллизации раствора
- •8.3. Определение активности компонента раствора по данным о химическом равновесии
- •8.4. Вычисление активности компонента бинарного раствора по известной активности другого компонента
- •8.5. Задачи для самостоятельного решения
8.5. Задачи для самостоятельного решения
2.120. Давления пара магния над расплавами Mg–Cu разного состава при 1000 K приведены в таблице. Определить активности магния относительно стандартного состояния «чистый жидкий магний» и характер отклонений от закона Рауля.
хMg |
1,000 |
0,936 |
0,765 |
0,581 |
0,330 |
0,224 |
рMg103, атм |
14,803 |
13,628 |
10,855 |
5,674 |
1,174 |
0,394 |
Ответ: аMg = 1,0; 0,9206; 0,7333; 0,3833; 0,0793 и 0,0266.
Mg = 1,0; 0,9836; 0,9586; 0,6590; 0,2403 и 0,1186. Отрицательные.
2.121. Давления пара серебра над расплавами серебро – золото при 1225 K приведены в таблице. Определить активности и коэффициенты активности серебра (стандартное состояние «чистое жидкое серебро»), а также характер отклонений от закона Рауля.
хAg |
1,000 |
0,775 |
0,620 |
0,388 |
0,195 |
pAg×106, атм |
2,635 |
1,806 |
1,243 |
0,671 |
0,192 |
Ответ: аАg = 1,0; 0,6854; 0,4717; 0,2546 и 0,0729.
gАg = 1,0; 0,9454; 0,7608; 0,6563 и 0,3737. Отрицательные.
2.122. Зависимость давления насыщенного пара (атм) чистого цинка от температуры выражается уравнением
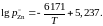
Вычислить активности и коэффициенты активности цинка при 973 K в сплавах Zn – Sn по экспериментальным данным, приведенным в таблице.
хZn |
0,748 |
0,495 |
0,484 |
0,231 |
рZn×102, атм |
6,197 |
4,697 |
4,609 |
2,507 |
Ответ: аZn = 0,7896; 0,5985; 0,5873 и 0,3194;
gZn = 1,0557; 1,2091; 1,2134 и 1,3829. Положительные
2.123. Температуры начала кристаллизации
хлористого магния в зависимости от
состава жидких солевых расплавов MgCl2
– PbCl2 приведены в
таблице. Определить активности и
коэффициенты активности хлористого
магния, если теплота плавления
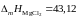 кДж/моль.
кДж/моль.
|
1,000 |
0,895 |
0,840 |
0,757 |
0,695 |
0,654 |
Т, K |
984 |
948 |
923 |
873 |
823 |
782 |
Ответ:
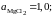 0,8192; 0,7064; 0,5120; 0,3569 и 0,2565;
0,8192; 0,7064; 0,5120; 0,3569 и 0,2565;
![]() 0,9153; 0,8410; 0,6764; 0,5135 и 0,3922.
0,9153; 0,8410; 0,6764; 0,5135 и 0,3922.
2.124. Температуры начала кристаллизации
магния из расплавов
Mg
– Cu приведены в таблице.
Определить активности и коэффициенты
активности магния. Какими отклонениями
от закона Рауля характеризуется поведение
магния в этой системе? Теплота плавления
магния
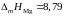 кДж/моль.
кДж/моль.
хMg |
1 |
0,945 |
0,900 |
0,863 |
0,855 |
Т, K |
923 |
873 |
823 |
773 |
758 |
Ответ: аMg = 1,0; 0,9365; 0,8700; 0,8007 и 0,7793.
gMg = 1,0; 0,9910; 0,9667; 0,9278 и 0,9115. Отрицательные.
2.125. В таблице
приведены составы равновесных жидких
и твердых растворов Сu
– Ag
при разных температурах. Вычислить
активности и коэффициенты активности
меди в жидких растворах Cu
– Ag,
если твердый раствор считать совершенным.
Теплота плавления меди
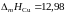 кДж/моль.
кДж/моль.
Т, K |
1356 |
1273 |
1223 |
1173 |
1123 |
1051 |
|
1 |
0,973 |
0,964 |
0,958 |
0,954 |
0,951 |
|
1 |
0,890 |
0,800 |
0,690 |
0,560 |
0,399 |
Ответ: аСu = 1,0; 0,902; 0,8504; 0,800; 0,751 и 0,681.
Cu = 1,0; 1,014; 1,063; 1,160; 1,341 и 1,706.
2.126. При температуре 1873 K в несмешивающихся жидких серебре и железе концентрации меди равны соответственно 11,5 и 2,92 мол.%. Определить активности и коэффициенты активности меди в обоих растворах, если при этой температуре давление насыщенного пара чистой меди равно 1,23410–3 атм, а над раствором Fe – Cu указанной концентрации – 2,34410–4 атм.
Ответ: аСu
= 0,19;
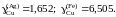
2.127. По данным таблицы о равновесных концентрациях кремния, распределенного при 1693 K между несмешивающимися железом и серебром, определить активности и коэффициенты активности кремния в железе, если коэффициент активности его в серебре в изученном интервале концентраций равен 0,155 (стандартное состояние – чистый кремний).
|
0,245 |
0,310 |
0,320 |
0,410 |
|
0,00138 |
0,0069 |
0,0076 |
0,0399 |
Ответ:
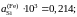 1,070; 1,178 и 6,185.
1,070; 1,178 и 6,185.
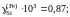 3,45; 3,68 и 15,08.
3,45; 3,68 и 15,08.
2.128. При 1888 K железо, равновесное с чистым монооксидом железа, содержит 0,249 мас.% кислорода. Вычислить активность и коэффициент активности монооксида железа в шлаке, содержащем 0,387 моля СаО; 0,171 MgO; 0,238 SiO2; 0,630 FeO; 0,037 Fe2O3 и 0,028 Cr2O3. Жидкое железо в равновесии с этим шлаком содержит 0,187% кислорода. Какими отклонениями от закона Рауля характеризуется монооксид железа в шлаке?
Ответ: аFeO = 0,751; gFeO = 1,777; положительные.
2.129. Использовав
приведенные в таблице данные о равновесии
реакции [C]Fe + 2Н2
= СН4
при 1273 K
(давления компонентов газовой смеси
выражены в атм), вычислить активности
и коэффициенты активности углерода в
аустените. Стандартное состояние –
гипотетический углерод и поэтому при
xC 0
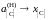 ,
,
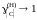 .
Каковы отклонения от закона Генри?
.
Каковы отклонения от закона Генри?
xC102 |
4,10 |
3,00 |
2,30 |
1,30 |
0,70 |
0,47 |
0,233 |
|
4,715 |
3,212 |
2,391 |
1,287 |
0,694 |
0,461 |
0,230 |
Ответ:
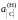 =
0,05481; 0,03278; 0,0244, 1,313, 0,708 далее
=
0,05481; 0,03278; 0,0244, 1,313, 0,708 далее
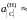 х[С].
х[С].
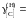 1,173; 1,093; 1,061 далее
1,173; 1,093; 1,061 далее
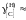 1. Положительные.
1. Положительные.
2.130. По данным о равновесии реакции 2(FeO) = O2 + 2Fе при 1373 K определить активности и коэффициенты активности монооксида железа в растворе FеО – MgO. Построить график зависимости активности монооксида железа от его концентрации.
хFeO |
1,000 |
0,815 |
0,740 |
0,615 |
0,54 |
0,43 |
0,225 |
|
13,46 |
13,56 |
13,63 |
13,69 |
13,74 |
13,83 |
14,18 |
Ответ: аFeO = 1,0; 0,8913; 0,822; 0,7674; 0,7244; 0,6531 и 0,4365.
gFeO = 1,0; 1,0936; 1,111; 1,248; 1,342; 1,519 и 1,940.
2.131. По данным о равновесии реакции (SiO2) +3C= SiC + 2СО при 1723 K определить активности и коэффициенты активности диоксида кремния в расплавах CaO – SiO2. Какими отклонениями от закона Рауля характеризуется диоксид кремния в этой системе?
(SiO2), % |
SiO2(тв) |
66,0 |
58,8 |
37,5 |
33,1 |
рCO, атм |
0,373 |
0,362 |
0,350 |
0,303 |
0,299 |
Ответ:
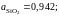 0,88; 0,66 и 0,643
0,88; 0,66 и 0,643
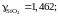 1,541; 1,838 и 2,035. Положительные.
1,541; 1,838 и 2,035. Положительные.
2.132. Для коэффициента активности цинка в сплавах кадмий – цинк при 435 °С было найдено
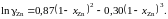
Найти, используя уравнение Гиббcа – Дюгема, зависимость от сосстава коэффициента активности кадмия в этих сплавах.
Ответ:
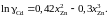
2.133.
Коэффициент активности цинка в
медноцинковых сплавах определяется
уравнением
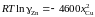 (R = 1,987 кал/мольK).
Найти, используя уравнение Гиббса –
Дюгема, зависимость от концентрации
коэффициента активности меди при 1500 K.
(R = 1,987 кал/мольK).
Найти, используя уравнение Гиббса –
Дюгема, зависимость от концентрации
коэффициента активности меди при 1500 K.
Ответ:
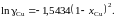
2.134. Коэффициент активности цинка в жидкой бронзе определяется уравнением (R = 1,987 кал/мольK). Вычислить парциальное давление паров меди при 1500 K над раствором, содержащим 40 мол.% Zn. При 1500 K давление пара чистой меди равно 710–4 атм
Ответ: 3,28110–4 атм.
2.135. Твердый сплав, содержащий 10 мол.% никеля и 90 мол.% золота, при 1000 K реагирует с водяным паром с образованием NiO. Реакция достигает равновесия, когда пароводородная смесь содержит 0,35 об.% водорода. Найти коэффициент активности никеля в растворе при 1000 K, используя следующие данные:
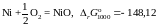 кДж;
кДж;
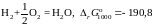 кДж.
кДж.
Ответ: 5,957.
2.136. Для системы Cd – Рb зависимость коэффициента активности кадмия от состава описывается уравнением
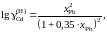
если за стандартное состояние выбрать гипотетический жидкий кадмий. Рассчитать активности кадмия в растворах, для которых хCd равно 0,2 и 0,4.
Ответ: 0,139 и 0,199.
2.137. Зависимость
активности монооксида железа в расплаве
FeO – Fe2O3
от ионной доли трехвалентного железа
при 1873 K описывается
уравнением
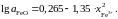 Определить состав
раствора, выбранного за стандартный.
Определить состав
раствора, выбранного за стандартный.
Ответ:
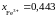 или 47 мас.% Fe2O3;
или 47 мас.% Fe2O3;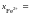 0,557 или 53 мас.% FeO.
0,557 или 53 мас.% FeO.
2.138. В расплаве
FeO – SiO2
при
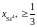 зависимость активности SiO2
от ионной доли кремния описывается
уравнением
зависимость активности SiO2
от ионной доли кремния описывается
уравнением
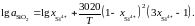
Определить при 1873 K
активность SiO2 в
расплаве FeO – SiO2
относительно твердого диоксида кремния,
если
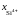 =
0,44. Известно, что при этой температуре
в насыщенном диоксидом кремния расплаве
содержится 52,9 мас.% SiO2.
=
0,44. Известно, что при этой температуре
в насыщенном диоксидом кремния расплаве
содержится 52,9 мас.% SiO2.
Ответ: 0,685.
2.139. При 1873
K насыщенный раствор Fе
– С содержит 5,3 маc.%
углерода. Определить активность
углерода по отношению к графиту (по
Раулю), если для стандартного состояния
«гипотетический углерод» (по Генри)
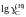 = 4,3хC
.
= 4,3хC
.
Ответ:
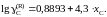
2.140. Давление насыщенного пара магния над расплавами магний – свинец при 1000 K приведено в таблице. Построить график pMg = f (xMg) и определить:
1) характер отклонений от закона Рауля и закона Генри;
2) активность магния в растворе с молярной долей магния 0,55.
xMg |
1 |
0,960 |
0,928 |
0,807 |
0,675 |
0,440 |
0,274 |
p×102, бар |
1,46 |
1,38 |
1,31 |
0,99 |
0,53 |
0,14 |
0,03 |
Ответ: отрицательные (Рауль), положительные (Генри), = 0,195.
2.141. Зависимости давлений насыщенного пара серебра от температуры над раствором Ag – Au, содержащем 22,5 мол.% серебра, и над чистым серебром описываются уравнениями:
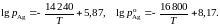
Определить температуру, при которой для раствора указанного состава для серебра соблюдается закон Рауля.
Ответ: 1550 K.
2.142. Зависимость парциальной молярной энтальпии и энтропии растворения таллия от состава расплавов Au – Tl при 1073 K приведена в таблице.
xTl |
0,20 |
0,40 |
0,60 |
0,80 |
0,90 |
|
398 |
293 |
163 |
84 |
63 |
|
19,01 |
11,30 |
5,95 |
2,30 |
1,00 |
Определить характер отклонений от закона Рауля и закона Генри для таллия.
Ответ: отрицательные
(Рауль), положительные Генри), так как
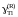 1.
1.
2.143. По зависимости давления насыщенного пара меди от состава железо – медных расплавов при 1823 K:
xCu |
1,000 |
0,883 |
0,792 |
0,626 |
0,467 |
0,217 |
0,061 |
0,023 |
0,015 |
|
7,29 |
6,72 |
6,47 |
6,34 |
5,98 |
5,32 |
3,09 |
1,33 |
0,87 |
вычислить
значения активностей и коэффициентов
активности меди, построить графики
зависимости их от состава и оценить
величину коэффициента активности меди
в бесконечно разбавленном растворе
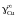 .
Стандартное состояние – чистая жидкая
медь.
.
Стандартное состояние – чистая жидкая
медь.
Ответ: aCu = 1; 0,922; 0,888; 0,870; 0,820; 0,730; 0,424; 0,182; 0,119;
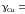 1; 1,044; 1,121; 1,389; 1,757; 3,363; 6,949; 7,930; 7,956;
1; 1,044; 1,121; 1,389; 1,757; 3,363; 6,949; 7,930; 7,956;
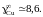
2.144. При температуре 1933 K железо, равновесное с чистым FeO, содержит 0,292 мас.% кислорода. Вычислить активность и коэффициент активности монооксида железа в шлаке следующего состава: 14,4 – CaO; 8,6 – MgO; 14,1 – SiO2; 54,0 – FeO; 4,7 – Fe2O3; 4,2 мас.% Cr2O3. Жидкое железо в равновесии с этим шлаком содержит 0,243 мас.% кислорода.
Ответ: 0,832; 1,674.
2.145. При 1913 K железо, равновесное с чистым FeO, содержит 0,269 мас.% кислорода. Вычислить активность и коэффициент активности монооксида железа в шлаке следующего состава: 18,52 – CaO; 6,86 – MgO; 13,34 – SiO2; 37,41 – FeO; 11,22 – Fe2O3; 10,64 мас.% Cr2O3. Жидкое железо в равновесии с этим шлаком содержит 0,181 мас.% кислорода.
Ответ: 0,673; 1,785.
2.146. По данным о
равновесии реакции
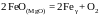 при 1573 K
при 1573 K
хFeO |
1 |
0,820 |
0,730 |
0,650 |
0,575 |
0,460 |
0,320 |
0,255 |
0,135 |
0,045 |
|
10,91 |
11,03 |
11,08 |
11,14 |
11,20 |
11,27 |
11,44 |
11,59 |
12,03 |
12,80 |
определить активности
и коэффициенты активности оксида железа
в растворах FeO – MgO.
Построить графики зависимостей
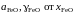 .
.
Ответ: aFeO = 1; 0,871; 0,822; 0,767; 0,710; 0,661; 0,543; 0,457; 0,275; 0,114;
FeO = 1; 1,062; 1,126; 1,181; 1,245; 1,436; 1,698; 1,793; 2,040; 2,522.
2.147. По данным о
равновесии реакции
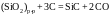 при 1773 K
при 1773 K
SiO2, мас.% |
Чистый SiO2 |
66,0 |
58,8 |
53,1 |
47,7 |
43,4 |
pCO, бар |
5,31 |
3,17 |
2,36 |
1,27 |
0,685 |
0,455 |
определить активности и коэффициенты активности кремнезема в растворах CaO – SiO2.
Ответ:
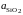 :
1; 0,356; 0,198; 0,057; 0,0166; 0,00734;
:
1; 0,356; 0,198; 0,057; 0,0166; 0,00734;
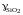 :
1; 0,553; 0,346; 0,111; 0,0362; 0,0176.
:
1; 0,553; 0,346; 0,111; 0,0362; 0,0176.
2.148. Равновесие реакции взаимодействия углерода,растворенного в аустените стали «Fe – Mn(4,04%) – C» при 1273 K
[C] + 2H2 = CH4
характеризуется
параметрами, приведенными в таблице.
Определить константу равновесия реакции,
активности и коэффициенты активности
углерода в трехкомпонентном твердом
растворе. Стандартное состояние –
гипотетический углерод, следовательно,
при х[С]
0
х[С] и
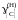
1.
1.
хС |
0,0530 |
0,0514 |
0,0495 |
0,0345 |
0,0263 |
0,0154 |
0,0075 |
, атм –1 |
6,04 |
5,55 |
5,31 |
3,17 |
2,26 |
1,27 |
0,601 |
Ответ: K
= 0,079 атм–1;
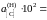 7,65;
7,03; 6,72; 4,01; 2,86; 1,61; 0,76.
7,65;
7,03; 6,72; 4,01; 2,86; 1,61; 0,76.
= 1,443; 1,367; 1,358; 1,163; 1,088; 1,044; 1,014.
2.149. Равновесие реакции [S]Fe + H2 = H2S изучалось при 1883 K (см. табл.).
хS102 |
7,15 |
5,56 |
4,15 |
3,09 |
2,34 |
2,03 |
1,93 |
1,72 |
1,18 |
0,79 |
|
8,50 |
7,12 |
5,51 |
4,40 |
3,30 |
2,91 |
2,82 |
2,52 |
1,73 |
1,18 |
Определить
константу равновесия реакции, вычислить
активности и коэффициенты активности
серы в жидком железе. Стандартное
состояние – гипотетическая сера и,
следовательно, при х[S]
0
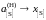 и
и
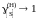 .
Построить графики зависимостей активности
и коэффициента активности от состава.
.
Построить графики зависимостей активности
и коэффициента активности от состава.
Ответ:
K
= 0,1467;
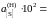 5,8;
4,9; 3,8; 3,0; 2,3; 2,0; 1,9; 1,7; далее
5,8;
4,9; 3,8; 3,0; 2,3; 2,0; 1,9; 1,7; далее
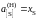 .
.
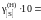 8,11; 8,73; 9,05; 9,71; 9,74; 9,77; 9,96; 9,99; далее
8,11; 8,73; 9,05; 9,71; 9,74; 9,77; 9,96; 9,99; далее
 .
.
2.150. При температуре 523 K коэффициент активности олова зависит от состава его сплавов с ртутью
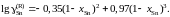
Определить зависимость коэффициента активности ртути от состава.
Ответ:
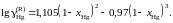
2.151. При температуре 1873 K коэффициент активности углерода зависит от состава железоуглеродистых расплавов
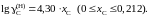
Определить зависимость коэффициента активности железа от состава раствора.
Ответ:
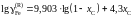 или
или
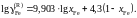
2.152. Зависимость активности углерода от состава аустенита описывается уравнением
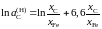
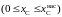 .
.
Определить зависимость активности g-Fe от состава.
Ответ:
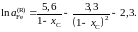
2.153. В расплавах Ag–Au при 1300 K парциальная молярная энтропия растворения серебра равна таковой для совершенного раствора S = – R(xAg lnxAg + xAulnxAu). По приведенным в таблице парциальным молярным теплотам растворения
хAg |
0,10 |
0,30 |
0,50 |
0,70 |
0,90 |
|
12,31 |
7,30 |
4,16 |
2,09 |
0,356 |
определить активности и коэффициенты активности серебра.
Ответ: аAg: 0,312; 0,589; 0,735; 0,849; 0,930;
Ag: 3,12; 1,965; 1,469; 1,213; 1,033.
2.154. Зависимости парциальных молярных энтальпии и энтропии растворения магния в расплавах Mg – Al от состава описываются уравнениями:
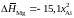 кДж/моль,
кДж/моль,
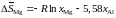 Дж/(мольK).
Дж/(мольK).
Определить активности и коэффициенты активности магния при 1000 K в растворах с молярной долей магния 0,1; 0,3; 0,5; 0,7; 0,9.
Ответ: аМg: 0,042; 0,197; 0,444; 0,727; 0,945; Mg: 0,42; 0,657; 0,888; 1,04; 1,05.
2.155.Энтальпия смешения раствора Mg – Ag DH= – 48,2 xMgxAg Дж/моль. Энтропия смешения равна энтропии смешения совершенного раствора. Определить при 1300 K активности и коэффициенты активности серебра в расплавах с молярной долей серебра 0,1; 0,3; 0,5; 0,7; 0,9.
Ответ: аAg: 0,0027; 0,0337; 0,164; 0,469; 0,861;
Ag: 0,027; 0,1124; 0,328; 0,670; 0,956.

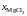
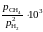
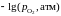
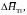 Дж/моль
Дж/моль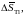 Дж/мольK
Дж/мольK pCu×104,
бар
pCu×104,
бар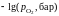
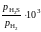
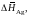 кДж/моль
кДж/моль