Объединенная классификация суждений:

А - общеутвердительные все S суть Р (SaP)

I - частноутвердительные некоторые S суть Р (SiP)

Е - общеотрицательные ни один S не суть Р (SeP)

О – частноотрицательные некоторые S не суть Р (SoP).

3.2.2. Распределённость терминов в категорических суждениях

Термин считается распределенным (или мыслится в полном объеме), если его объем полностью включается в объем другого понятия, или исключается из него. Термин считается нераспределенным, если его объем частично включается в объем другого понятия или исключается из него.

В простых категорических суждениях термины распределены следующим образом (+ означает распределен, - означает не распределен):

1. А (общеутвердительные):

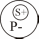
a) s+ s - распределен,

p- p – не распределен.

б) s+, p+ s и p распределены.

S+, P+

2. I (частноутвердительные)

а) s и p – не распределены

б) s- s – не распределен

p+ p – распределен

3. E (общеотрицательные)

s и p – распределены.

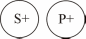
4) O (частноотрицательные)

s – не распределен

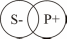
p – распределен

Распределенность терминов в суждениях может быть представлена в виде следующей таблицы:

	А	E	I	O
S	+	+	-	-
P	-	+	-	+

В общих суждениях субъект распределен, в частных - не распределен. Предикат в отрицательных суждениях всегда распределен, а в утвердительных он распределен, если РS.

3.3. Сложные суждения

Сложными называются суждения, состоящие из двух и более простых суждений. Простые суждения соединены между собой при помощи логических связок. Простые суждения со сложным субъектом или сложным предикатом могут быть преобразованы в сложные суждения. Например, “Иванов и Петров – свидетели” (SS¹ ) суть P можно представить: ab (“Иванов – свидетель и Петров – свидетель”).

3.3.1. Виды сложных суждений

Вид сложных суждений зависит от характера связи между входящими в него простыми суждениями. Среди сложных суждений различаются:

Соединительные (конъюнктивные) (утверждающие одновременное наличие двух и более ситуаций)

“Командир должен оценить обстановку и отдать приказ”(аb).

Разделительные (дизъюнктивные) суждения (в них утверждается или отрицается наличие одной из двух или более ситуаций).

Среди разделительных выделяют строго разделительные и просто разделительные. В (нестрого) разделительных суждениях утверждается наличие по крайней мере одной из двух ситуаций. “В центр города можно проехать на автобусе или на троллейбусе”.(аb). В строго разделительных утверждается наличие только одной из ситуаций (альтернатив). “Ночи бывают либо лунные, либо безлунные”( а b).

Условные (импликативные) суждения. В условных суждениях утверждается, что наличие одной ситуации вызывает наличие другой ситуации. “Если воду нагреть до 100 градусов, то она закипит”.(аb). Знак “если…, то…” выражает не только причинно-следственную связь, он может выражать и логическое следование, и другие связи. В современной логике различают условную связь “если…, то…” и так называемую материальную импликацию, отличающуюся от обычного выражения условной связки “если…, то…”(парадокс материальной импликации). В условном суждении выделяют основание и следствие: ab, где а - основание (антецедент), b – следствие (консеквент). Основание может быть необходимым и достаточным условием наступления следствия.

Суждения эквивалентности. В суждениях эквивалентности утверждается взаимная обусловленность двух ситуаций. Например, “Число делится на 2 и на 3, если, и только если оно делится на 6”( a↔b).

Суждения с отрицанием. В них отрицается наличие некоторой ситуации. “Неверно, что на улице хорошая погода” (а).

Истинность сложных суждений определяется истинностью входящих в них простых суждений; значимы также соединяющие их логические связки.