11. Закон изменения момента импульса (момент силы, момент импульса)

1. Момент импульса частицы

Пусть частица движется по некоторой траектории и в данный момент времени ее радиус-вектор равен, а импульс. Кроме импульса, существует еще одна векторная характеристика движения (динамическая переменная) - момент импульса.Моментом импульса частицы относительно точки (центра) О называется

векторное произведение радиус-вектора на импульс частицы:

.

Согласно определению, и, а его направление определяется по правилу правого винта.

Заметим, что величина зависит от выбора точки О; вообще говоря, ее можно выбрать где угодно, но обычно выбирают на оси вращения (если таковая имеется в наличии).

2. Закон изменения момента импульса. Момент силы

.

Вектор, равный векторному произведению радиус-вектора на силу,называется моментом силы.

Скорость изменения момента импульса частицы относительно некоторой точки равна моменту силы относительно той же точки.

Кратчайшее расстояние от точки О до линии действия силы l=r*sin называется плечом силы. Отсюда следует, что точку приложения силы (если, конечно, речь идет о твердом теле) можно сдвигать вдоль линии действия силы -- при этом ни l, ни не изменятся.

3. Момент импульса относительно оси

В дальнейшем нам придется столкнуться с проекцией момента импульса

на некоторую фиксированную (закрепленную) ось (например, ось z).

Эта величина называется моментом импульса относительно оси. Пусть частица массы m движется по окружности радиуса R вокруг этой оси.

Выберем точку О, относительно которой определяются вектора и, на оси z. Тогда. Величинаназываетсямоментом инерции частицы относительно оси.Таким образом, Lz=I, т.е. момент импульса относительно оси равен произведению момента инерции на угловую скорость вращения.

Закон изменения момента импульса относительно оси:

,

где Mz - проекция момента силы на ту же ось (или момент силы относительно оси).

Динамика системы частиц. Законы сохранения

Законы изменения и сохранения полного импульса системы частиц

В этой главе объектом изучения будет не одна частица, а система частиц. Система частиц может представлять собой любое агрегатное состояние вещества - газ, жидкость или твердое тело.

Систему всегда можно разбить на столь малые участки (линейные, плоские или объемные) с массой mi, что их размерами можно пренебречь и рассматривать эти участки как частицы (материальные точки).

Положение каждой из этих частиц задается радиус-вектором .

Масса всей системы определяется как m=. Если – плотность системы (тела), а dV – объем маленького участка, то его масса dm=dV, а масса всей системы m=где интеграл берется по всему объему системы.

На i-ую частицу системы, вообще говоря, действуют как внешняя сила  со стороны окружающих систему тел или полей, так и сумма внутренних сил со стороны всех остальных частиц системы. Поэтому закон движения i-ой частицы запишется в виде

Таких уравнений будет столько же, сколько всего частиц в системе. Суммируя эти уравнения для всех частиц системы и учитывая, что в силу третьего закона Ньютона , сумма всех внутренних сил, действующих на все частицы системы обращается в нуль

Таким образом, закон движения системы частиц или закон изменения полного импульса системы читается так:

Производная по времени (скорость изменения) полного импульса системы частиц равна результирующей внешних сил:

Уравнение можно записать и прочитать по-иному, если ввести еще одно понятие – импульс силы за время dt: это .

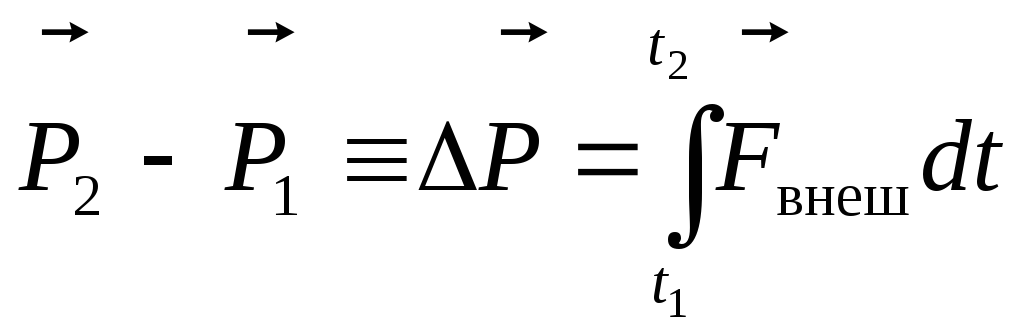
т.е. изменение (приращение) полного импульса системы за время t=t2 –t1 равно импульсу внешних сил за то же время.

Если все внешние силы, действующие на систему, уравновешиваются, т.е.  то система называется замкнутой. Для нее или–полный импульс замкнутой системы сохраняется. Это – закон сохранения импульса.

Часто , но действие сил длится столь малое времяt0, что импульс не успевает заметно измениться: . В этих случаях (быстрое столкновение, взрыв и т.п.) также можно применять закон сохранения импульса:

Заметим также, что возможны случаи, когда , но. Тогда сохраняется только проекция импульса на соответствующую ось: Px=const, что также широко используется в приложениях.