3. Сложное движение точки
Часто необходимо одновременно рассматривать движение точки или тела в различных системах отсчета неподвижной и движущейся. При этом необходимо найти аналитическую связь между описаниями движений и основными кинематическими характеристиками в этих системах отсчета. При этом движение точки относительно неподвижной системы отсчета будет как бы складываться из движения точки относительно подвижной системы отсчета и движения подвижной системы относительно неподвижной. Такое рассмотрение носит название сложное движение точки.
К примеру, человек идет по эскалатору метро. Его движение по отношению к Земле состоит из движения относительно эскалатора и движения эскалатора.
3.1 Относительное, переносное и абсолютное движения точки
Введем необходимые определения.
Движение точки, рассматриваемое одновременно в неподвижной и подвижной системах отсчета, называется сложным.
Движение точки относительно неподвижной системы отсчета называется абсолютным: скорость и ускорение точки в этом движении называются абсолютной скоростью – `
и абсолютным
ускорением –`
.Движение точки относительно подвижной системы отсчета называется относительным, а скорость и ускорение в этом движении – относительной скоростью –`
и относительным
ускорением –`
(индекс относительного движения
обусловлен английским словом “relative”
– относительный).
Движение подвижной системы отсчета относительно неподвижной называется переносным. Скорость и ускорение той точки подвижного пространства, с которой в данный момент совпадает движущаяся точка, называются переносной скоростью – `
и переносным
ускорением –`
.
3.2 Теоремы сложения скоростей и ускорений
Теорема сложения скоростей
Для установления зависимостей между абсолютными, относительными и переносными скоростями и ускорениями точки будем предполагать, что подвижная система отсчета Axyz движется поступательно вместе с полюсом А, и совершает вращение вокруг мгновенной оси АР с угловой скоростью ωе и угловым ускорением εе переносного движения (рис. 41).
z
A
Рис. 41
Движение точки М
относительно системы Axyz
задано с помощью радиус-вектора
,
а относительно неподвижной системы
отсчета – с помощью радиус-вектора
.
Движение начала подвижной системы
отсчета А относительно неподвижной
системы Oxyz определяется
радиус-вектором
.
Очевидно:
|
|
(48) |
.
Запишем:
|
|
(49) |
,где
-
орты подвижных осей координат.
Продифференцируем соотношение (48) с учетом (49) по времени:
|
|
(50) |
В соответствии с
определением скорости,
– абсолютная скорость точки М;
–
скорость начала (т. А) подвижных координат
или скорость точки М при переносном
поступательном движении,
- относительная скорость точки М.
Производные по времени от вращающихся геометрических векторов постоянной длины есть скорости движения их концов, которые определяются в соответствии с формулой (40):
|
|
(51) |
.Таким образом, второе слагаемое в правой части (50) приобретет вид:
- это скорость
точки М при переносном вращательном
движении с угловой скоростью ωе.
Тогда выражение (50) можно записать в
виде:
|
|
(52) |
.
В
последней форме записи (52) скорость
переносного движения
равна сумме скоростей поступательного
и вращательного движений.
Итак, сформулируем теорему сложения скоростей (52): вектор абсолютной скорости точки при сложном движении равен геометрической сумме ее переносной и относительной скоростей.
Теорема сложения ускорений
Если продифференцировать по времени полученное уравнение (52), то можно получить выражение, связывающее ускорения в неподвижной и подвижной системах отсчета. Оно носит название теорема о сложении скоростей, или теорема Кориолиса. Опустив необходимые преобразования, сформулируем ее в окончательном виде:
|
|
(53) |
.Абсолютное ускорение точки при сложном движении является векторной суммой трех ускорений – переносного, относительного и ускорения Кориолиса.
В формулировке теоремы обозначены:
- вектор абсолютного
ускорения;
- вектор переносного
ускорения, имеющий поступательную
,
вращательную
и осестремительную
составляющие;
- вектор относительного
ускорения, который в соответствии с
(16), (17) и (25) можно расписать в декартовых
и естественных осях подвижной системы
координат;
- т.н. «поворотное»
ускорение, названного в честь французского
механика Густава Гаспара Кориолиса
(1792 – 1843 г.г.).
Ускорение Кориолиса определяется по следующей формуле:
|
|
(54) |
.Ускорение Кориолиса есть удвоенное векторное произведение вектора угловой скорости переносного движения на вектор относительной скорости.
Как видно из определяющей формулы (54), вектор ускорения Кориолиса зависит как от угловой скорости переносного движения, так и от относительной скорости точки. Его величина определяется выражением:
|
|
(55) |
Из формулы следует,
что это ускорение будет отсутствовать
при
= 0,
= 0, или коллинеарности векторов
и
.
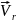
Рис.42
Направление вектора ускорения Кориолиса определяется по правилу векторного произведения (рис. 42).