
- •Основы теоретической механики кинематика
- •Содержание
- •Кинематика
- •1. Кинематика точки
- •1.1 Способы задания движения точки
- •1.2 Скорость точки
- •1.3 Ускорение точки
- •1.4 Теорема о разложении ускорения точки по естественным осям
- •1.5 Классификация движений точки по ускорениям
- •1.6 Частные случаи движения точки
- •2. Кинематика абсолютно твердого тела
- •Поступательное движение твердого тела
- •2.2. Вращательное движение твердого тела
- •2.3 Плоскопараллельное движение твердого тела
- •2.4 Сферическое движение твердого тела
- •3. Сложное движение точки
- •3.1 Относительное, переносное и абсолютное движения точки
- •3.2 Теоремы сложения скоростей и ускорений
- •4. Сложное движение твердого тела
- •4.1 Сложение поступательных движений
- •4.2 Сложение вращений вокруг параллельных осей
- •4.3 Сложение вращений вокруг пересекающихся осей
- •4.4 Сложение поступательного и вращательного движений
- •5. Кинематика зубчатых колес
- •5.1 Виды цилиндрических передач
- •5.2 Метод Виллиса
2.3 Плоскопараллельное движение твердого тела
Плоскопараллельное (плоское) движение твердого тела – такое движение, при котором все точки тела перемещаются в плоскостях, параллельных некоторой неподвижной плоскости.
Примером плоского движения тела является качение без скольжения колеса автомобиля по прямолинейному участку дороги, движение шатуна в кривошипно-ползунном механизме.
Закон плоскопараллельного движения
Точки тела, лежащие на одном перпендикуляре к неподвижной плоскости H, имеют одинаковые траектории, скорости и ускорения, так как этот перпендикуляр движется поступательно. Следовательно, для изучения движений точек этого перпендикуляра, достаточно изучить движение одной из них, например М (см. рис.20), а значит, для изучения движения плоскопараллельного движения тела, достаточно изучить движение точек тела, лежащих в сечении тела плоскостью П , параллельной неподвижной плоскости H, т.е. движение плоской фигуры S.

Рис.20
Положение
фигуры S в плоскости
П определяется положением любого
отрезка АМ (рис. 21), принадлежащего
плоской фигуре. В свою очередь, положение
отрезка АМ задается координатами одной
из его точек, например А, которую называют
полюсом, и ориентационным углом
 отрезка АМ.
отрезка АМ.


Рис. 21
Таким образом, для описания положение тела надо задать уравнения плоскопараллельного движения (или иногда говорят "плоского движения") в виде функций:
 ,
либо
,
либо
 (32)
(32)
при этом функции

 и описывают поступательное движение
фигуры S вместе с
полюсом А, функция
и описывают поступательное движение
фигуры S вместе с
полюсом А, функция
 - вращение фигуры вокруг полюса.
- вращение фигуры вокруг полюса.
Отсюда следует, что плоскопараллельное движение можно рассматривать как совокупность (сумму) поступательного движения, при котором все точки тела движутся так же, как полюс А, и вращения тела вокруг оси, проходящей через этот полюс.
Кинематические характеристики плоского движения тела
– скалярная
угловая скорость тела,
 – угловая скорость тела,
– угловая скорость тела,
 или
или
 – скалярное угловое ускорение тела,
– скалярное угловое ускорение тела,
 – угловое ускорение тела.
– угловое ускорение тела.
Векторы и всегда направлены перпендикулярно плоскости фигуры и совпадают по направлению при ее ускоренном движении и противоположны по направлению – при замедленном.
Скорость точки тела при плоскопараллельном движении
Радиус-вектор
точки М можно задать как
сумму двух векторов:
=
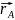 +
+ ,
где
–
радиус вектор точки М
в системе координат Аx₂y₂z₂.
Продифференцируем по времени обе части
этого выражения:
,
где
–
радиус вектор точки М
в системе координат Аx₂y₂z₂.
Продифференцируем по времени обе части
этого выражения:
 =
=
 +
+ , где
=
- скорость точки М,
=
, где
=
- скорость точки М,
= - скорость полюса А,
=
м
– скорость точки М относительно
системы координат Аx₂y₂z₂,
или скорость точки М
при
вращении фигуры вокруг полюса А,
которая определяется по формуле
- скорость полюса А,
=
м
– скорость точки М относительно
системы координат Аx₂y₂z₂,
или скорость точки М
при
вращении фигуры вокруг полюса А,
которая определяется по формуле

 = [
·
]. Тогда
=
A
+
.
(33)
= [
·
]. Тогда
=
A
+
.
(33)
Скорость точки при плоском движении равна геометрической сумме скорости полюса и скорости этой точки при вращении вокруг полюса.

Рис. 22
На рис. 22 представлена геометрическая интерпретация формулы (33)
 .
.
Причем угловая скорость плоской фигуры, вообще говоря, не зависит от выбора полюса.
Теорема о проекциях скоростей
При плоском движении тела, проекции скоростей двух точек тела на ось, проходящую через эти точки, равны между собой.
Для
доказательства воспользуемся формулой
B=
A
+ .
Проецирую это равенство на направление
АВ (рис.23) получим ПрAB
B
= ПрAB
A
+ ПрAB
.
.
Проецирую это равенство на направление
АВ (рис.23) получим ПрAB
B
= ПрAB
A
+ ПрAB
.




Рис. 23
Последнее слагаемое в этом соотношении равно нулю, так как вектор перпендикулярен АВ и, следовательно, ПрAB B = ПрAB A.
Теорема о распределении скоростей
Мгновенный центр скоростей (МЦС) – это такая точка плоской фигуры (присоединенной плоскости), скорость которой в данный момент времени равна нулю, при условии, что угловая скорость плоской фигуры не равна нулю. Обозначим эту точку Р (рис. 24). Ось, проходящая перпендикулярно плоской фигуре через МЦС, есть мгновенная ось скоростей (МОС).
Пусть P=0 , тогда точка Р – МЦС плоской фигуры. Точку А примем за полюс и выразим скорости точек В и Р.
B=
A+[
·
Вычтем почленно из первого равенства второе, тогда
|
Рис. 24 |
B=
[
·
]−
[
·
]
= [
· {
−
}]
= [
·
 ].
(34)
].
(34)
B= [ · ] – по форме записи эта формула аналогична формуле для определения скорости точки при вращательном движении тела.
Итак, если мгновенный центр скоростей плоской фигуры найден, то можно сформулировать нижеследующую теорему.
Скорости точек тела при плоском движении в каждый данный момент времени таковы, как если бы, начиная с данного момента времени, плоская фигура стала вращаться вокруг мгновенной оси скоростей с угловой скоростью .
Из этой теоремы следует, что модули скоростей прямо пропорциональны расстояниям точек до МЦС, векторы скоростей перпендикулярны отрезкам, соединяющим точки с МЦС. Распределение скоростей точек при плоском движении тела приведено на рис. 25.
|
⊥ РА;
ω
=
|
Рис. 25
Геометрические методы нахождения МЦС (рис.26 а, б, в)
а)
|
б) |
в) |
Рис. 26
Если A = B , то мгновенный центр скоростей плоской фигуры находится в бесконечности, мгновенная угловая скорость тела равна нулю. Скорости всех точек одинаковы (рис. 27) (ускорения точек различные). Тело находится в мгновенном состоянии поступательного движения.
|
Рис. 27 |
Физический метод нахождения МЦС
|
|
В некоторых случаях удается сразу указать точку плоской фигуры, скорость которой в данный момент времени равна нулю. В случае качения без скольжения одного тела по неподвижной поверхности другого точка Р соприкосновения поверхностей тел является МЦС (рис.28).
|
Рис. 28 |
Ускорение точки тела при плоскопараллельном движении
Из предыдущего параграфа известно, что = + [ ∙ ].
Продифференцируем
по времени обе части выражения
 =
=
 +
[
∙
]
+ [
∙
],
где
=
+
[
∙
]
+ [
∙
],
где
=
 ,
=
,
= [
·
],
=
.
,
=
,
= [
·
],
=
.
Тогда = A + [ · ] + [ [ · ]],
где [ [ · ]] – это двойное векторное произведение, раскроем его
[ [ · ]] = ( ∙ ) - ( · ), где ( ∙ ) = 0, т.к. ⊥ и ( ∙ ) = ω² . Следовательно, = А + [ · ] - ω² . (35)
Для точки В формула для определения ускорения имеет вид:
B
=
A
+ [
·
] - ω²
или
B
=
A
+ [
·
] + ω²
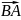 , (36)
где
А
- ускорение полюса А ;
, (36)
где
А
- ускорение полюса А ;
[ ∙ ] - = B - ускорение точки В при вращении вокруг полюса А.
 Ускорение
точки при плоскопараллельном движении
тела равно геометрической сумме ускорения
полюса и ускорения точки при вращении
вокруг полюса
B
=
A+
Ускорение
точки при плоскопараллельном движении
тела равно геометрической сумме ускорения
полюса и ускорения точки при вращении
вокруг полюса
B
=
A+ или
B
=
A
+ [
·
] - ω²
или
B
=
A
+ [
·
] - ω²
Геометрическая интерпретация формулы для определения B
|
Заданы A, и плоской фигуры (рис. 29) . Построить B.
|
B
=
A
+
 +
+

= [ · ] – касательное ускорение точки В при вращении вокруг полюса А, = ε · АВ – модуль его.
= ω² · - нормальное ускорение точки В при вращении вокруг полюса А, = ω² · AB – модуль его.
Теорема о распределении ускорений
Мгновенный центр ускорений (МЦУ) – это такая точка плоской фигуры, ускорение которой в данный момент времени равно 0.
Пусть точка Q – МЦУ плоской фигуры, аᵨ = 0. Точка А – полюс плоской фигуры.
В
=
А
+ [
·
]
- ω²
 ,
ᵨ
=
А
+ [
∙
,
ᵨ
=
А
+ [
∙
 ] - ω²
·
.
] - ω²
·
.
Вычтем из первого равенства второе, тогда получим
В = [ · ] - [ ∙ ] + ω² · - ω² · .
Преобразуем
это выражение, учитывая, что
–
=
 (рис. 30)
(рис. 30)
|
Тогда В = [ ∙ ] - ω² ·
или В = [ ∙ ] + ω² · .
|
Сравнивая это выражение с формулой для определения ускорения точки при вращательном движении твердого тела, сформулируем нижеследующую теорему.
Распределение ускорений точек тела при плоскопараллельном движении в каждый данный момент времени таково, как если бы, начиная с данного момента времени, плоская фигура стала вращаться вокруг МЦУ с угловой скоростью и угловым ускорением .
Рис. 31 |
tgμ
=
|
где μ – угол между направлением ускорения любой точки плоской фигуры и лучом, проведенным от данной точки до мгновенного центра ускорений. Этот угол откладывается от ускорения точки по направлению дуги для скалярного углового ускорения . (рис. 31).
Распределение ускорений точек тела при плоском движении представлено на рис. 32.
|
|
Примеры определения положения МЦУ плоской фигуры
Дано: A, , в данный момент времени. Построить МЦУ плоской фигуры.
Сначала
вычисляем tgμ =
, затем угол μ. От вектора
A
откладываем угол μ в направлении
дуги
и на этом луче находим точку Q,
откладывая от точки A
отрезок AQ =
 . Точка Q – МЦУ
плоской фигуры (рис. 33).
. Точка Q – МЦУ
плоской фигуры (рис. 33).

Рис. 33
Дано: ω=0 , ≠ 0 , , в данный момент времени. Построить МЦУ плоской фигуры.
Сначала
вычисляем tgμ =
, tgμ →
![]() , μ=90
, μ=90 .
.

Рис. 34
От направлений ускорений точек А и В проводим через точки лучи под углом 90 к этим ускорениям в направлении дуги . На пересечении лучей находится МЦУ плоской фигуры – т. Q (рис. 34).
Дано: ω ≠ 0, = 0 , B , A в данный момент времени. Построить МЦУ плоской фигуры.
Сначала вычисляем tgμ = , tgμ = 0 , μ=0º .
Точка Q – МЦУ плоской фигуры лежит на пересечении лучей,
проведенных из точек А и В и совпадающих с ускорениями этих точек (рис 35).

Рис. 35

 ],
P=
A+[
·
],
P=
A+[
· ].
].


 =
=

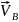 ⊥
РВ;
⊥
РВ; .
.




 Рис. 29
Рис. 29 Рис. 30
Рис. 30
 =
=
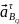 +
+

 =
BQ
=
BQ
 ,
, ,
,

 Рис. 32
Рис. 32 =
=
 .
.