2. Кинематика абсолютно твердого тела
Как уже отмечалось во введении, в абсолютно твердом теле неизменно сохраняется расстояние между любыми его точками, как бы само тело ни перемещалось.
Это означает, что точки абсолютно твердого тела движутся согласованно. В этом параграфе будут рассмотрены законы этих согласованных движений точек для различных случаев движений самих абсолютно твердых тел.
Поступательное движение твердого тела
Поступательным называют такой вид движения абсолютно твердого тела, при котором прямая, проходящая через любые две точки тела, при движении остается параллельной самой себе.
Иными словами, при поступательном движении пространственная ориентация тела не меняется.
Примеры поступательного движения тел: ступенька в движущемся эскалаторе, кабина в движущемся колесе обозрения, выдвигаемый ящик письменного стола.
Рис. 15
Пусть некоторое
тело, в котором выделены точки А и В
перемещается поступательно (рис.15). При
таком движении, согласно определению,
отрезок АВ не меняя пространственную
ориентацию, перемещается в новое
положение А′В′. Положения точек А и В
в пространстве определяются радиус-векторами
и
.
Тогда, в соответствии с правилом сложения
векторов:
|
|
(26) |
=
+
.
Поскольку отрезок
неизменен по величине и направлению,
все точки траектории В (линии ВВ′, или
годографа радиус-вектора
)
смещены от точек траектории А (линии
АА′, или годографа радиус-вектора
)
на длину АВ и в направлении
.
Это означает, что траектории точек А и
В одинаковы и линии ВВ′ и АА′ при их
наложении совпадут.
Продифференцируем (26) по времени:
Поскольку отрезок
- векторная константа, его производная
по времени равна нулю:
,
то выражение переходит в равенство
скоростей точек:
|
|
(27) |
=
.
Очередное дифференцирование (27) приводит к равенству ускорений рассматриваемых точек:
|
|
(28) |
=
.
Поскольку А и В – произвольно выбранные в теле точки, то из предыдущего следует, что при поступательном движении все точки абсолютно твердого тела двигаются по одинаковым траекториям и имеют равные скорости и равные ускорения в любой момент времени.
В этих условиях для описания поступательного движения тела достаточно знать, как движется хотя бы одна его точка, например точка А, координаты которой должны быть заданы как функция времени:
xA
,
yA
zA
– уравнения поступательного
движения тела.
Как будет следовать из анализа других видов движений твердого тела, только поступательное движение обладает указанными свойствами. Это значит, что кроме поступательного, при всех других видах движения точки тела двигаются с различными скоростями и ускорениями.
Таким образом, понятия «скорость тела» или «ускорение тела», движущегося не поступательно, не имеют смысла и их использовать некорректно.
2.2. Вращательное движение твердого тела
Вращение - это такой вид движения абсолютно твердого тела, при котором у тела есть хотя бы две неподвижные точки.
Прямая, проходящая через эти неподвижные точки, называется осью вращения тела.
И
з
геометрических соображений легко
показать, что все точки абсолютно
твердого тела, лежащие на оси вращения,
также неподвижны.
Рис
16
Пусть ось вращения тела связана с точками А и В (рис.16). Произвольная точка К абсолютно твердого тела может находиться на фиксированных расстояниях от точек А и В. Геометрическими местами точек, равноудаленных от них, являются сферы с радиусами АК и ВК соответственно. Их пересечение – окружность радиуса h, центр которой лежит на оси АВ. Таким образом, при вращении тела все точки тела описывают окружности с центрами, лежащими на оси вращения тела.
Скалярные характеристики вращательного движения
Угол поворота тела
При
повороте тела на некий угол φ
произвольная точка К переместится вдоль
окружности радиуса h
по дуге
,
причем связь длины дуги (криволинейной
координаты s) с углом
поворота тела определяется выражением:
|
|
(29) |
=
Путь, пройденный точкой тела при его вращении, равен произведению радиуса на угол поворота тела.
Здесь φ – угол поворота тела в радианах, определяет закон вращательного движения тела вокруг оси:
|
φ
|
(30) |
φ(t).
Угловая скорость и угловое ускорение твердого тела
Вектор
угловой скорости
есть скользящий вектор, направленный
по оси вращения в ту сторону, откуда
видно вращение тела против стрелки
часов (рис. 17а). Модуль угловой скорости
равен абсолютной величине скалярной
угловой скорости ω
|
|,
где
,
·
,
где
–
орт оси z.
Угловая скорость измеряется в рад/сек 1/сек, частота вращения в об/мин.
Если тело делает n об/мин, то угловую скорость в рад/сек найдем по формуле
ω
=
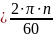. (31)
Вектор
углового ускорения
равен производной по времени от угловой
скорости
,
его модуль равен абсолютной величине
скалярного углового ускорения ε
|
|,
где
или
.
Вектор направлен по оси вращения и совпадает с вектором при ускоренном вращении (рис. 17 а, в) и противоположен ему при замедленном вращении
(рис. 17 б, г).
Рис. 17
Частные случаи вращательного движения твердого тела
Ускоренным называется такое вращение тела вокруг неподвижной оси, при котором модуль угловой скорости возрастает, при замедленном вращении – убывает.
Достаточные признаки ускоренного и замедленного вращательных движений тела получены аналогично соответствующим признакам ускоренного и замедленного движений точки и приводятся в таблице 2.
Таблица 2
Достаточные признаки ускоренного и замедленного вращений тела
-
Характер вращательного движения
З
н
а
к
+
-
+
-
+
-
-
+
ускоренное
ускоренное
замедленное
замедленное
Равномерное вращательное движение тела
При этом движении
тела
const,
- закон равномерного
вращательного движения тела.
Равнопеременное вращательное движение тела
При этом движении
тела
const,
– закон изменения
скалярной угловой скорости,
– закон
равнопеременного вращательного движения
тела.
Формулы в случаях 2 и 3 получены по аналогии с формулами равномерного и равнопеременного движения точки.
Скорость и ускорение точки при вращательном движении твердого тела
Рис. 18
Тело вращается вокруг оси z с угловой скоростью и угловым ускорением . Произвольная точка М движется по окружности радиуса R, ее радиус-вектор равен (рис. 18)
Скорость точки M , при движении по окружности, направлена по касательной к траектории в сторону движения, модуль скорости V=ω·R.
Покажем,
что
м
= [
].
Вычислим
модуль векторного произведения |[
]|
= ω
r
sin
α , но r
sin
α = = R, тогда |[
]|
= ω
R.
Построим вектор [ ]. Этот вектор перпендикулярен плоскости, в которой расположены векторы и , и направлен в ту сторону, откуда виден воображаемый поворот от к на наименьший угол против хода часовой стрелки, т.е. по касательной к окружности, которую описывает точка М.
Следовательно, = [ ]. Скорость точки М при вращательном движении тела равна векторному произведению угловой скорости тела на радиус-вектор точки.
Взяв
производную по времени от обеих частей
этого выражения, получим
=
=
=
+
.
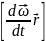Но
=
,
а
=
=
,
тогда
= [
]
+ [
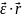– ускорение точки М.
Найдем модуль вектора [ ]. |[ ]| = ε r sinα = ε·R, и направлен вектор [ ] по касательной к окружности, описываемой точкой М.
Следовательно,
[
]
=
– касательное ускорение точки М.
Найдем
модуль вектора [
.
|[
|=ω·V·sin
=
R,
а направлен вектор [
по радиусу к центру окружности, описываемой
точкой М. Следовательно, [
=
–
нормальное ускорение точки М.
Модуль вектора ускорения точки М определяется по формуле:
a
=R
.
Так
как
=
+
,
то
= [
]+[
;
tgμ=
.
Распределения скоростей и ускорений точек при вращательном движении тела приведены на рис. 19.
Рис. 19