
- •Основы теоретической механики кинематика
- •Содержание
- •Кинематика
- •1. Кинематика точки
- •1.1 Способы задания движения точки
- •1.2 Скорость точки
- •1.3 Ускорение точки
- •1.4 Теорема о разложении ускорения точки по естественным осям
- •1.5 Классификация движений точки по ускорениям
- •1.6 Частные случаи движения точки
- •2. Кинематика абсолютно твердого тела
- •Поступательное движение твердого тела
- •2.2. Вращательное движение твердого тела
- •2.3 Плоскопараллельное движение твердого тела
- •2.4 Сферическое движение твердого тела
- •3. Сложное движение точки
- •3.1 Относительное, переносное и абсолютное движения точки
- •3.2 Теоремы сложения скоростей и ускорений
- •4. Сложное движение твердого тела
- •4.1 Сложение поступательных движений
- •4.2 Сложение вращений вокруг параллельных осей
- •4.3 Сложение вращений вокруг пересекающихся осей
- •4.4 Сложение поступательного и вращательного движений
- •5. Кинематика зубчатых колес
- •5.1 Виды цилиндрических передач
- •5.2 Метод Виллиса
1.4 Теорема о разложении ускорения точки по естественным осям
Ускорение точки при движении по любой траектории равно сумме касательного и нормального ускорений.
|
Рис. 8 |
Доказательство.
Известно, что . Определяем ускорение точки как производную от скорости по времени
 (24)
(24)
где первое
слагаемое
 – касательное
ускорение точки.
– касательное
ускорение точки.
Определим
величину и направление вектора
 .
.
B









 в
в
 произошло приращение
вектора
произошло приращение
вектора
 за промежуток времени
за промежуток времени
 ,
т.е.
,
т.е.
 ,
дуга
,
дуга
 равна приращению естественной координаты
(
равна приращению естественной координаты
( )
(рис. 9).
)
(рис. 9).
M
ε







A




Рис. 9
Вычислим

В
полученном выражении определим модуль
вектора
.
Из равнобедренного треугольника MAB
(рис. 9) найдем
 ,
,
 ,
тогда
,
тогда

 где
где
 кривизна
кривой в точке
M.
кривизна
кривой в точке
M.
Из
дифференциальной геометрии известно,
что
 следовательно,
следовательно,
 .
.
Покажем, что
перпендикулярен
.
Для этого скалярное произведение
 продифференцируем по
продифференцируем по

 или
или

Скалярное произведение двух, отличных от нуля, векторов равно нулю, если они перпендикулярны. Таким образом, вектор лежит в соприкасающейся плоскости, направлен в сторону вогнутости траектории и перпендикулярен к касательной, т.е. он направлен по главной нормали.
Вектор
 .
.
Итак, в выражении (24) , приведенном в начале доказательства теоремы, определены обе слагаемые.

Теорема доказана.
1.5 Классификация движений точки по ускорениям
1.
 - движение неравномерное, прямолинейное.
- движение неравномерное, прямолинейное.
2.
 - движение равномерное, криволинейное.
- движение равномерное, криволинейное.
Равномерным называют движение точки, при котором модуль скорости не изменяется.
3.
 - движение равномерное, прямолинейное.
- движение равномерное, прямолинейное.
4.
 - движение неравномерное, криволинейное.
- движение неравномерное, криволинейное.
1.6 Частные случаи движения точки
Равномерное движение точки

Закон
равномерного движения точки:

Ускоренное и замедленное движение точки
Ускоренным называют такое движение точки, при котором модуль скорости возрастает, при замедленном модуль скорости убывает.
Если
модуль скорости возрастает, то и квадрат
модуля скорости возрастает, но
 .
Вычисляя производную по времени от
.
Вычисляя производную по времени от
 , получим
, получим
 но
производная от возрастающей функции
больше нуля, тогда
но
производная от возрастающей функции
больше нуля, тогда
 т.е. знаки у скалярной скорости и
скалярного касательного ускорения
одинаковые. При замедленном движении
т.е. знаки у скалярной скорости и
скалярного касательного ускорения
одинаковые. При замедленном движении
 ,
т.е. знаки у названных кинематических
величин противоположные.
,
т.е. знаки у названных кинематических
величин противоположные.
Полученные результаты приведем в таблице 1.
Таблица 1
Достаточные признаки ускоренного и замедленного движений точки
|
|
|
Характер движения |
З н а к |
+ - + - |
+ - - + |
ускоренное ускоренное замедленное замедленное |
Получим
геометрические признаки ускоренного
и замедленного движений точки, для этого
продифференцируем по времени скалярное
произведение


При возрастании
модуля скорости
 больше нуля, при убывании модуля скорости
меньше нуля. Представим полученные
результаты на рис. 10 (движение точки
ускоренное) и рис. 11 (движение точки
замедленное).
больше нуля, при убывании модуля скорости
меньше нуля. Представим полученные
результаты на рис. 10 (движение точки
ускоренное) и рис. 11 (движение точки
замедленное).
|
|
Равнопеременное движение точки
Равнопеременным называют такое движение точки, при котором модуль скорости за любые равные промежутки времени изменяется на одну и ту же величину.
При
этом движении


 - закон изменения скалярной скорости
при равнопеременном движении точки,
график его изображен на рис. 12
- закон изменения скалярной скорости
при равнопеременном движении точки,
график его изображен на рис. 12


Рис. 12

 - закон равнопеременного
движения точки, (рис.13).
- закон равнопеременного
движения точки, (рис.13).

Рис. 13
Дано:
Определить:
Решение.
|
Рис. 14 |


где
 - скалярная угловая скорость поворота
радиуса.
- скалярная угловая скорость поворота
радиуса.
 – скалярное угловое
ускорение поворота радиуса.
– скалярное угловое
ускорение поворота радиуса.




где µ - угол наклона ускорения точки к радиусу.

 (рис. 8),
(рис. 8), .
.


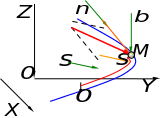


 Рис.
10
Рис.
10
 Рис.
11
Рис.
11 (рис.14).
(рис.14). .
.


