1.3 Ускорение точки

Ускорение точки при векторном способе задания движения

Рассмотрим изменение скорости точки при её перемещении по траектории.

Рис.7

Пусть  вектор скорости точки в положении М, а - в положении М₁, тогда приращение скорости за время t:

.

Перенеся вектор в точку М (рис.7), построим приращение вектора скорости .

Отношение  t   - среднее ускорение:

 

(14)

Направление вектора совпадает с направлением .  Предел соотношения (14) при t  0 есть ускорение точки М в момент t, или вектор ускорения:

(15)

Ускорение точки в данный момент времени равно производной по времени от скорости или второй производной от радиус-вектора.

Вектор лежит в плоскости, образуемой векторами и _, проведенным из точки М. При t  0  точка М₁ стремится к М и плоскость действия векторов скоростей при изменении направления  , будет менять свое положение в пространстве, поворачиваясь вокруг вектора  .

В пределе при t  0  и М₁  М векторы  и , как касательные к траектории в точках М и М₁, определят плоскость, которая называется: соприкасающаяся плоскость к траектории в точке М.

Таким образом, вектор ускорения  лежит в соприкасающейся плоскости и направлен в сторону вогнутости траектории.

Модуль ускорения измеряется в системе СИ – в м/с² (метр в секунду за секунду).

Ускорение точки при координатном способе задания движения

Если выражение (8) подставить в формулу (15), получим:

_.

Как и всякий вектор, вектор ускорения   можно написать в виде:

.

(16)

Сравнивая два последних выражения, представляющие один и тот же вектор, получим правила вычисления проекции вектора ускорения на оси координат: 

(17)

Проекции вектора ускорения точки на оси равны производным по времени от соответствующих проекций скорости на эти оси, либо вторым производным от соответствующих координат.

Модуль вектора ускорения вычисляется по формуле:

,

(18)

 

а его направляющие косинусы:

(19)

Ускорение точки при естественном способе задания движения

Пусть в момент времени t скалярная скорость точки , а в момент

t+∆t - + ∆ , за промежуток времени ∆t произошло приращение скалярной скорости ∆ .

Средним скалярным касательным ускорением в данный момент времени ∆t называют отношение приращения скалярной скорости к этому промежутку времени.

Скалярным касательным ускорением в данный момент времени называют предел среднего скалярного касательного ускорения точки при ∆t→0.

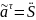или . (21)

Скалярное касательное ускорение точки в данный момент равно первой производной от скалярной скорости по времени или второй производной от естественной координаты по времени.

. (22)

Касательное ускорение точки равно произведению скалярного касательного ускорения на единичный вектор касательной.

(23)

Нормальное ускорение точки равно произведению модуля нормального ускорения на единичный вектор главной нормали.

Модуль нормального ускорения точки в данный момент времени

где – радиус кривизны траектории в точке M.

Касательное ускорение направлено по касательной к траектории, нормальное ускорение направлено по главной нормали в сторону вогнутости траектории. Касательное ускорение характеризует изменение модуля скорости, а нормальное – изменение направления скорости.