1.2 Скорость точки

 

Скорость точки при векторном способе задания движения

Пусть в некоторый момент времени t точка находится в положении М и её радиус-вектор равен = . За некоторое время t точка перемещается в положение M₁, определяемое соответствующим радиус-векторомr₁ = (рис.3).

 

 

Рис.3

В соответствии с правилом сложения векторов методом треугольника: 

,

откуда следует, что отрезок есть приращение радиус-вектора:

.

Вектор получил специальное название – перемещение.

Отношение    t  называется средней скоростью точки М за время t:

.

(6)

Средняя скорость точки является величиной векторной. Поскольку деление вектора на скаляр дает вектор, средняя скорость точки направлена по хорде (рис.4).

Рис.4

Предельное значение соотношения (6) при стремящемся к нулю интервале времени t  называется скоростью точки в данный момент времени (вектором мгновенной скорости):

.

Таким образом, вектор скорости есть производная по времени от радиус-вектора.

Краткое обозначение производной по времени – точка (˙) над символом дифференцируемой величины (в отличие от символа производной (′) по другой переменной в виде штриха).

Направление вектора скорости связано с предельным положением хорды (рис.3), т.е. направлен по касательной к траектории движения точки в сторону её движения.

При прямолинейном движении вектор скорости всегда направлен вдоль прямой, по которой движется точка, и может изменяться лишь по величине; при криволинейном движении кроме модуля изменяется и направление вектора скорости точки.

Модуль скорости имеет единицу измерения в системе СИ - м/с (метр в секунду).

Скорость точки при координатном способе задания движения

Векторная форма не всегда удобна для оценки количественных значений величин. Для нахождения численных оценок воспользуемся координатным способом задания движения точки. 

Подставляя выражение (4) в формулу (6), найдем

  _.

С другой стороны, векторV можно представить аналогично (4), т.е.

.

(8)

Отсюда найдем правила вычисления проекций вектора скорости на оси координат через закон движения точки, заданный координатным способом:

(9)

Таким образом, проекции вектора скорости точки на оси равны производным по времени от её координат на соответствующие оси.

Модуль вектора скорости через его проекции вычисляется по формуле

,

(10)

а направление - с помощью величины направляющих косинусов:

(11)

Скорость точки при естественном способе задания движения

Пусть в момент времени t ее естественная координата S, а в момент

t+∆t – S+∆S. За промежуток времени ∆t произошло приращение естественной координаты ∆S (рис.5).

(12)

 

Рис. 5

Средней скалярной скоростью точки за промежуток времени ∆t называют отношение приращения естественной координаты к этому промежутку.

Скалярной скоростью точки в данный момент времени называют предел средней скалярной скорости при ∆t→0.

Скалярная скорость в данный момент времени равна производной от

естественной координаты по времени.

Систему координат с началом в движущейся точке M на траектории,

осями которой служат касательная, главная нормаль и бинормаль, называют

естественным трехгранником (рис.6).

Рис.6

Касательная, главная нормаль и бинормаль – естественные оси, их единичные векторы , , , соответственно. Касательная и главная нормаль лежат в соприкасающейся плоскости.

- скорость точки в данный момент равна произведению скалярной скорости на единичный вектор касательной.

- модуль скорости точки равен абсолютной величине скалярной скорости точки.
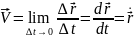