7.Нүктенің жазықтықтан қашықтығы
нүктесінің
жазықтығына дейінгі қашықтық
нүктесінен
жазықтыққа түсірілген перпендикулярдың
ұзындығына тең болады.
(7)
Егер
жазықтық нормаль теңдеумен берілген
болса,онда нормалауыш көбейткіш формуласы
ескеріледі
(7*)
Мысал.
нүктесінен
жазықтығына дейінгі қашықтықты тап.
Кеңістіктегі түзу
Кеңістіктегі
түзудің орны осы түзуде жататын бір
нүктесі және
векторы арқылы анықталады.
А Түзуге параллель немесе оның бойында жататын вектор түзудің бағыттауыш векторы деп аталады.
Олай болса,
түзудің векторлық
теңдеуі.
немесе
түзудің параметрлік теңдеуі
түзудің канондық теңдеуі
2.Кеңістіктегі түзудің жалпы теңдеуі. Кеңістікте түзу екі жазықтықтың қиылысуымен анықталатын болғандықтан, оның кеңістіктегі жалпы теңдеуі
жүйесі түрінде өрнектеледі.Бұл сәйкес жазықтықтар теңдеулері.Әруақытта түзудің жалпы теңдеуінен оның канондық теңдеуін алуға болады.Ол үшін түзуде жатқан кез келген нүктенің координаталарын табамыз.Ал теңдеулер жүйесіндегі z –ке кез келген мән беріледі.
Мысал.
түзу теңдеуін канондық теңдеу түріне
келтіру керек.
делік,
,
,
,
Сонымен
түзуде жататын
нүктесін таптық.
,
3.Кеңістіктегі түзулер арасындағы бұрыш.
,
канондық теңдеулерімен берілген өзара
қиылысатын екі түзу арасындағы бұрышты
табу керек.
Екі түзу арасындағы бұрыш
,
бағыттаушы векторларының арасындағы
бұрышқа тең.
Екі түзудің параллелдік
белгісі
перпендикулярлық
белгісі
Мысал.
және
түзулерінің арасындағы бұрышты тап.
,
Бұл
және
екі
нүкте арқылы өтетін түзу теңдеуі
болып табылады.
Мысал
және
нүктелері
арқылы өтетін түзу теңдеуін құрыңдар.
немесе
Мысал,
және
нүктелері
арқылы өтетін түзу теңдеуін құрыңдар.
(6) формуласына берілген координаталарын қойып табамыз:
немесе
Егер теңдеудің бөлімі 0-ге тең болса,
ол бөлшектің алымының 0-ге тең екендігін
көрсетеді.
5.Жазықтық пен түзу арасындағы бұрыш. Кеңістікте жазықтық жалпы теңдеуімен және түзу теңдеуімен берілсін.
Сонда жазықтық пен түзу
арасындағы бұрыш
Мысал:
жазықтығы
мен
түзу арасындағы бұрышты тап.
Жазықтықтағы екінші ретті қисықтар.
А
(1) түріндегі теңдеу екінші
ретті қисықтың жалпы
теңдеуі деп аталады, мұндағы теңдеу
коэффициенттері
нақты сандар.
Ш
еңбер
А Центр деп аталатын берілген нүктеден бірдей қашықтықта орналасқан жазықтықтағы нүктелер жиынтығын шеңбер деп атаймыз.
О1(a,
b) – шеңбер центрі, ал
-оның радиусы.
-
шеңбер теңдеуі. (2)
Егер Ох
осінде шеңбер центрі болса, онда
,
олай болса теңдеуді мына
түрде жазамыз:
( 3)
Егер Оу осінде шеңбер центрі
болса, онда
,
олай болса теңдеуді мына түрде жазамыз:
(4)
Егер шеңбер центрі координаталар
жазықтығының бас нүктесінде болса,
онда
,
,
олай болса теңдеуді мына түрде жазамыз:
()
2) Эллипс
А Жазықтықтағы фокус деп аталатын екі нүктеден қашықтықтарының қосындысы әрқашанда тұрақты шама аға тең болатын нүктелердің геометриялық орнын эллипс деп атайды.
А
ра
қашықтықтары с
болатын екі нүктені F1(с
)
және F2
(с
)
эллипстің фокустары
деп атайды.
F1Мr1
және F2Мr2
кесінділері фокальдік
радиустары.
ал 2а > 2с, олай болса а
> с
эллипстің канондық теңдеуі
.
Мұндағы
эллипстің үлкен жарты осі,
эллипстің кіші жарты осі.
А1(-а;
0), А2(а;
0), В1(0;
-b), В2(0;
b)
эллипстің координата
остерімен қиылысу нүктелері
эллипс төбелері
деп аталады.
эллипстің үлкен осі,
кіші осі.
АА, ВВ осьтері эллипстің симметрия осьтері, О нүктесі симметрия немесе эллипс центрі деп аталады.
эллипстің эксцентриситеті.
болғандықтан, мұндағы
.
эксцентриситет үлкейген
сайын, эллипс созыла береді, эксцентриситет
кішірейген сайын, эллипс сығыла береді.
Егер
болса, онда эллипс шеңберге айналады
Және
, ал
немесе
болғандықтан,
оң жақ және сол жақ
фокальдық радиустары
директрисалары. Егер
эллипстің
кез келген нүктесінен оның фокусына
дейінгі ара қашықтығы,
сол
нүктеден сәйкес директрисаға дейінгі
арақашықтығы болса, онда
қатынасы тұрақты шама және ол
.
Мысал
эллипстің теңдеуі берілген. Табу керек:
1) оның жарты осьтерінің ұзындығын
2) фокусының координаталарын
3) эллипстің эксцентриситетін
Шешуі: Берілген теңдеудің екі жағын 1176-ға бөліп, теңдеуді мына түрде жазамыз.
осыдан
,
яғни
Бұдан ,
Мысал
эллипс теңдеуі берілсін.
Фокустар аралығын, эксцентриситетін
және директриса теңдеуін табу керек.
Шығарылуы:Теңдеуді канондық
түрге келтіреміз:
,
;
;
,
,
(
).
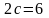Эксцентриситетін табамыз:
,
Директриса теңдеулерін
табамыз:
,
.