1.Векторлық алгебра және векторларға амалдар қолдану.

А. Бағытталған кесінді ( немесе реттелген қос нүкте) вектор деп аталады.

Белгіленуі . А нүктесі вектордың басы, В – ұшы деп аталады.

А. Вектордың бастапқы және соңғы нүктелері беттесіп кетсе, оны 0-дік вектор деп атайды. Белгіленуі

А. Вектордың басы мен ұшының арақашықтығы оның ұзындығы немесе модулі деп аталады. Белгіленуі 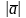немесе

А. Бір түзудің немесе параллель түзулердің бойында жатқан векторлар коллинеар деп аталады.

A B C

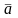
, - коллинеар векторлар,

А₁ В₁

, - коллинеар векторлар

А. Компланар векторлар деп бір жазықтықта немесе параллель жазықтықтарда жатқан векторларды атайды.

А. Тең векторлар деп өзара коллинеар, ұзындықтары тең және бағыттары бірдей векторларды айтады.Белгіленуі ,

2. Векторларға қолданылатын сызықтық амалдар.

А. векторын нақты λ санына көбейту деп мына шарттарды қанағаттандыратын векторын айтады.

1.

2. вектор векторына коллинеар

3. λ > 0 болса, және векторларының бағыттары бірдей

λ < 0 болса, және векторларының бағыттары қарама – қарсы

λ = 0 болса, және векторларының бағыттары анықталмаған.

Қасиеттері:

- сандар

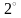+ = + ауыстырымдылық заң

терімділік заң

үлестірімділік заң

векторлар коллинеар

А .Бос векторлар деп параллель көшіруге болатын векторларды айтады.

Ол бастапқы нүктеге тәуелсіз, тек векторының ұзындығы мен бағытына ғана тәуелді вектор.

және векторлары координаталары бойынша жіктеліп берілсін.

1) ( аттас координаталары қосылады)

2) ( әрбір мүшесі сол санға көбейтіледі )

, нүктелері координаларымен берілсін. Сонда векторының координаталары былай табылады.

Мысал. және векторының координаталары

3. Векторлардың скалярлық көбейтіндісі және оның қасиеттері.

А. Екі вектордың скалярлық көбейтіндісі деп осы векторлардың модульдері мен олардың арасындағы бұрышының косинусының көбейтінділерін айтады.

( 1 )

Осыдан және векторларының арасындағы бұрыштың формуласы (1*)

Қасиеттері:

Скалярлық көбейтінді бір вектордың модулі мен екінші вектордың 1 – ші вектордағы проекциясына көбейтіндісіне тең.

( 2 )

Екі вектор өзара перпендикуляр болғанда ғана олардың скалярлық көбейтіндісі 0 – ге тең болады.

болса, онда олай болса

Вектордың скалярлық көбейтіндісінде ауыстырымдылық заң орындалады.

Көбейткіштердің біреуін сол санға көбейтсе болғаны

Үлестірімділік заңы орындалады.

Координаталарымен берілген вектордың скалярлық көбейтіндісі

осы векторлардың аттас координаталары көбейтінділерінің қосындысына тең.

Вектордың ұзындығының формуласы

Вектордың бағыттаушы косинустары , , ( 5 ) Олардың арасындағы байланыс

Координата өстерінің орттарын скалярлық көбейту мына түрде анықталады.

,

Ал векторлар координаталарымен берілсе

А. Екі және векторларының векторлық көбейтіндісі деп мына шарттарды қанағаттандыратын үшінші векторын айтамыз.

1)

2) ,

3) , , векторлары – реттелген оң үштік векторлар.

Қасиеттері:

ауыстырымдылық заң орындалмайды.

( векторларды қосуға қатысты үлестірімділік )

( санға көбейтуге қатысты терімділік )

болса, ( коллинеар )

, векторларының векторлық көбейтіндісі

Координата өстерінің орттарын векторлық көбейту мына түрде анықталады.

, , ,

Векторлардың аралас көбейтіндісі және оның қасиеттері.

А. Үш вектордың аралас көбейтіндісі деп алғашкы екі вектордың векторлық көбейтіндісін үшінші вектормен скалярлық көбейтіндісін айтады.

Қасиеттері:

,

ауыстырымдылық заң

вектордың тұрақты көбейткішін аралас көбейтінді таңбасының алдына шығаруға болады.

Координаталарымен берілген векторлардың аралас көбейтіндісі ,

Компланар векторлардың аралас көбейтіндісі 0 – ге тең, яғни

Жазықтықтағы аналитикалық геометрия

1. Екі нүктенің арақашықтығы.

Жазықтықта берілген және нүктелерінің арақашықтығын табалық. Вектор құрамыз:

( 10 )

Мысал. , нүктелерінің арақашықтығын тап.

2. Кесіндіні берілген қатынаста бөлу.

кесіндісі берілсін. Кесіндінің қатынасы шартын қанағаттандыратын осы кесіндінің нүктелерінің координаталарын табу керек.

, ,

болса, , кесіндіні қақ бөлу формуласы.

Жазықтықтағы түзулер

1. Түзудің бұрыштық коэффициентімен берілген теңдеуі.

Түзу берілсін, түзу мен О_х осінің арасындағы бұрышт φ-мен белгілейміз (көлбеулік бұрыш), b – түзудің ордината осін қиып өтетін кесінді.

А: Түзудің көлбеулік бұрышының тангенсі түзудің бұрыштық коэффициенті деп аталады және былай белгіленеді:

Түзудің бұрыштық коэффициентімен берілген теңдеуі

Берілген нүктеден өтетін және бұрыштық коэффициенті берілген түзу теңдеуі

Векторлар коллинеар болғандықтан, екі нүктеден өтетін түзу теңдеуі түрде табылады.

2.Түзудің жалпы теңдеуі (15)

Жеке жағдайда 1.С = 0 , түзу бас нүкте арқылы өтеді

2. А = 0 , немесе түзу О_х осіне параллель

3. В = 0 , түзу Оу осіне параллель

4. А = С = 0 , (немесе y = 0) түзу Ох осімен беттеседі

5. В = С = 0 , ( х = 0) түзу Оу осімен беттеседі

3.Түзудің кесінділік теңдеуі. а;b түзудің Ох,Оу осьтерімен қиылысқандағы кесінді ұзындықтары.

Екі түзудің арасындағы бұрыш .

Түзулер , жалпы теңдеулерімен берілсе

Е кі түзудің параллельдік белгісі ( )

перпендикулярлық белгісі немесе , ( )

4. Екі түзудің өзара орналасуы Түзулер жалпы теңдеулерімен берілсін: , Осы түзулердің коэффициентеріне байланысты:

1. түзулер қиылысады

2. Түзулер параллель

, ,( перпендикуляр)

,

3. Түзулер беттеседі

, (шексіз көп шешімі болады)

Мысалдар:

1) 4х - 5y + 7 = 0

3х + 2y+21 = 0 (18) формула бойынша , олай болса түзулер қиылысады.

2) 3х + 2y - 8 = 0

6х + 4y + 9 = 0 (18 ^*) формула бойынша түзулер параллель

3) 4х - 5y + 7 = 0

-12х + 15y - 21 = 0 (18 ^**) формула бойынша түзулер беттеседі