1.5 Направляющие системы и направляемые электромагнитные волны

1.5.1 Направляющие системы

Направляемые волны, в отличие от свободно распространяющихся в пространстве, могут существовать только при наличии направляющих элементов. Совокупность направляющих элементов образуют направляющую систему. Направляющие системы называют также линиями передачи энергии.

В се линии передачи можно разделить на два больших класса: линии передачи открытого типа и линии передачи закрытого типа. В линиях передачи закрытого типа вся энергия сосредоточена в пространстве, экранированном от внешнего металлической оболочкой. В линиях передачи открытого типа ЭМП, строго говоря, распределено во всем пространстве, окружающем линию. Однако открытые линии выполнены обычно т.о., что подавляющая часть энергии ЭМП сосредотачивается в непосредственной близости от линии.

1.5.2 Классификация направляемых волн

Направляемые волны делятся: на поперечные, электрические, магнитные и смешанные. Поперечными или волнами типа Т называются волны, у которых в продольном направлении /в направлении распространения энергии/ отсутствуют составляющие векторов напряженностей электрического и магнитного полей. Векторы и лежат в плоскости, перпендикулярной направлению распространения. Электрическими или волнами типа Е называются волны, у которых вектор электрического поля помимо поперечных составляющих, имеет продольную составляющую. Продольная составляющая вектора магнитного поля равна нулю. Магнитными или волнами типа Н называются волны, у которых вектор магнитного поля, помимо поперечных составляющих, имеет продольную составляющую. Продольная составляющая вектора электрического поля равна нулю. Смешанными (гибридными) называются волны, у которых векторы электрического и магнитного полей имеют как продольную, так и поперечную составляющую.

1.5.3 Связь между продольными и поперечными составляющими полей в регулярной направляющей системе

Рассмотрим произвольную бесконечно длинную направляющую систему, ориентированную вдоль оси Z . Будем полагать, что направляющая система не вносит потерь и однородна, т.е.:

– форма конечного сечения не зависит от координаты Z;

– параметры среды, в которой распространяется ЭМП, и граничные

условия, которым удовлетворят поле, не зависят от координаты Z .

При отсутствии сторонних источников должны удовлетворять однородным уравнениям Гельмгольца:

Зависимость и от координаты Z описывается множителем ,

В однородные уравнения Гельмгольца при и получим:

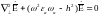(16)

Обозначение

(17)

где g - волновое число.

Уравнения (16) эквивалентно трем скалярным уравнениям для продольной и двух поперечных составляющих. Поперечные составляющие можно выразить через продольные с помощью соотношений, вытекающих из дифференциальных уравнений Максвелла.

Преобразуем однородные уравнения Максвелла:

(18)

Решая систему (18) относительно 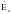получаем:

(19)

Аналогично, из (19)

(20)

Система уравнений (19)-(20) связывает поперечные и продольные составляющие поля в декартовой системе координат . Для выражения этой связи в произвольной системе координат перейдем к векторной форме уравнений .Введем вектор . Подставляя в это выражение вместо и их значения из (19) - (20) , получим :

.

Введя обозначение

и учитывая, что

получим 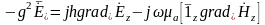(21)

Аналогично, получается равенство

Таким образом, для нахождения структуры полного поля необходимо решить с учетом граничных условий два дифференциальных уравнения:

(22)

и воспользоваться равенствами (21) для определения поперечных составляющих.

1.5.4 Критическая частота. Критическая длина волны

h, является вещественной величиной, если

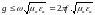(23)

и мнимой величиной, если

(24)

В первом случае фаза изменяется вдоль оси Z по линейному закону, что является признаком распространения волны с постоянной фазовой скоростью вдоль этой оси. Во втором случае вдоль оси Z фаза остается постоянной, а амплитуда убывает по экспоненте, что является признаком отсутствия переноса энергии вдоль направляющей системы.

Частота определяется из условия

(25)

называется критической.

(26)

Соответствующая этой частоте критическая длина волны равна:

(27)

Тогда (28)

где - волновое число, а - длина волны в среде с параметрами и .

Согласно (24) свободное распространение волны по направляющей системе имеет место лишь на частотах, превышающих критическую .

Назовем длиной волны в направляющей системе минимальное расстояние между поперечными сечениями, соответствующими различным значениям координаты Z , в которых колебания сдвинуты по фазе на . Так как зависимость составляющих поля от координаты Z описывается выражением: , то

(29)