Диаграмма направленности ээи.

Из формул (8), (9) следует, что амплитуды Е_т и Н_т зависят от координат θ и r:

.

При θ = 0 E_m = H_m = 0, при θ = 90° E_m и Н_т принимают максимальные значения. Это означает, что поле излучения ЭЭИ обладает направленностью, для характеристики которой вводится понятие диаграммы направленности (ДН).

Диаграмма направленности любого излучателя — это график зависимости амплитуд Е_т или Н_т от направления при фиксированном расстоянии (r = const). В сферической системе координат (рисунок 2) направление на точку наблюдения задается двумя угловыми координатами θ и φ. Обычно используют понятие нормированной, т. е. отнесенной к максимальной амплитуде, ДН.

Функция

F(θ,φ) =Е_т (θ, φ)/Е_т max = Sin θ

Рисунок 4 – Диаграмма направленности ЭЭИ

называется нормированной характеристикой направленности. Из полученной формулы следует, что поле ЭЭИ зависит только от меридионального угла θ и не зависит от азимутального угла φ. Графики F (θ, φ) в меридиональной (φ=const) (рисунок 4, а) и азимутальной (θ=const) (рисунок 4, б) плоскостях соответственно. Для построения ДН использована полярная система - координат, в центре которой помещен ЭЭИ.

2. Поверхностные волны Полное внутреннее отражение.

На практике широко используется явление полного отражения электромагнитных волн от границы двух диэлектриков или идеально проводящей поверхности, так как такие границы способны направлять электромагнитную энергию. Установим условия, при которых наблюдается полное отражение, и исследуем свойства возникающих при этом волновых процессов.

Полное отражение связано с исчезновением преломленной волны. Угол преломления изменяется от 0 до 90°, причем значение θ = 90° является предельным. Угол падения, соответствующий θ = 90°, принято называть граничным или критическим (φ_Кр). Из 2-го закона Снеллиуса следует, что sinφ_кр = n₁/n₂. Поскольку sinφ_Kp<1, то полученное равенство возможно, если в случае двух диэлектриков n₂<n₁, т.е вторая среда является оптически менее плотной, чем первая. Если φ>φ_кр, величина sin θ = (n₁/n₂) sinφ превышает единицу, теряя смысл функции геометрического угла и может рассматривать как некоторый параметр исследуемого процесса. Для нахождения коэффициентов отражения по формулам Френеля определим

(10)

который становится чисто мнимой величиной.

Известно, что _, получим:

(11)

Амплитуда отраженной и преломленной волн пропорциональна

, т.е.:

где — коэффициент отражения, — коэффициент преломления.

,

(12)

Решая эту систему, получим:

(13)

Коэффициенты отражения и преломления часто называют коэффициентами Френеля.

Подстановка полученного значения в (формулы 11 и 12) приводит к следующим результатам

.

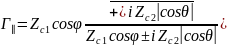Так как в числителе и знаменателе каждой из этих формул находятся комплексно-сопряженные выражения, модули которых равны, то , что свидетельствует о полном отражении волны от исследуемой границы а.

Таким образом, полное отражение электромагнитной волны от границы а двух диэлектриков возможно, во-первых, при углах падения, превышающих φ_кр, а во-вторых, если вторая среда является оптически менее плотной, чем первая.

Волна испытывает полное отражение также от границы идеального проводника. Это следует из (12,13), поскольку характеристическое сопротивление при σ₂=∞

Практический интерес представляет не только факт полного отражения, но и возникающие при этом волновые процессы. Установим характер этих процессов. С этой целью выполним анализ поля в первой и во второй средах, ограничиваясь, случаем нор­мальной поляризации. При параллельной поляризации основные особенности поля аналогичны.