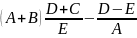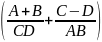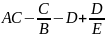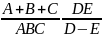Программная реализация методов математического моделирования
Цель работы – ознакомление с принципами программной реализации численных методов на примере оценки погрешности при помощи табличного редактора MS Excel.
Любое число, которое выдает нам эксперимент, это результат измерения. Данные, получаемые в эксперименте, всегда имеют некоторую неточность. Погрешность измерений диктуется ограниченной точностью приборов, допущениями при моделировании, округлениями при вычислениях. За счёт погрешности начальных данных формируется погрешность результата вычисления.
Погрешность измерения (абсолютная погрешность) – отклонение измеренного значения величины от её истинного (действительного) значения , выраженная в единицах измеряемой величины. Погрешность измерения является характеристикой точности измерения.
Относительная погрешность измерения – погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины. Относительная погрешность выражается в долях или процентах.
При сложении или вычитании двух чисел складываются их абсолютные погрешности. При умножении (делении) – складываются относительные погрешности.
Абсолютная погрешность обозначается греческой буквой Δ («дельта»); относительная погрешность — греческой буквой δ («дельта малая»). Если число обозначить буквой Х, то для перевода погрешностей можно воспользоваться формулой δ = Δ/Х.
Задание для моделирования
В программе моделируются два выражения: вычисление заданного математического расчёта; вычисление погрешности этого расчёта.
Пусть имеется несколько значений каких-либо параметров хi, используемых для расчёта либо измерения, и известны их относительные погрешности δi. Требуется определить величину погрешности в результате операций над этими параметрами. Математические выражения, значения их параметров и относительные погрешности этих параметров к данному заданию приведены соответственно в таблицах 2.1 и 2.2.
Для выполнения практической работы необходимо выбрать 3 произвольных уравнения из таблицы 2.1 и вычислить погрешности этих формул, применяя к каждой из формул данных из трех серий таблицы 2.2.
Таблица 2.1
№ |
|
№ |
|
1 |
|
6 |
|
2 |
|
7 |
|
3 |
|
8 |
|
4 |
|
9 |
|
5 |
|
0 |
|
Таблица 2.2
серия |
параметры |
||||
А |
В |
С |
D |
E |
|
1 |
15 ± 2% |
5 ± 1% |
2 ± 0,5% |
12 ± 1,5% |
9 ± 0,6% |
2 |
3 ± 0,2% |
4 ± 0,2% |
13 ± 1% |
2 ± 0,4% |
7 ± 0,3% |
3 |
1 ± 0,1% |
8 ± 1% |
5 ± 0,2% |
14 ± 3% |
12 ± 2% |
В качестве результата должны быть получены значения проведённого расчета и погрешности этого расчёта (таблица 2.3).
Таблица 2.2
серия |
Уравнение 1 |
Уравнение 2 |
Уравнение 3 |
||||||||
δ |
Δ |
Х |
δ |
Δ |
Х |
δ |
Δ |
Х |
|||
1 |
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
||
3 |
|
|
|
|
|
|
|
|
|
||
Пример расчета:
А – В × С
А = 5 ± 1%
В = 10 ± 2%
С = 20 ± 3%
1. δВ-С = 0,02 + 0,03 = 0,05
В×С = 10×20 = 200
2. ΔВ-С = 200×0,05 = 10
ΔА = 5 × 0,01 =0,05
3. Δ = 10 + 0,05 = 10,05
δ = 10,05 / (5 – 10 × 20) = 0,05
Контрольные вопросы
1. Дайте определение абсолютной погрешности?
2. Дайте определение относительной погрешности?
3. Какая зависимость между абсолютной и относительной погрешностью?
4. В чем измеряется абсолютная погрешность?
5. В чем измеряется относительная погрешность?
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Норенков, И.П. Основы автоматизированного проектирования: учеб. для вузов по напр.подготовки дипломированных спец. «Информатика и вычислительная техника» / И.П Норенков. - 2-е изд., перераб. и доп., доп. М-вом образов. РФ. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. – 336 с.
2. Вержбицкий, В.М. Основы численных методов / В.М Вержбицкий. – М.: Высшая школа, 2002. – 840 с.
3. Турчак, Л.И. Основы численных методов / Л.И. Турчак, П.В. Плотников. – М.: Физматлит, 2003. – 300 с.
4. Савельев, И.В. Курс общей физики / И.В. Савельев – М.: Наука, 1989. – 352 с.