Лабы / Lr-26

1

Лабораторная работа №26

ИССЛЕДОВАНИЕ ЛИНЕЙНЫХ ИНДУКТИВНО-СВЯЗАННЫХ КАТУШЕК

Цель работы – определение параметров линейных индуктивно-связанных катушек, исследование последовательного, параллельного соединения из и трансформаторного включения.

1. СВЕДЕНИЯ ИЗ ТЕОРИИ

Две катушки являются индуктивно-связанными, если изменение тока в одной из них приводит к появлению ЭДС в другой. Эта ЭДС называется ЭДС взаимной индукции.

Индуктивно-связанные катушки характеризуются параметрами L1, L2, M,

R1, R2, x1, x2, xM , где

L1 и L2 – индуктивности первой и второй катушек; M – взаимная индуктивность;

R1 и R2 – активные сопротивления катушек;

x1 2 f L1 – реактивное сопротивление первой катушки

В данной работе катушки соединяют последовательно, параллельно и по схеме трансформатора. При последовательном или параллельном соединениях возможны два вида подключения: согласное и встречное. В первом случае М>0, во втором М<0 [1].

Степень взаимно-индуктивной связи катушек характеризуется коэффициентом связи

Последовательное соединение катушек (рис.1)

Уравнение, составленное по II закону Кирхгофа в комплексной форме:

индуктивностью катушек. Из уравнения (2) определяется величина тока:

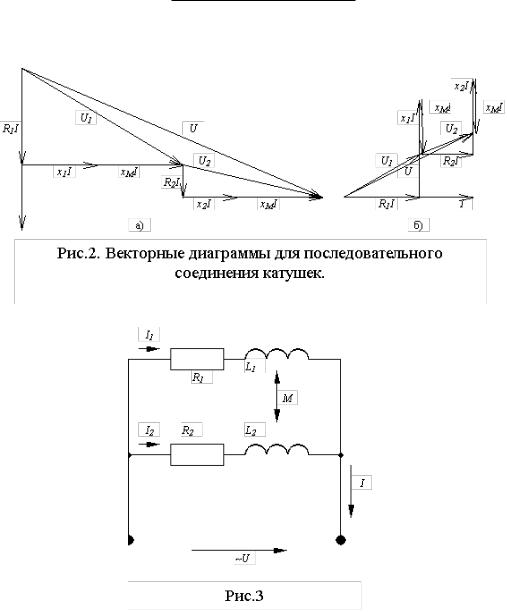
Векторные диаграммы для согласного и встречного включения, построенные согласно уравнению (2), приведены на рис.2 а,б.

Параллельное соединение катушек (рис. 3)

Уравнения, составленные по I и II законам Кирхгофа:

Решая систему (4), можно получить

Тогда

Знак «−» в числителе в уравнениях (5) и в знаменателе уравнения (6) перед слагаемым z M соответствует согласному, а знак «+» встречному включению.

Формулу для эквивалентной индуктивности Lэ получают из выражения (6). Например, при R1 R2 0 :

Векторные диаграммы для согласного и встречного включений приведены на рис.4а,б.

Трансформаторное включение (рис.5).

Уравнения, составленные по II закону Кирхгофа для цепей 1-ой и 2-oй катушек:

где Uн Rн I2 jxн I2 .

Решая уравнения (8) относительно I1 , получим

где Rвн - вносимое активное сопротивление из вторичной цепи в первичную; xвн - вносимое реактивное сопротивление из вторичной цепи в первичную.

Вносимое активное сопротивление всегда положительно (Rвн>0). вносимое реактивное сопротивление xвн в зависимости от характера реактивной составляющей сопротивления нагрузки может быть положительным или отрицательным. Векторная диаграмма для трансформаторного включения катушек при индуктивной нагрузке (φ > 0) приведена на рис.6.

2.ПРОГРАММА РАБОТЫ

1.Опытное определение параметров индуктивно-связанных катушек.

2.Исследование последовательного соединения катушек при их согласном и встречном включениях.

3.Исследование линейного трансформатора.

3.ВЫПОЛНЕНИЕ РАБОТЫ

П.1. программы. Исследуется схема (рис.7), зажимы второй катушки разомкнуты. С помощью ЛАТРа устанавливают по амперметру ток I, указанный преподавателем. Вольтметр сначала подключают к зажимам первой катушки и измеряют напряжений U1, затем - к зажимам второй катушки и измеряют U2. Показания амперметра, вольтметра и ваттметра (P1) заносят в табл.1.

После этого в цепь включают вторую катушку, оставляя зажимы первой катушки разомкнутыми. Установив ток I такой же величины, как в первом опыте, измеряют напряжение U2 на зажимах второй катушки и мощность Р2, затем напряжение U1 . Полученные данные заносят в табл.1.

5

Для первой катушки вычисления производят по формулам:

Коэффициент связи K вычисляют по формуле (1) .

П. 2 программы . Исследуется схема, представленная на рис.8. При замкнутом переключателе П по амперметру устанавливают заданную преподавателем величину тока. Переход от согласного включения к встречному осуществляется переключателем П. В обоих положениях переключателя поддерживают ток постоянной величины. Измеряют напряжения U1, U2, U и мощности P1, P2, Р при согласном и встречном включениях, подключая проводники «a», «б» поочередно к первой и второй катушке и ко входу цепи (выходные зажимы ЛАТРа). Данные опыта заносят в табл.2.