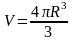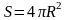Сфера и шар

Сфера – поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. Шар – тело, ограниченное сферой.

Объем шара	Площадь поверхности сферы

1. Сечение сферы плоскостью есть окружность, если расстояние от центра сферы до плоскости меньше радиуса сферы.

2. Сечение шара плоскостью есть круг.

3. Касательная плоскость к сфере – плоскость, имеющая со сферой только одну общую точку.

4. Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

5. Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.

6. Многогранник называется описанным около сферы, если сфера касается всех его граней.

7. Отрезки касательных к сфере, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр сферы.

8. Сфера вписана в цилиндрическую поверхность, если она касается всех ее образующих.

9. Сфера вписана в коническую поверхность, если она касается всех ее образующих.

задачи

1. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.

Ответ: 10.

2. Площадь большого круга шара равна 1. Найдите площадь поверхности шара.

Ответ: 4.

3. Во сколько раз увеличится площадь поверхности шара, если его радиус увеличить в два раза?

Ответ: 4.

4. Радиусы трех шаров равны 3, 4 и 5. Найдите радиус шара, объем которого равен сумме их объемов.

Ответ: 6.

5. Прямоугольный параллелепипед описан около сферы радиуса 2. Найдите площадь его поверхности.

Ответ: 96.

6. Куб вписан в шар радиуса . Найдите площадь поверхности куба.

Ответ: 24.

7. Прямоугольный параллелепипед описан около сферы радиуса 2. Найдите его объем.

Ответ: 64.

8. Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.

Ответ: 3.

9. Площадь поверхности прямоугольного параллелепипеда, описанного около сферы, равна 96. Найдите радиус сферы.

Ответ: 2.

10. Около шара описан цилиндр, площадь боковой поверхности которого равна 9. Найдите площадь поверхности шара.

Ответ: 9.

11. Во сколько раз площадь поверхности шара, описанного около куба, больше площади поверхности шара, вписанного в этот же куб?

Ответ: 3.

12. Куб вписан в шар радиуса . Найдите объем куба.

Ответ: 8.

Составные многогранники

задачи

1. На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите расстояние между вершинами A и C2 .

Ответ: 3.

2. Найдите угол CAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

Ответ:  60.

3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ: 18.

4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ: 132

5.  Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.

Ответ: 30

6. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ:8

7.Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ: 78

8. На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла ABB3.

Ответ: 2

10.  На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла C3D3B3.

Ответ: 3

11. Через среднюю линию основания треугольной призмы, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности призмы, если площадь боковой поверхности отсеченной треугольной призмы равна 37.

Ответ: 74.

12.  На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите квадрат расстояния между вершинами B2 и D3 .

Ответ: 11.