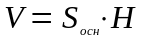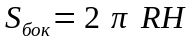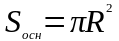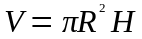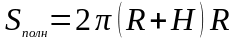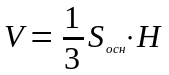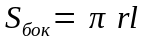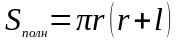Цилиндр

Цилиндр - тело, ограниченное цилиндрической поверхностью и двумя кругами с границами.

Объем тела	Площадь боковой поверхности	Площадь основания	Площадь полной поверхности

1. Образующие цилиндра - отрезки образующих, заключенные между основаниями.

2. Высота цилиндра - длина образующей.

3. Осевое сечение – прямоугольник, две стороны которого образующие, а две другие - диаметры оснований цилиндра.

4. Круговое сечение – сечение, секущая плоскость которого перпендикулярна к оси цилиндра.

5. Развертка боковой поверхности цилиндра - прямоугольник, представляющий собой два края разреза боковой поверхности цилиндра по образующей.

6. Площадь боковой поверхности цилиндра - площадь ее развертки.

7. Площадь полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований.

8. Около цилиндра всегда можно описать шар. Его центр лежит на середине высоты. 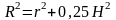, где R – радиус шара, r – радиус основания цилиндра, H – высота цилиндра.

9. В цилиндр можно вписать шар, если диаметр основания цилиндра равен его высоте, .

задачи

1. В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали?

Ответ: 3.

2. Найдите объем цилиндра, площадь основания которого равна 1, а образующая равна 6 и наклонена к плоскости основания под углом 30о.

Ответ: 3.

3. Цилиндр и конус имеют общие основание и высоту. Найдите объем цилиндра, если объем конуса равен 50.

Ответ: 150.

4. Воду, находящуюся в цилиндрическом сосуде на уровне 12 см, перелили в цилиндрический сосуд, в два раза большего диаметра. На какой высоте будет находиться уровень воды во втором сосуде?

Ответ: 3.

5. Площадь осевого сечения цилиндра равна 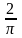. Найдите площадь боковой поверхности цилиндра.

Ответ: 2.

6. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 2. Найдите площадь боковой поверхности призмы.

Ответ: 32.

7. Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.

Ответ: 2.

8. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.

Ответ: 1,125.

9. В цилиндрическом сосуде уровень жидкости достигает 18 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого?

Ответ: 2.

Конус

Конус - тело, ограниченное конической поверхностью и кругом.

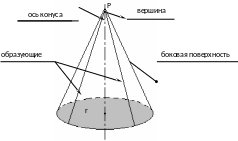
Объем тела	Площадь боковой поверхности	Площадь основания	Площадь полной поверхности

1. Площадь боковой поверхности конуса – площадь ее развертки.

2. Связь между углом развертки и углом 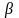при вершине осевого сечения .

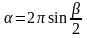1. Цилиндр и конус имеют общие основание и высоту. Найдите объем цилиндра, если объем конуса равен 50.

Ответ: 150.

2. Найдите объем конуса, площадь основания которого равна 2, а образующая равна 6 и наклонена к плоскости основания под углом 30о.

Ответ: 2.

3. Объем конуса равен 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите объем отсеченного конуса.

Ответ: 1,5.

4. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Ответ: 2.

5. Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на .

Ответ: 128.

6. Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 48.

Ответ: 16.

7. Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на .

Ответ: 9.

8. Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на .

Ответ: 16.

9. Конус получается при вращении равнобедренного прямоугольного треугольника вокруг катета, равного 6. Найдите его объем, деленный на .

Ответ: 72.