9. Расчет энтропии источника сообщения.

Энтропия источника сообщения – это его информационная характеристика.

Для расчёта энтропии целесообразнее всего воспользоваться приближённой формулой, которая является достаточно точной при большом числе уровней квантования:

, (9.1)

где W(x) – плотность вероятности сообщения;

h – значение интервала квантования;

Um – порог ограничения сообщения.

(9.2)

Для третьего распределения плотность вероятности сообщения (3.1):

W₃(x) =

Получаем:

H₃(x) = (9.3)

H₃(x) =

H₃(x)=10,114

10. Расчет избыточности и информационной насыщенности сообщения.

(10.1)

(10.1) – формула для расчета информационной насыщенности сообщения

где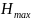 - максимальная энтропия источника, достигаемая при распределении равномерной плотности вероятности ;

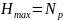= 0,843 (10.2)

Следовательно,R избыточность может быть найдена:

(10.3)

11.Расчет производительности источника сообщения и канала связи.

Производительность источника сообщения находится по формуле:

(11.1)

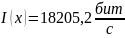
Расчет отношения сигнал – шум через формул Шеннона:

(11.2)

В равенствах (11.1) и (11.2) в качестве верхней частоты спектра сообщения принята частота f₀, так как такой прибор гарантирует некоррелированность отчетов сообщения х(t).

Следует иметь в виду, что в данном случае речь идёт о мощности шума в полосе частот, равной половине частоты дискретизации сообщения, и что при этом информация передаётся без искажений.

12. Выбор сложного сигнала для передачи информационного кода и синхронизации.

Достоинства сложных сигналов:

• Сложные сигналы обладают повышенной помехоустойчивостью по отношению к помехам с сосредоточенным спектром (узкополосным помехам);

• Так же сложные сигналы обладают повышенной разрешающей способностью, которая позволяет разделить сигналы при многолучевом распространении.

• Кроме того, использование сложного сигнала позволяет обеспечить синхронизацию устройства восстановления аналогового сообщения по принятому цифровому сигналу.

Нам необходимо выбрать два вида используемых сигналов с ОФМ. Один сигнал должен быть использован для синхронизации, второй – для передачи информационных символов.

Э

(12.1)

лемент последовательности рассчитывается по формуле:

гдес и d – двоичные числа.

Сформируем информационную последовательность из 15 символов. Формула (12.1) примет вид:

(12.2)

Начальное условие: d₁ = 0, d₂ = 0, d₃ = 1, d₄ = 1.

Мы получили информационную последовательность:

001101011110001

По этим данным строим структурную схему согласованного фильтра для синхроимпульса.

Рисунок 3. Структурная схема согласованного фильтра информационной последовательности

СФОИ – согласованный фильтр с еденичным импульсом.

Строим функцию корреляции для информационного импульса.

	1	0	0	0	1	1	1	1	0	1	0	1	1	0	0
*	0	1	1	1	0	0	0	0	1	0	1	0	0	1	1
*		0	1	1	1	0	0	0	0	1	0	1	0	0	1
			1	0	0	0	1	1	1	1	0	1	0	1	1
				1	0	0	0	1	1	1	1	0	1	0	1
*					0	1	1	1	0	0	0	0	1	0	1
						1	0	0	0	1	1	1	1	0	1
*							0	1	1	1	0	0	0	0	1
								1	0	0	0	1	1	1	1
									1	0	0	0	1	1	1
										1	0	0	0	1	1
											1	0	0	0	1
*												0	1	1	1
*													0	1	1
*														0	1
															1
Σ	-1	0	3	2	-3	-2	-3	2	1	2	-3	-4	-1	0	15

Рисунок 4. Функция корреляции информационной последовательности

Сформируем синхропоследовательность из 15 символов. Формула(

(12.3)

12.1) примет вид:

Начальное условие: d₁ = 0, d₂ = 0, d₃ = 1, d₄ = 1.

Мы получили информационную последовательность:

001111010110010

По этим данным строим структурную схему согласованного фильтра для синхроимпульса.

Рисунок 5. Структурная схема согласованного фильтра синхропоследовательности

Строим функцию корреляции для синхроимпульса.

	0	1	0	0	1	1	0	1	0	1	1	1	1	0	0
*	1	0	1	1	0	0	1	0	1	0	0	0	0	1	1
*		1	0	1	1	0	0	1	0	1	0	0	0	0	1
			0	1	0	0	1	1	0	1	0	1	1	1	1
				0	1	0	0	1	1	0	1	0	1	1	1
					0	1	0	0	1	1	0	1	0	1	1
						0	1	0	0	1	1	0	1	0	1
*							1	0	1	1	0	0	1	0	1
								0	1	0	0	1	1	0	1
*									1	0	1	1	0	0	1
										0	1	0	0	1	1
											0	1	0	0	1
*												1	0	1	1
*													1	0	1
														0	1
*															1
	1	0	-1	2	-1	-4	1	-2	3	0	-3	0	-1	-2	15

Рисунок 6. Функция корреляции синхропоследовательности

С

(12.4)

формируем чужую последовательность из 15 символов.

Начальное условие: d₁ = 0, d₂ = 0, d₃ = 1, d₄ = 1.

Строим функцию корреляции чужой последовательности для фильтра информационного импульса.

	1	0	0	1	1	1	0	1	0	0	1	1	1	0	0
*	0	1	1	0	0	0	1	0	1	1	0	0	0	1	1
*		0	1	1	0	0	0	1	0	1	1	0	0	0	1
			1	0	0	1	1	1	0	1	0	0	1	1	1
				1	0	0	1	1	1	0	1	0	0	1	1
*					0	1	1	0	0	0	1	0	1	1	0
						1	0	0	1	1	1	0	1	0	0
*							0	1	1	0	0	0	1	0	1
								1	0	0	1	1	1	0	1
									1	0	0	1	1	1	0
										1	0	0	1	1	1
											1	0	0	1	1
*												0	1	1	0
*													0	1	1
*														0	1
															1
	-1	0	3	0	-5	0	1	2	1	0	1	-8	3	4	7

Рисунок 7. Функция корреляции чужой последовательности для фильтра информационной последовательности

Строим функцию корреляции чужой последовательности для фильтра синхроимпульса.

	1	0	0	1	1	1	0	1	0	0	1	1	1	0	0
*	0	1	1	0	0	0	1	0	1	1	0	0	0	1	1
*		0	1	1	0	0	0	1	0	1	1	0	0	0	1
			1	0	0	1	1	1	0	1	0	0	1	1	1
				1	0	0	1	1	1	0	1	0	0	1	1
					1	0	0	1	1	1	0	1	0	0	1
						1	0	0	1	1	1	0	1	0	0
*							0	1	1	0	0	0	1	0	1
								1	0	0	1	1	1	0	1
*									0	1	1	0	0	0	1
										1	0	0	1	1	1
											1	0	0	1	1
*												0	1	1	0
*													0	1	1
														1	0
*															0
	-1	0	3	0	-3	-2	-1	4	1	4	1	-8	-1	2	7

Рисунок 8. Функция корреляции чужой последовательности для фильтра синхропоследовательности