6. Расчет допустимой вероятности ошибки, вызванной действием помех.
При оптимальном приёме оптимальный приёмник вычисляет апостериорную плотность распределения вероятности и выдаёт то значение сообщения, при котором апостериорная плотность максимальна.
Эффективное значение среднеквадратичной ошибки воспроизведения сообщения, вызванной ошибочным приемом одного из символов двоичного кода за счет широкополосного шума, можно найти по формуле:
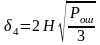, (6.1)
где
Рош –
вероятность ошибки приема разрядного
символа. Приведенная формула справедлива
при небольших значениях
.
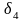Из формулы (6.1) выразим допустимую вероятность ошибки:
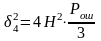(6.2)
отсюда выражаем
:
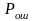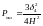(6.3)
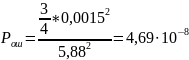
7. Ширина спектра.
В результате манипуляции двоичная
последовательность двоичных кодовых
импульсов с различными начальными
частотами может быть представлена
суммой двух импульсных последовательностей
с различными начальными частотами.
Спектральная плотность мощности такой
последовательности имеет вид
,
максимум которой находится на несущей
частоте, а ширина главного лепестка по
первым нулям спектральной плотности
.
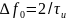(7.1)
На практике ширина спектра определяется полосой частот, в которой сосредоточено 80-90 % мощности сигнала.
При условии, что
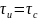(длительность
импульса и сигнала соответственно),
тогда
;
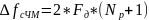(7.2)
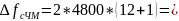124,8
кГц (7.3)
8. Расчет отношения мощностей сигнала и помехи, необходимых для обеспечения заданного качества приема.
Задаваясь значением вероятности
ошибки, можно найти требуемое значение
-
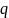отношение мощностей сигнал - шум
,
обеспечивающее качество приема при
наилучшем способе.
При когерентном приеме:
,
(8.1)
где - отношение мощностей сигнал - шум,
, (8.2)
где
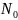-спектральная
плотность сигнала,
-
энергия сигнала. Таким образом,
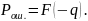(8.3)
(8.4)
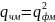(8.5)
Для нахождения вероятности ошибки используется формула:
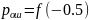(8.6)
Проведем аппроксимацию функции Лапласа:
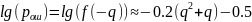(8.6a)
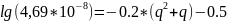
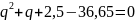
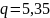
qфм = 5,35
Найдем отношение энергии сигнал шум в частотной модуляции когерентного приемника:
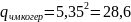
При некогерентном приёме:
Выражение для вероятностей ошибок зависят от конкретной схемы, реализующей различие символов двоичного кода дискретного сигнала. При рациональном построении устройств некогерентной обработки можно использовать приближённое выражение для вероятности ошибки при частотной модуляции:
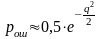(8.7)
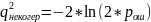(8.8)
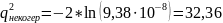
Получив значения отношения мощностей сигнал - шум при оптимальном и неоптимальном приеме, оценим проигрыш в энергии (мощности) сигнала, вызванной неизвестностью начальной фазы с помощью коэффициента проигрыша:
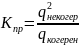(8.9)
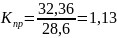
В результате получаем проигрыш энергии сигнала, который равен -13%.