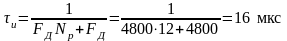2. Расчет частоты дискретизации.
По результатам распределения Относительной среднеквадратичной ошибки рассчитывается частота дискретизации (Fд).
По теореме Котельникова :
Fд=2Fв (2.1)
Эффективное значение относительной ошибки временной дискретизации сообщения x(t) определяется равенством:
δ1=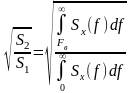
, (2.2)
где Fд – частота дискретизации;
Sx(f) – спектральная плотность мощности сообщения x(t);
S1 – площадь всей фигуры (Рисунок 1);
S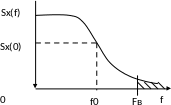
2
– площадь заштрихованной части (Рисунок
1).
Рисунок 1. Cпектральная плотность сигнала
В задании на проектирование форма спектральной плотности мощности сообщения определена равенством
Sx(f)=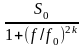
, (2.3)
где S0 – спектральная плотность мощности сообщения на нулевой частоте;
k – параметр, характеризующий порядок фильтра, формирующего сообщение;
f0 – частота, определяющая ширину спектра сообщения по критерию снижения Sx(f) в два раза по сравнению с её значением на нулевой частоте Sx(0).
,
(2.4)
где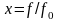
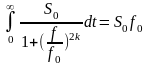(2.5)
(2.6)
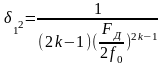(2.7)
Пользуясь формулой (2.7) можно вычислить частоту временной дискретизации Fд (Гц):
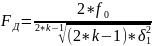
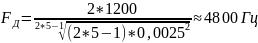
3. Расчет пикфактора.
Пикфактор - отношение максимального пикового значения непрерывного сообщения к его эффективному значению:
Определение пикфактора использует четыре вида законов распределения аналоговых сообщений. В нашем случае закон четвертого вида сообщения.
3 3,5 4 4,5 5 5,5 6 Н
2
10-1
10-2
10-3
10-4
10-5
Рисунок 2. График зависимости эффективного значения относительной ошибки от пикфактора.
Сообщение четвертого вида имеет распределение:
W4(x)
=
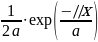(3.1)
Дисперсия такого процесса равна:
x2=2a2х (3.2)
Н=4,16
следовательно, пикфактор этого сообщения
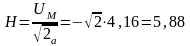
4. Расчет числа Np двоичного кода.
Связь эффективного значения относительной ошибки квантования δ1 с числом разрядов Np двоичного кода при достаточно высоком числе уровней квантования, когда ошибку можно считать распределенной по закону равномерной плотности, определяется выражением:
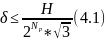
Таким образом, задавшись допустимым значением относительной ошибки δ3, можно найти число разрядов двоичного кода, обеспечивающее заданную точность преобразования:
Np=
E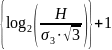
,
(4.2)
где E – целая часть дробного числа x.
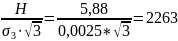
Np=
E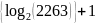
=12
разрядов.
В результате получили, что наш приемник сможет передавать 12 разрядный двоичный код.
5. Расчёт длительности импульса двоичного кода
После определения частоты дискретизации и числа разрядов двоичного кода можно определить длительность импульса кодовой последовательности:
,
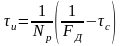(5.1)
где с – длительность временного интервала, предназначенного для передачи сигналов синхронизации.
Приведенная формула справедлива для АМ, ЧМ и ФМ во второй ступени модуляции системы.
Пусть
,
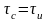тогда после преобразований мы получаем
формулу для длительности импульса:
