Основные сведения о матрицах

Матрицей размера называется прямоугольная таблица чисел, содержащая т строк и п столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Для обозначения матриц используются прописные латинские буквы, например, А, В, С, ..., а для обозначения их элементов - соответствующие строчные буквы с двойной индексацией: , где i - номер строки, j - номер столбца.

Общий вид матрицы размерности следующий:

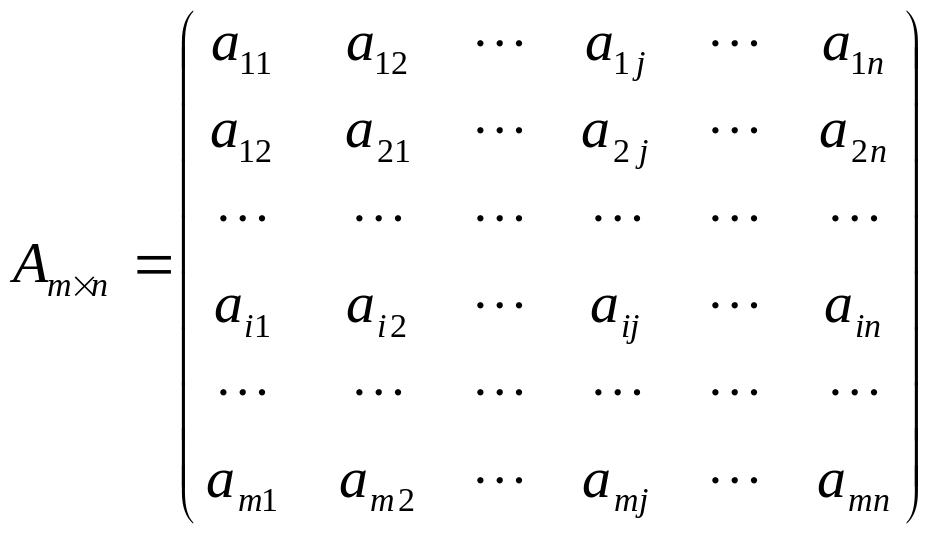(1)

или, в сокращенной записи, ; ;

Например,

.

Наряду с круглыми скобками используются и другие обозначения матрицы: , .

Две матрицы A и В одинаковой размерности называются равными, если они совпадают поэлементно, т.е. для любых ;

Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой, а из одного столбца - матрицей (вектором)-столбцом: - матрица-строка;

.

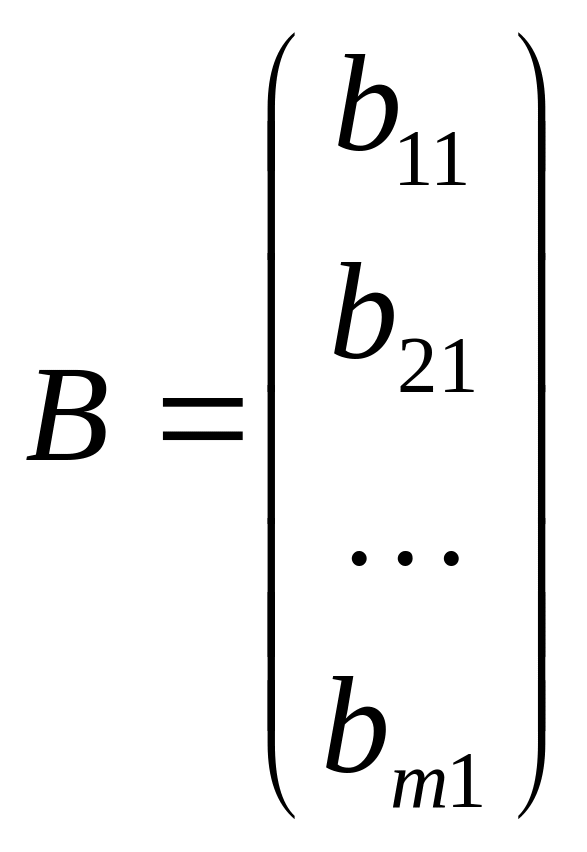Определение. Матрица называется квадратной n-го порядка ( ), если число ее строк равно числу столбцов и равно п.

Элементы матрицы , у которых номер столбца равен номеру строки (i=j), называются диагональными и образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы , , …, .

Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.

Если у диагональной матрицы n-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n-го порядка, она обозначается .

Матрица любого размера называется нулевой, если все ее элементы равны нулю:

Операции над матрицами

1. Умножение матрицы на число.

Произведением матрицы на число называется матрица , каждый элемент которой равен произведению соответствующего элемента матрицы на число , т.е. для ; .

Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.

В частности, произведение матрицы А на число 0 есть нулевая матрица, т.е .

2. Сложение матриц.

Суммой двух матриц и одинакового размера называется матрица , каждый элемент которой равен сумме соответствующих элементов матриц и , т.е. для ; (т.е. матрицы складываются поэлементно).

3. Вычитание матриц.

Разность двух матриц одинакового размера определяется через предыдущие операции: .

4. Умножение матриц.

Произведение матриц и определено, когда число столбцов матрицы равно числу матрицы . Произведением матриц называется такая матрица , каждый элемент которой равен сумме произведений элементов -й строки матрицы на соответствующие элементы -го столбца матрицы : , ; .

(Иными словами, матрицы умножаются строка на столбец).

Операции над матрицами обладают следующими свойствами:

1) ;

2) ;

3) .

4) ;

5) ;

6) ;

7) .

Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:

а) Если произведение матриц существует, то после перестановки сомножителей местами произведения матриц может и не существовать.

б) Если даже произведения и существуют, то они могут быть матрицами разных размеров.

в) В случае, когда оба произведения и существуют и оба - матрицы одинакового размера (это возможно только при умножении квадратных матриц и одного порядка), коммутативный (переместительный) закон умножения, вообще говоря, не выполняется, т.е. .

В частном случае коммутативным законом обладает произведение любой квадратной матрицы -го порядка на единичную матрицу того же порядка, причем это произведение равно :

Таким образом, единичная матрица играет при умножении матриц ту же роль, что и число 1 при умножении чисел.

г) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что , не следует, что или .

5. Возведение в степень. Целой положительной степенью квадратной матрицы называется произведение матриц, равных , т.е.

.

Заметим, что операция возведения в степень определена только для квадратных матриц. Полагают , . Нетрудно показать, что , . Если , то это не означает, что матрица .

6. Транспонирование матрицы - переход от матрицы к матрице , в которой строки и столбцы поменяны местами с сохранением порядка. Матрица называется транспонированной относительно матрицы :

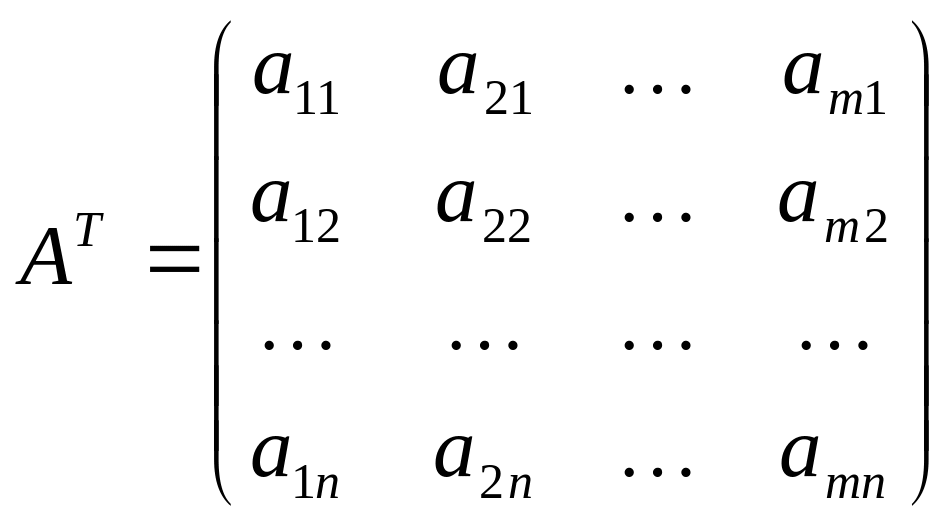, . (2)

Из определения следует, что если матрица имеет размер , то транспонированная матрица имеет размер .

Свойства операции транспонирования:

1)

2)

3)

4) .