3 Гипербола
К
ривая
второго порядка (13) называется гиперболой
(кривой гиперболического типа),
если коэффициенты
и
имеют противоположные знаки, т.е.
.
Пусть для определенности
,
.
Возможны три случая.
1) соответствует гиперболе с каноническим уравнением вида
,
(15)
где
– действительная
полуось,
а
– мнимая
полуось.
Фокусы
гиперболы
– точки
и
,
где
,
а ее эксцентриситет
принимает любые значения, большие
единицы. Вершины гиперболы – точки
и
.
Можно показать, что для любой точки
гиперболы абсолютная величина разности
ее расстояний до фокусов есть величина
постоянная, равная
:
.
Это характеристическое
свойство гиперболы
часто принимают за определение гиперболы.
Прямые
,
называется асимптотами
гиперболы.
Для равносторонней гиперболы (
)
асимптоты
взаимно перпендикулярны и представляют
биссектрисы координатных углов.
2)
При
уравнение кривой (15) примет вид
,
т.е. получим пару пересекающихся прямых
и
.
3)
При
получим гиперболу
с полуосями
- и
,
называемую сопряженной с гиперболой
(15) (на рисунке она изображена пунктиром).
4 Парабола
Пусть
в уравнении кривой второго порядка (10)
,
а также один из коэффициентов
или
равен нулю. Пусть для определенности
,
,
тогда
. (16)
Или,
после выделения полного квадрата при
y:
.
Полагая
,
,
,
получим
.
(17)
К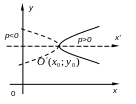
ривая
(17) называется параболой,
точка
– вершиной
параболы,
p
– параметром
параболы.
При
ветви параболы направлены вправо, при
- влево. Прямая
является осью симметрии параболы.
Если вершина параболы находится в начале координат, то уравнение (17) принимает вид:
.
(18)
Точка
называется фокусом
параболы, а прямая
- ее директрисой.
М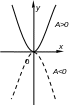
ожно
показать, что парабола представляет
множество всех точек плоскости,
равноотстоящих от данной точки (фокуса)
и от данной прямой (директрисы). Это
характеристической
свойство параболы
часто принимается за определение
параболы.
Если
в уравнении (18) поменять местами
и
,
то получим
- уравнение параболы с вершиной в начале
координат, симметричной относительно
оси ординат. Это уравнение обычно
записывают в виде
,
где
.
При
ветви параболы направлены вверх, при
- вниз.
Можно
показать, что , график квадратного
трехчлена
есть парабола с вершиной в точке
и осью симметрии
,
параллельной оси
.