9 Угол между прямыми

Р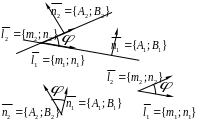 ассмотрим две прямые, заданные общими уравнениями и . Можно показать, что угол между прямыми (т.е. их направляющими векторами и ) и угол между их нормалями и равны, тогда из свойств скалярного произведения векторов нормалей найдем: .

Кроме того, если прямые заданы уравнениями с угловым коэффициентом, т.е. , , то угол между ними можно определить как .

10 Условия параллельности и перпендикулярности прямых

а) Если прямые и параллельны, то угол между ними , , откуда .

б) Если прямые, заданные общими уравнениями и , параллельны, то их нормальные вектора и также параллельны, а их координаты пропорциональны. Тогда условие параллельности прямых, заданных общими уравнениями, формулируется как .

в) Если прямые и перпендикулярны, то угол между ними , , откуда и .

г) Если прямые, заданные общими уравнениями и , перпендикулярны, то их нормальные вектора и также перпендикулярны, а их скалярное произведение равно нулю. Тогда условие перпендикулярности прямых, заданных общими уравнениями, формулируется как .

11 Точка пересечения прямых.

Пусть даны две прямые и . Очевидно, что координаты их точки пересечения должны удовлетворять уравнению каждой прямой, т.е. они могут быть найдены из системы

.

Е сли прямые не параллельны, т.е. , то решение системы дает единственную точку пересечения прямых.

12 Расстояние от точки до прямой.

Пусть даны точка и прямая . Под расстоянием от точки до прямой понимается длина перпендикуляра , опущенного из точки на прямую . Можно показать, что его величина определяется по формуле .

Кривые второго порядка на плоскости

1 Окружность

У равнение окружности радиуса с центром имеет вид

. (9)

В частности, уравнение окружности с центром в начале координат имеет вид .

Рассмотрим уравнение второй степени с двумя переменными в общем виде

, (10)

в котором , и не равны нулю одновременно, т.е. .

Чтобы уравнения (9) и (10) представляют одну и ту же линию, коэффициент должен равняться нулю, т.е. , а все остальные коэффициенты – быть пропорциональны, в частности, , откуда (т.к. , а ). Тогда получим уравнение

, (11)

называемое общим уравнением окружности.

Поделив обе части уравнения на и дополнив члены, содержащие и , до полного квадрата, получим

. (12)

Сравнивая уравнения (12) и (9), можно сделать вывод что уравнение (12) есть уравнение действительной окружности, если 1) ; 2) ; 3) . При выполнении этих условий центр окружности (12) расположен в точке , а ее радиус .

2 Эллипс

Перепишем (10) в виде или , где ; ; . В предположении уравнение кривой примет вид:

. (13)

Кривая второго порядка (13) называется эллипсом (кривой эллиптического типа), если коэффициенты и имеют одинаковые знаки. Будем считать, что и (в противном случае обе части уравнения можно умножить на ( )). Тогда возможны три случая:

1) – кривая (13) не имеет действительных точек;

2) – кривая (13) представляет собой одну точку;

3) – кривая (13) переписывается в виде

. (14)

У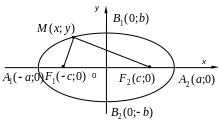 равнение (14) называется каноническим уравнением эллипса с полуосями и . При уравнение (14) представляет собой уравнение окружности . В предположении, что a>b, обозначим , тогда точки и называются фокусами эллипса, а отношение – его эксцентриситетом. Эксцентриситет характеризует форму эллипса. Очевидно, что , причем для окружности .

Можно показать, что для любой точки эллипса сумма расстояний от этой точки до фокусов есть величина постоянная, равная . Это характеристической свойство эллипса часто принимается за его определение.