Элементы аналитической геометрии на плоскости Декартова система координат на плоскости. Уравнение линии
Для
задания декартовой системы координат
на плоскости определяют точку О
– начало координат, пару неколлинеарных
векторов, образующих базис, и единицу
измерения длины. Прямые, проведенные
через начало координат параллельно и
сонаправленно базисным векторам,
называют осями координат. Если оси
перпендикулярны, то система координат
называется прямоугольной. С горизонтальной
осью абсцисс Ox
и вертикальной осью ординат Oy.
Ортонормированный базис на плоскости
принято обозначать векторами
для оси абсцисс и
для оси ординат. Тогда координатами
точки M
на плоскости Oxy
будут проекции ее радиус-вектора
на соответствующие оси.
Если
,
,
то для определения координат точки
,
делящей отрезок в заданном соотношении
,
используются формулы
,
.
Расстояние между точками A
и B
определяется как
.
Уравнением
линии (кривой)
на плоскости
называется уравнение, которому
удовлетворяют координаты
и
каждой точки данной линии и не удовлетворяют
координаты любой точки, не лежащей на
этой линии.
В
общем случае уравнение линии может быть
записано в неявном виде
или в явном виде
,
где
и
– некоторые функции.
Чтобы
убедиться, что точка
лежит на данной линии
,
надо проверить, обращают ли координаты
этой точки уравнение
в верное равенство.
Прямая на плоскости
1 Уравнение прямой с угловым коэффициентом
П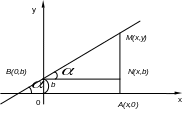
усть
прямая пересекает ось Oy
в точке
и образует с осью Ox
угол
(
).
Возьмем
на прямой произвольную точку
.
Тогда тангенс угла
наклона прямой найдем из прямоугольного
треугольника
:
.
Введем
угловой коэффициент прямой
,
откуда получим уравнение
прямой с угловым коэффициентом
(1)
1.
Если
,
то получаем
– уравнение прямой, проходящей через
начало координат и образующей при
острый угол с осью Ox,
а при
– тупой угол.
2.
Если
,
то
,
и уравнение прямой, параллельной оси
Ox,
имеет вид
,
а самой оси Oy
– вид
.
3.
Если
,
то прямая перпендикулярна оси Ox
и
не существует, т.е. прямая не имеет
углового коэффициента, т.е. вертикальна
и параллельна оси Oy.
Предположим, что эта прямая отсекает
на оси Ox
отрезок, равный a.
Очевидно, что уравнение такой прямой
,
т.к. абсцисса любой точки прямой равна
,
а уравнение оси Oy
есть
.
2 Уравнение прямой, проходящей через данную точку в данном направлении (с заданным угловым коэффициентом)
Пусть
прямая проходит через точку
и образует с осью Ox
угол
.
Т.к. точка
лежит на прямой, то ее координаты
удовлетворяют уравнению (1), т.е.
.
Вычитая его из равенства (1), получим уравнение искомой прямой
. (2)
3 Уравнение прямой, проходящей через заданную точку с направляющим вектором
Пусть
прямая проходит через точку
параллельно вектору
.
Рассмотрим произвольную точку прямой
M(x;y).
Поскольку искомая прямая и вектор
параллельны то векторы
={x–x1;y–y1}
и
также параллельны, а их координаты
пропорциональны, т.е.
(3)
Уравнение (3) и называется уравнением прямой, проходящей через заданную точку M с направляющим вектором .
4 Параметрическое уравнение прямой
Обозначим
коэффициент пропорциональности координат
в уравнении (3) t,
т.е.
.
Тогда
,
,
откуда параметрическое
уравнение прямой
(4)
5 Уравнение прямой, проходящей через две заданные точки.
Пусть
даны две точки
,
и
,
.
Тогда направляющий вектор прямой
в координатах определяется как
,
а уравнение
прямой, проходящей через две заданные
точки
определяется подстановкой его координат
в (3), т.е.
. (5)
6 Уравнение прямой в отрезках.
Найдем
уравнение прямой по заданным отрезкам
и
,
отсекаемым на осях координат. Используя
уравнение прямой, проходящей через
точки
и
(5) получим:
.
После преобразования получим уравнение
прямой в отрезках или каноническое
уравнение прямой
. (6)
7 Уравнение прямой с нормальным вектором
Пусть
прямая проходит через точку
перпендикулярно ненулевому вектору
(
).
Тогда произвольный направляющий вектор
прямой
={x–x1;y–y1}
перпендикулярен вектору
,
а их скалярное произведение равно нулю,
т.е.
. (7)
Уравнение (7) и называется уравнением прямой с нормальным вектором, а вектор – нормалью данной прямой.
8 Общее уравнение прямой и его исследование.
Уравнение (7) можно записать в виде
, (8)
где
.
Форму (8) называют общим уравнением
прямой на плоскости.
1)
Пусть
,
,
,
тогда уравнение (8) можно записать в виде
– уравнение прямой с угловым коэффициентом,
не проходящей через начало координат.
2)
Пусть
,
,
,
тогда уравнение (8) можно записать в виде
– уравнение прямой с угловым коэффициентом,
проходящей через начало координат.
3)
Пусть
,
,
,
тогда (8) имеет вид
,
– прямая, параллельная оси Oy.
4)
Пусть
,
,
,
тогда (8) имеет вид
,
– ось Oy.
5)
Пусть
,
,
,
тогда уравнение (8) можно записать в виде
,
–прямая, параллельная оси Ox.
6)
Пусть
,
,
,
тогда уравнение (8) можно записать в виде
,
– ось Ox.
Отметим, что коэффициенты A и B есть координаты вектора нормали данной прямой.