Задача 4

Вертикальный цилиндрический резервуар высотой H и диаметром D закрывается полусферической крышкой, сообщающейся с атмосферой через трубу внутренним диаметром d (рис.4.1). Резервуар заполнен мазутом, плотность которого ρ = 900 кг/м³.

Рис.4.1

Требуется определить:

1. Высоту поднятия мазута h в трубе при повышении температуры на t°С.

2. Усилие, отрывающее крышку резервуара при подъёме мазута на высоту h за счет его разогрева.

Коэффициент температурного расширения мазута принять равным β_t = 0,00072 1/°С.

Дано: D = 2,2 м,

H = 2,2 м,

d = 125 мм = 0,125 м,

t = 15 °С,

β_t = 0,00072 1/°С,

ρ = 900 кг/м³

Найти: h = ? Р_z = ?

Решение.

Определим объём резервуара, состоящий из цилиндрической и полусферической частей. Это будет первоначальный объём мазута.

Используя формулу коэффициента температурного расширения β_t, найдем приращение этого объёма за счёт его расширения при нагреве на t°С.

,

где Δt = t°C – приращение температуры.

Поделив найденное приращение объёма ΔW на площадь поперечного сечения трубы, получим искомую высоту поднятия мазута h:

Для нахождения усилия, отрывающего крышку резервуара от плоскости разъёма, необходимо найти объём тела давления W (объём, ограниченный горизонтальной плоскостью, проведённой по свободной поверхности мазута в трубе, и полусферической крышкой). Этот объём будет состоять из объёма цилиндра диаметром D и высотой (D+h) минус объём полусферы диаметром D и объём малого цилиндра диаметром d и высотой h (на рис.4.1.1 заштриховано)

Рис. 4.1.1

Искомое усилие определится по формуле:

Ответ: h = 9,8 м, Р_z = 339,917 кН

Задача 5

К системе, состоящей из двух параллельно соединённых трубопроводов, имеющих длины соответственно l₁ и l₂ и диаметры d₁ и d₂ (коэффициент шероховатости n = 0,012), подводится к точке A вода, расход которой Q (рис.5.1).

Рис.5.1

Требуется определить потерю напора на участке AA₁ и величины расходов воды на каждом участке.

Дано: n = 0,012,

Q = 69 л/с = 0,069 м³/с,

l₁ = 500 м, d₁ = 200 мм = 0,2 м,

l₂ = 550 м, d₂ = 200 мм = 0,2 м

Найти: h_l = ? Q_1,2 = ?

Решение.

Потери напора на каждом из двух параллельно соединённых трубопроводов будут одинаковы:

h_l1 = h_l2 = h_l

где h_l1 и h_l2 – потери напора по длине соответственно на первом и втором трубопроводах.

1. Определим модули расхода для первого и второго трубопровода по формуле:

где ω – площадь живого сечения;

С – коэффициент Шези;

R =ω/χ – гидравлический радиус;

χ – смоченный периметр.

В случае напорного трубопровода χ = πd.

Коэффициент Шези определяется по формуле Маннинга:

где n – коэффициент шероховатости.

Площадь живого сечения:

Гидравлический радиус:

Коэффициент Шези:

Модуль расхода:

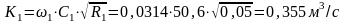
2. Вычислим потерю напора на участке AA₁ по формуле:

3. Определим расходы в каждом из трубопроводов:

Ответ: h_l = 4,95 м, Q₁ = 35 л/с, Q₂ = 34 л/с

Задача 6

Поршень диаметром D имеет n отверстий диаметром d₀ каждое (рис.6.1). Отверстия рассматривать как внешние цилиндрические насадки с коэффициентом расхода μ = 0,82; плотность жидкости ρ = 900 кг/м³.

Требуется определить скорость v перемещения поршня вниз, если к его штоку приложена сила F.

Рис.6.1

Дано: D = 100 мм = 0,1 м,

d₀ = 12 мм = 0,012 м,

n = 4,

F = 8 кН = 8000 Н

Найти: v = ?

Решение.

Определим величину давления под поршнем p, определяемую силой, приложенной к поршню, и площадью поршня за вычетом суммарной площади отверстий:

Расход жидкости из каждого отверстия (насадка) определим по формуле:

где μ – коэффициент расхода;

ω₁ – площадь одного отверстия;

ρ – плотность жидкости.

Суммарный расход:

Скорость перемещения поршня вниз:

где S_D – площадь поперечного сечения поршня

Ответ: v = 2,3 м/с