1.2. Вторая задача
Необходимо так распределить задачи между узлами , чтобы обеспечить минимум общих затрат ( критерий 1) или минимум общего времени решения (критерий 2) при выполнении ограничений на общее время решения (9) или общие затраты (6) соответственно.
Математическая модель этой задачи может быть записана следующим образом:
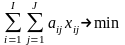(15)
при следующих ограничениях:
(16)
(17)
В соотношениях (15) - (17) приняты следующие обозначения:
- затраты (время решения) задачи , расположенной в узле ,
-
время решения (затраты) на задачу
,
расположенную в узле
,
-
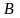общее время решения (затраты) всех
задач.
Для
решения этой задачи, прежде всего,
берутся минимальные элементы в каждой
строке матрицы коэффициентов
и проверяется выполнение условия (16)
для соответствующих элементов матрицы
коэффициентов
Если
условие (16) выполняется, то это и будет
оптимальным решением. Если оно не
выполняется, то из матрицы коэффициентов
и
исключают те элементы, которые не могут
войти ни в одно допустимое решение. Для
этого последовательно рассматриваются
все элементы матрицы
и проверяют следующее условие:
(18)
где
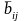- минимальный элемент в соответствующей
строке;
-
рассматриваемый элемент,
.
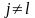Другими словами, каждая задача последовательно закрепляется за каждым из узлов и проверяется выполнение условия (16) в лучшем случае.
Если условие (18) нарушается, то соответствующий элемент не входит в допустимое решение и исключается из матрицы . Из матрицы исключается соответствующий элемент .
Из
условия (17) следует, что в каждой строке
может быть только один элемент. Поэтому
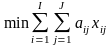без учета выражения (14) равен
.
Отсюда следует, что если для элементов
одновременно выполняются условия
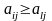и
,
,
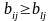то эти элементы могут быть исключены
из рассмотрения.
Хотя исключение элементов не всегда приводит к оптимальному решению, однако объем вычислений резко сокращается.
Далее используется метод «ветвей и границ». В отличие от предыдущей задачи, ветвление осуществляется с учетом ограничения (16), что существенно сокращает число рассматриваемых вариантов. Оценка для каждой вершины находится по элементам матрицы (15) аналогично предыдущей задаче (14). Ограничение при этом имеет следующий вид:
,
(19)
где
-
уровень ветвления;
.
Рассмотрим числовое решение второй частной задачи, а именно задачи минимизации общих затрат при ограничении на общее время решения всех задач, т.е. будем искать
(30)
при следующих ограничениях:
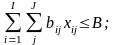(31)
(32)
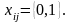(33)
Пусть
Сначала
находим минимальные элементы в каждой
строке матрицы
и проверяем, удовлетворяется ли условие
(31) по одноименным элементам матрицы
.
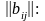
Условие (31) не выполняется, и задачу «в лоб» решить не удается. Приступим к упрощению матриц коэффициентов и . Для матрицы последовательно для всех элементов проверяется условие (18), т.е. условие
(34)
где - минимальный элемент в соответствующей строке;
- рассматриваемый элемент, .
Для
Элемент
не удовлетворяет условию (34), он исключается
из матрицы
,
и одноименный элемент
исключается из матрицы
.
Аналогично для
имеем:
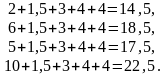
Для
Для
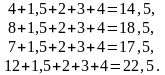
Для
:
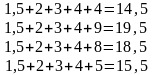
Легко
видно, что для
все элементы удовлетворяют условию
(34).
Поскольку
в каждой строчке может быть только один
элемент и в обеих матрицах
и
осуществляется
минимизации, то, очевидно, что при
одновременном выполнении условий
,
соответствующие элементы в матрицах
и
могут быть исключены из рассмотрения
одновременно.
Например, рассматривая первую строку в матрицах и , можно сделать следующее заключение, рассматривая следующие пары элементов этой строки:
-
(3 и 7) и (1,5 и 3) – условие
выполняется и, следовательно, можно
убрать элементы
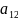и
;
-
(2 и 4) и (2 и 9) - условие
снова выполняется и, следовательно,
можно убрать элементы
и
.
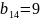Таким образом, первая строка матрицы запишется как ( 3 – 2 - ), а последняя строка как ( 7 - - 1).
После соответствующих упрощений матрицы и принимают следующий вид:
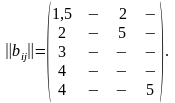
Из матрицы в каждой строке выбираем минимальные элементы и получаем следующее решение:
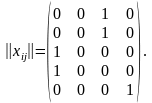
Подсчитываем время решения: 2+5+3+4+5=19<20. Оно не превышает допустимой величины. Задача решена.