
- •Оглавление
- •2.1. Краткие сведения из курса механики 12
- •2.2. Пример решения задания 14
- •3.1. Краткие сведения из курса механики 19
- •4.1. Краткие сведения из курса механики 30
- •4.2. Примеры решения заданий 35
- •Введение
- •Задание 1. Применение метода кинетостатики для определения усилий в связях механической системы
- •1.1. Краткие сведения из курса механики Метод кинетостатики
- •1.2. Пример решения задания
- •Задание 2. Определение опорных реакций на оси вращающегося тела
- •2.1. Краткие сведения из курса механики Динамические реакции связей
- •2.2. Пример решения задания
- •Задание 3. Расчет параметров движения (равновесия) тел механической системы при учете сухого трения и (или) трения качения
- •3.1. Краткие сведения из курса механики
- •3.1.1. Принцип возможных перемещений
- •3.1.2. Общее уравнение динамики
- •3.1.3. Уравнения Лагранжа второго рода
- •3.2. Примеры решения заданий Пример 3.2.1. Применение принципа возможных перемещений
- •Пример 3.2.2. Применение общего уравнения динамики
- •Пример 3.2.3. Применение уравнения Лагранжа 2-го рода
- •Задание 4. Расчет параметров движения (равновесия) тел механической системы, содержащей внешние и внутренние упругие связи, при учете линейно-вязкого сопротивления
- •4.1. Краткие сведения из курса механики
- •4.1.1. Свободные колебания линейных механических систем с одной степенью свободы.
- •4.1.2. Свободные колебания линейных механических систем с двумя степенями свободы.
- •4.2. Примеры решения заданий
- •4.2.1. Положение равновесия линейной механической системы с одной степенью свободы
- •4.2.2. Дифференциальное уравнение движения механической системы с одной степенью свободы
- •4.2.3. Равновесие линейной механической системы с двумя степенями свободы
- •4.2.4. Свободные колебания линейной механической системы с двумя степенями свободы
- •Список литературы
4.2.3. Равновесие линейной механической системы с двумя степенями свободы
Механическая
система, состоящая из однородного диска,
двух соосных (насаженных неподвижно на
единую ось) блоков и груза, прикрепленного
к земле пружиной (см. Рис. 9), находится
в положении статического равновесия.
Зная жесткости пружин
![]() и
и
![]() ,
веса грузов и радиусы блоков, определить
удлинения пружин в положении равновесия.
,
веса грузов и радиусы блоков, определить
удлинения пружин в положении равновесия.

Рис. 9
РЕШЕНИЕ
Рассматриваемая механическая система обладает двумя степенями свободы.
В качестве независимых обобщенных координат выберем линейные перемещения груза и центра диска
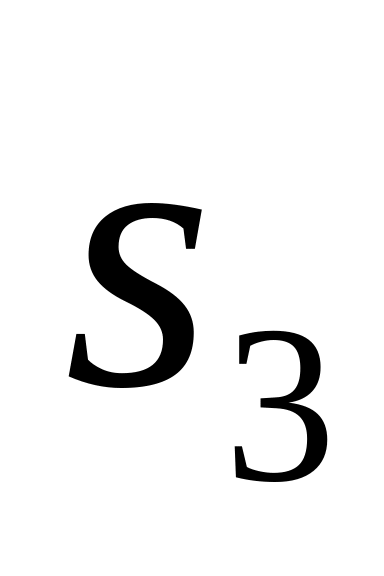 .
Заменим действие первой пружины силой
упругости
.
Заменим действие первой пружины силой
упругости
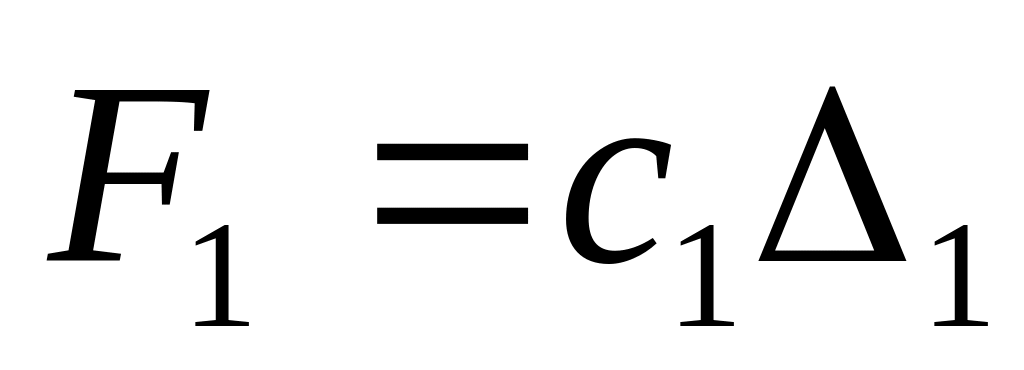 ,
где
,
где
 - удлинение пружины в положении
статического равновесия механической
системы, а второй - внутренней силой
- удлинение пружины в положении
статического равновесия механической
системы, а второй - внутренней силой
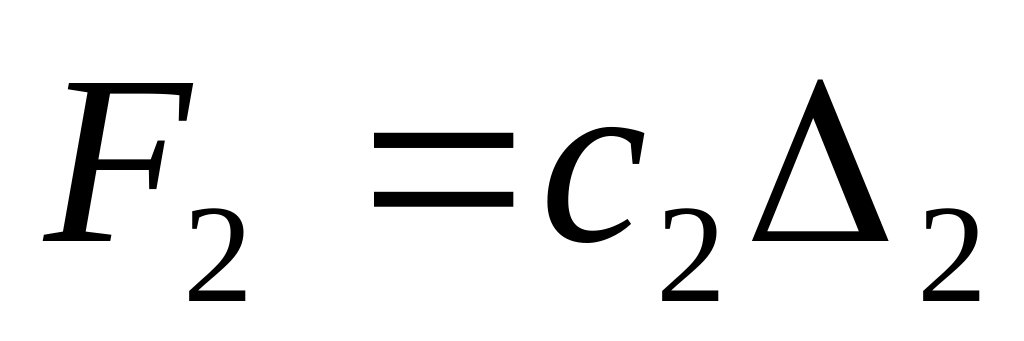 ,
где
,
где
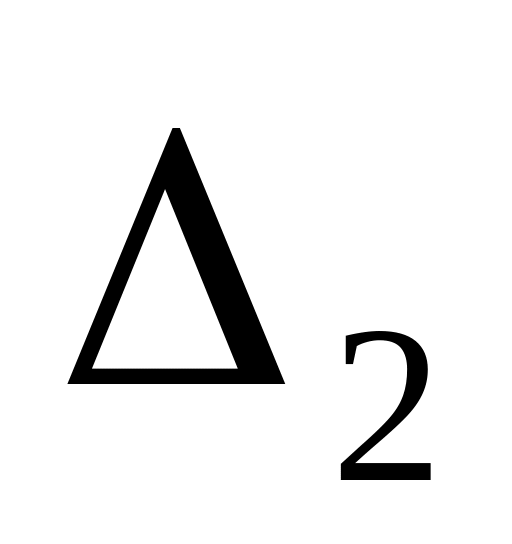 -
удлинение второй пружины.
-
удлинение второй пружины.Дадим системе возможное перемещение по первой обобщенной координате, положив равным нулю возможное перемещение по второй обобщенной координате (т.е.
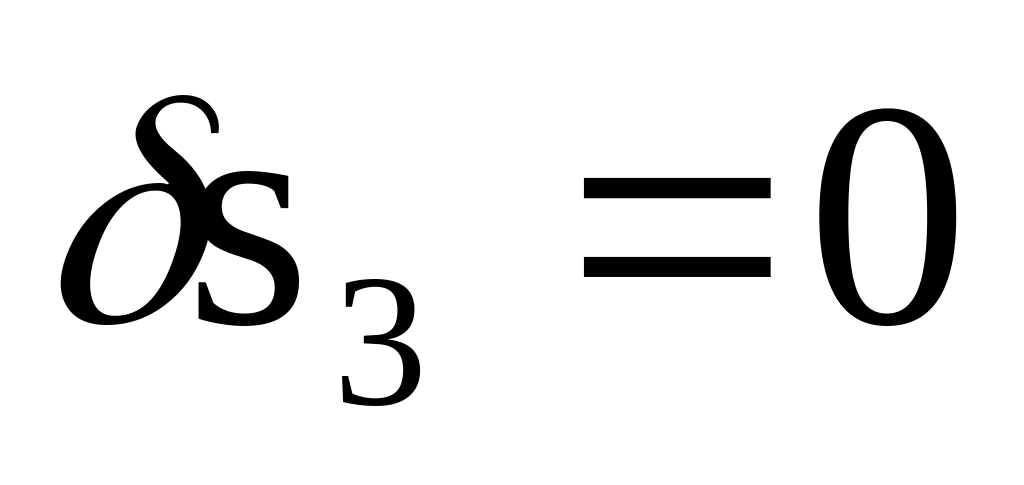 ).
Запишем для этого случая выражение
суммы работ всех действующих на систему
сил и приравняем ее к нулю (так как диск
остается неподвижным, действующие на
него силы работу не совершают). Вынесем
за общую скобку. Тогда
).
Запишем для этого случая выражение
суммы работ всех действующих на систему
сил и приравняем ее к нулю (так как диск
остается неподвижным, действующие на
него силы работу не совершают). Вынесем
за общую скобку. Тогда
![]() ,
,
где
![]() –
возможное перемещение в точке приложения
силы
–
возможное перемещение в точке приложения
силы
![]() .
.
Запишем уравнения связей, используя соотношения кинематики:
;
![]() .
.
Для рассматриваемой механической системы возможные перемещения пропорциональны соответствующим скоростям, т.е. справедливы соотношения
;
![]() .
.
Приравняв нулю выражение в круглых скобках, получим первое уравнение для расчета статического удлинения пружин:
![]() .
.
Теперь дадим системе возможное перемещение
 по
второй обобщенной координате, положив
равным нулю возможное перемещение по
первой обобщенной координате (т.е.
по
второй обобщенной координате, положив
равным нулю возможное перемещение по
первой обобщенной координате (т.е.
 ).
Запишем для этого случая выражение
суммы работ всех действующих на систему
сил и приравняем ее к нулю (так как груз
и соосный блок остаются неподвижными,
действующие на них силы работу не
совершают). Вынесем
за общую скобку. Тогда
).
Запишем для этого случая выражение
суммы работ всех действующих на систему
сил и приравняем ее к нулю (так как груз
и соосный блок остаются неподвижными,
действующие на них силы работу не
совершают). Вынесем
за общую скобку. Тогда
![]() ,
,
где
-
возможное перемещение в точке приложения
силы
![]() .
.
Запишем уравнения связей, используя соотношения кинематики:
;
![]() .
.
Для рассматриваемой механической системы возможные перемещения пропорциональны соответствующим скоростям, т.е. справедливо соотношение
![]() .
.
Приравняв нулю выражение в круглых скобках, получим второе уравнение для расчета статического удлинения пружин:
![]() .
.
Решив систему алгебраических уравнений относительно удлинений пружин, получим
![]() ;
;
![]() .
.
4.2.4. Свободные колебания линейной механической системы с двумя степенями свободы
Для механической
системы, изображенной на Рис. 9, получить
дифференциальные уравнения движения,
воспользовавшись уравнениями Лагранжа
второго рода. Составить выражения для
вычисления частот и форм главных
колебаний. Осевой момент инерции соосных
блоков
![]() полагать заданным.
полагать заданным.
РЕШЕНИЕ
Рассматриваемая механическая система обладает двумя степенями свободы.
В качестве независимых обобщенных координат выберем линейные перемещения груза и центра диска . Заменим действие первой пружины силой упругости
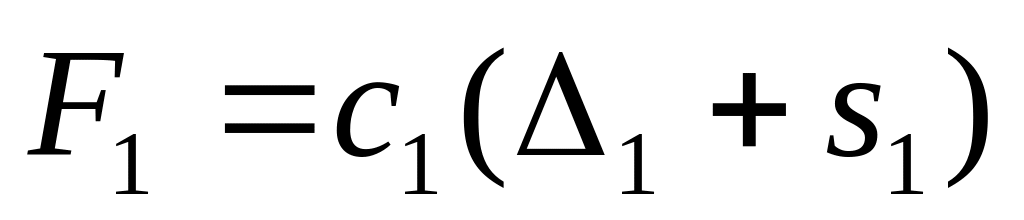 ,
где
- удлинение пружины в положении
статического равновесия механической
системы, а второй - внутренней силой
,
где
- удлинение пружины в положении
статического равновесия механической
системы, а второй - внутренней силой
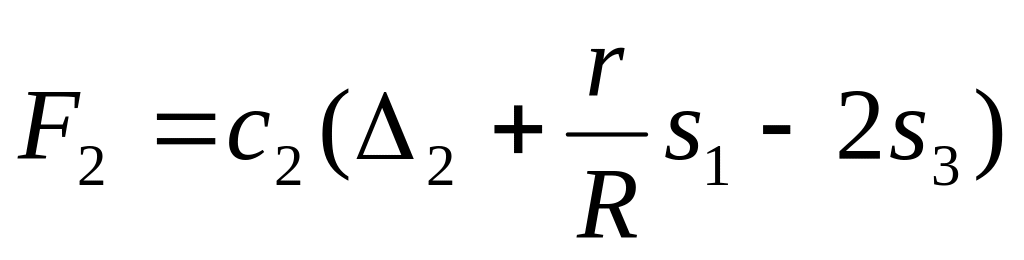 ,
где
-
удлинение второй пружины, а
,
где
-
удлинение второй пружины, а
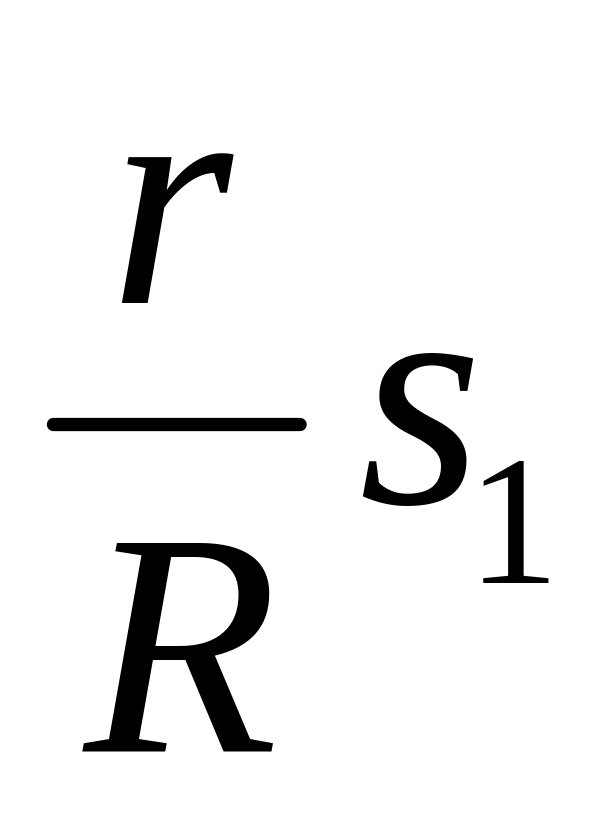 и
и
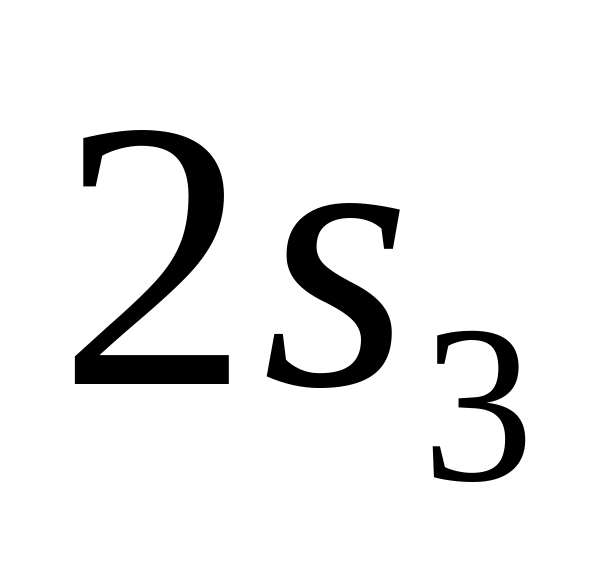 -
перемещения левого и правого концов
второй пружины, выраженные через
выбранные обобщенные координаты (см.
уравнения кинематических связей).
-
перемещения левого и правого концов
второй пружины, выраженные через
выбранные обобщенные координаты (см.
уравнения кинематических связей).Для составления уравнений Лагранжа второго рода (9) сначала получим выражения для обобщенных сил, воспользовавшись следующей формулой
 .
.Дадим системе возможное перемещение по первой обобщенной координате, положив равным нулю возможное перемещение по второй обобщенной координате (т.е. ). Запишем для этого случая выражение суммы работ всех действующих на систему сил (так как диск остается неподвижным, действующие на него силы работу не совершают). Вынесем за общую скобку. Тогда
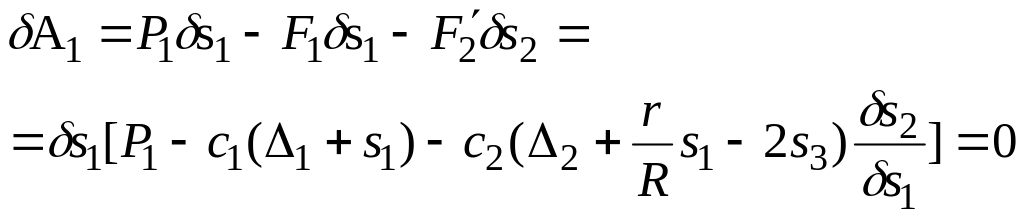 ,
,
где - возможное перемещение в точке приложения силы .
Запишем уравнения связей, используя соотношения кинематики:
;
.
Для рассматриваемой механической системы возможные перемещения пропорциональны соответствующим скоростям, т.е. справедливы соотношения
; .
Выражение в квадратных скобках является обобщенной силой, соответствующей первой обобщенной координате; учитывая соответствующее уравнение равновесия, получим для нее следующее выражение:
![]() .
.
Теперь дадим системе возможное перемещение по второй обобщенной координате, положив равным нулю возможное перемещение по первой обобщенной координате (т.е. ). Запишем для этого случая выражение суммы работ всех действующих на систему сил (так как груз и соосный блок остаются неподвижными, действующие на них силы работу не совершают). Вынесем за общую скобку. Тогда
 ,
,
где - возможное перемещение в точке приложения силы .
Запишем уравнения связей, используя соотношения кинематики:
;
![]() .
.
Для рассматриваемой механической системы возможные перемещения пропорциональны соответствующим скоростям, т.е. справедливо соотношение
.
Выражение в квадратных скобках является обобщенной силой, соответствующей первой обобщенной координате; учитывая соответствующее уравнение равновесия, получим для нее следующее выражение:
![]() .
.
Теперь составим выражение для кинетической энергии механической системы:
Запишем уравнения кинематических связей:
или ;
или .
Тогда выражение для кинетической энергии можно привести к виду
![]() .
.
При получении результата учтено, что осевой момент инерции однородного диска .
Продифференцировав выражение для кинетической энергии по обобщенным координатам, скоростям и по времени, получим слагаемые для левых частей уравнений Лагранжа второго рода:
![]()
![]()
![]()
![]()
![]() .
.
Подставим все полученные выражения в уравнения Лагранжа второго рода:
![]()
![]() .
.
Заметим, что система уравнений приводится к виду (22) при

![]()
![]()
![]()
![]()
![]()
Зная все обобщенные коэффициенты инерции и жесткости, составляем уравнение частот (25). Найдя его корни (частоты главных колебаний) и , по формулам (26) определяем коэффициенты форм главных колебаний и . Найденные значения позволяют записать выражения для законов изменения обобщенных координат в форме (28). Задание четырех начальных условий: при
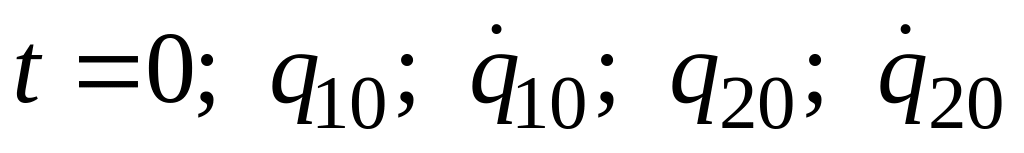 ,
позволяет определить четыре неизвестные
величины (
,
позволяет определить четыре неизвестные
величины (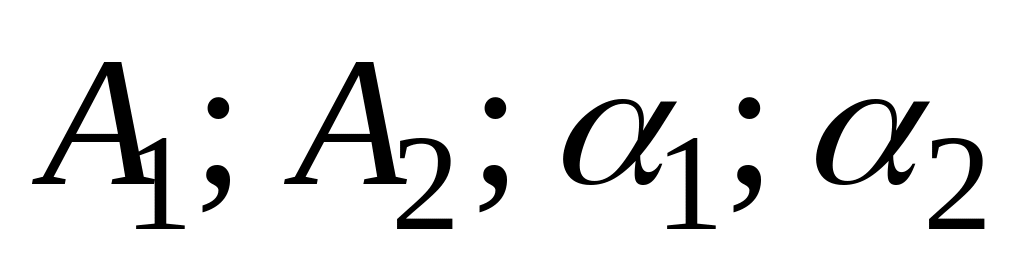 ),
содержащиеся в (28).
),
содержащиеся в (28).
