4.2. Примеры решения заданий

4.2.1. Положение равновесия линейной механической системы с одной степенью свободы

Механическая система, состоящая из груза, двух соосных (насаженных неподвижно на единую ось) блоков и диска, прикрепленных к земле пружиной и демпфером (см. Рис. 8), находится в положении статического равновесия. Зная жесткость пружины , веса груза и диска, а так же радиусы блоков и диска, определить удлинение пружины.

Рис. 8

РЕШЕНИЕ

1. Рассматриваемая механическая система обладает одной степенью свободы.

2. Заменим действие пружины силой упругости 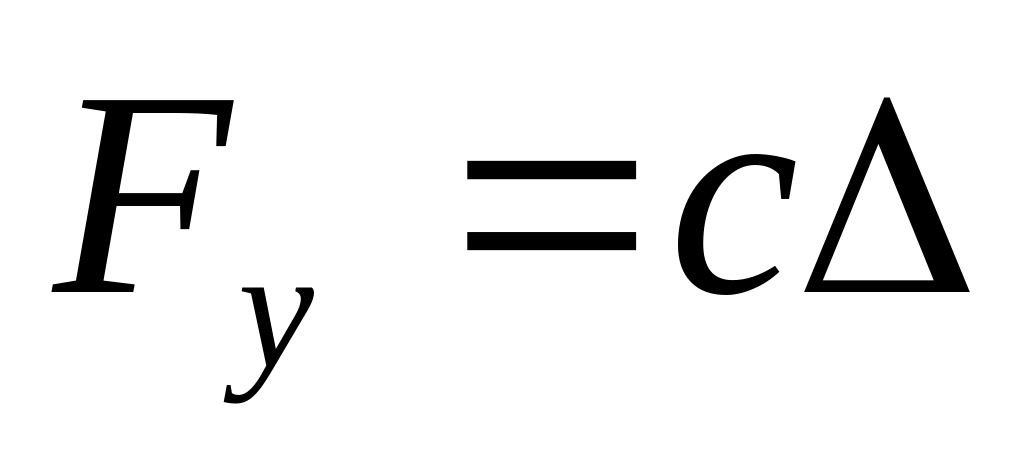, где - удлинение пружины в положении статического равновесия механической системы. Сила со стороны демпфера , пропорциональная скорости движения его поршня, при покое системы отсутствует.

3. Дадим системе возможное перемещение и запишем выражение для суммы работ всех действующих сил на возможных перемещениях точек их приложения; вынесем за общую скобку, сумму работ приравняем к нулю. Тогда

.

При получении выражения учтено, что элементарная работа силы равна нулю, так как сила приложена в мгновенном центре скоростей колеса 3.

4. Запишем уравнения связей, используя соотношения кинематики:

;

;

.

Для рассматриваемой механической системы возможные перемещения пропорциональны соответствующим скоростям, т.е. справедливы соотношения

; .

5. Приравняв нулю выражение в круглых скобках, получим выражение для расчета удлинения пружины в положении статического равновесия механической системы: .

4.2.2. Дифференциальное уравнение движения механической системы с одной степенью свободы

Используя уравнения Лагранжа второго рода получить дифференциальное уравнение движения груза. Осевой момент инерции соосных блоков и коэффициент силы сопротивления демпфера полагать заданным.

РЕШЕНИЕ

1. На Рис. 8 изображена механическая система и внешние силы, на нее действующие.

2. Выберем за обобщенную координату линейное перемещение первого груза. Уравнения кинематических связей останутся прежними:

или ;

или ;

или .

При записи учтено, что нити не растяжимы, а мгновенный центр скоростей диска, катящегося без скольжения, расположен в точке его соприкосновения с плоскостью.

3. Составим выражение для кинетической энергии механической системы:

.

4. Вынесем за скобки квадрат обобщенной скорости (скорости груза)

.

При получении результата учтено, что осевой момент инерции однородного диска .

5. Частная производная от кинетической энергии по обобщенной координате будет равна нулю, так как полученное выражение от обобщенной координаты не зависит.

Частная производная от кинетической энергии по обобщенной скорости будет

.

6. Производная по времени от частной производной кинетической энергии по обобщенной скорости будет

.

7. Для вычисления обобщенной силы дадим системе возможное перемещение. Составим сумму работ всех внешних сил на соответствующих возможных перемещениях и вынесем возможное перемещение по обобщенной координате 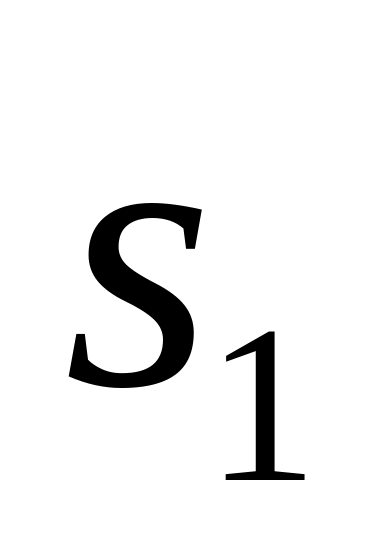за скобки:

Выражение в квадратных скобках и есть обобщенная сила для возможного перемещения по выбранной обобщенной координате (при записи учтено условие равновесия механической системы, полученное при решении предыдущего примера).

8. После подстановки в уравнения Лагранжа второго рода выражений для частных производных и обобщенной силы, окончательно имеем

.

Структура полученного уравнения совпадает с (16), решение которого обсуждено выше.

В случае необходимости определить законы движения других элементов механической системы следует воспользоваться уравнениями кинематических связей.